一种自动驾驶车辆自适应模型预测控制方法

本发明涉及自动驾驶车辆研究，具体地，涉及一种自动驾驶车辆自适应模型预测控制方法。

背景技术：

1、随着人们生活水平的不断提高，智能交通正受到越来越多的关注。自动驾驶技术在智能运输中发挥着重要作用。其中，车辆运动控制是自动驾驶技术的核心技术，在自动控制过程中确保车辆跟踪的准确性和稳定性是一个值得探索的问题。

2、车辆是一个复杂的系统，具有高度非线性的横向和纵向动态特性。考虑到高速自动驾驶车辆的行驶稳定性，道路环境变化和动力学参数的变化由于速度的提高，会严重影响车辆的行驶稳定性和安全性，同时会严重降低车辆轨迹跟踪的效果，甚至会导致自动驾驶车辆无法跟踪参考轨迹。采用复杂的控制器设计，虽然可以增强车辆行驶的稳定性，但实时性会受到严重影响。因此，如何在保证计算量，不降低实时性的情况下，进一步提高车辆的行驶安全性是值得研究的层面。

技术实现思路

1、针对现有技术中的缺陷，本发明的目的在于提供一种自动驾驶车辆自适应模型预测控制方法，提出预测水平函数，建立离线优化模型，时刻保证车辆的行驶状态最优。

2、为解决上述问题，本发明的技术方案为：

3、一种自动驾驶车辆自适应模型预测控制方法，包括以下步骤：

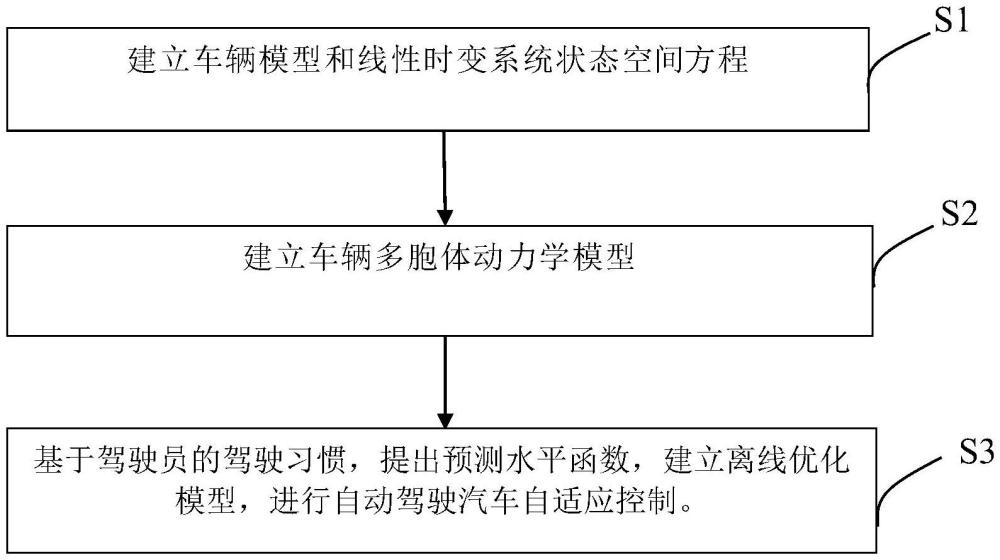
4、建立车辆模型和线性时变系统状态空间方程；

5、建立车辆多胞体动力学模型；

6、基于驾驶员的驾驶习惯，提出预测水平函数，建立离线优化模型，进行自动驾驶汽车自适应控制。

7、优选地，所述建立车辆模型和线性时变系统状态方程的步骤中，所述车辆模型包括车辆动力学模型和车辆跟踪误差模型，所述车辆动力学模型表示为：

8、

9、式中，m为车辆质量，

10、分别为车体质心处的纵向速度和侧向速度，δ为前轮转角，flf和flr为前后轮的纵向力，fxf和fxr为前后轮的侧向力，为横摆角速度，iz为车身绕z轴的转动惯量，lf、lr分别为车辆质心到前后轴的距离。

11、优选地，所述跟踪误差模型表示为：

12、

13、ey和分别为车辆的横向位置误差和航向角误差，κ是参考路径上的时变曲率。

14、优选地，所述建立车辆模型和线性时变系统状态方程的步骤中，所述建立线性时变系统状态空间方程为：选取将作为状态量，控制量为u＝δq，附加输入量λ＝[κ,s]t，状态空间形式为：

15、

16、将非线性汽车动力学模型线性化表示为：

17、

18、

19、其中，控制量δq是车辆前轮转角；κ为道路曲率；为车身横摆角；分别是横向位置和航向误差；和分别代表指标方向上的速度；和表示状态量和控制量分别与参考值的误差；车辆的基本参数m、iz、clf/clr和lf/lr分别代表车辆整备质量，车辆绕z轴的转动惯量，前/后轮胎的侧偏刚度、纵向刚度以及质心到前后轮的距离，mpc基于离散模型进行预测，对得到的进行前向欧拉离散化，对应每一个采样时刻状态空间形式为：

20、

21、ak,t＝ta+e bk,t＝tb dk,t＝td

22、其中t是采样时间。

23、优选地，所述建立车辆多胞体动力学模型的步骤具体包括：构建凸多胞体模型，考虑车辆不确定参数的影响，确定凸多胞体模型的顶点为23个，其中不确定参数取值范围分别为：

24、

25、采用控制增量的方法，建立新的状态空间方程为：

26、

27、

28、其中：

29、优选地，所述建立车辆多胞体动力学模型的步骤具体还包括：在一个预测时域的时长内，模型通过不断地迭代，进行预测，预测未来np个时刻的状态空间方程ξ，最终得出的输出方程为：

30、y(k)＝ψζ(k|t)+θδu(k)+γω(k)

31、

32、np为预测时域，nc为控制时域，δu1为控制增量。

33、优选地，所述基于驾驶员的驾驶习惯，提出预测水平函数，建立离线优化模型，进行自动驾驶汽车自适应控制的步骤，具体包括：基于驾驶员的驾驶习惯，从滚动优化底部逻辑进行分析，通过实验总结权重矩阵随步长变化的规律，提出预测水平函数，并采用改进的粒子群算法求出待定系数，从而在不增加控制器计算负担的前提下，针对环境变化改变控制器的集中度，从而进行自适应控制。

34、优选地，所述基于驾驶员的驾驶习惯，提出预测水平函数，建立离线优化模型，进行自动驾驶汽车自适应控制的步骤，具体包括：

35、权重随时域的变化规律总结；

36、基于驾驶员驾驶时，需要同时兼顾远处和近处的环境路况，但是更注重近距离短时间内的环境变化的驾驶习惯，对权重矩阵进行优化，将权重矩阵进行如下定义：

37、

38、式中：q1表示每一步优化目标函数输出项误差权重，i＝1,2…np；

39、离线模型的建立；

40、综合考虑道路曲率，运行车速，同时兼顾算法参数对轨迹跟踪性能、系统稳定性和计算效率的影响，在不改变预测时域的前提下，提出了一种自适应预测水平参数，并且通过离线优化多次迭代来调整待定系数，从而获得使计算时间和跟踪误差最小的，

41、

42、其中，f是权重变化方式的主导项；vk是k时刻的车辆纵向速度，κ,s道路曲率和滑移率；υ1,υ2,υ3,υ4,υ5和b是离线优化的待定系数；

43、根据水平预测函数建立离线参数优化模型：

44、

45、其中：因俩个目标函数不是相同数量级；所以引入k1,k2和s1,s2是比例因子，目标函数ft是单次滚动优化所需要的时间，fe是整个过程的跟踪误差，三个约束分别代表着单次滚动的计算时间不超过采样时间，由于权重矩阵中q一般会取很大的值，ωq在小范围内变化就会影响很大；

46、采用改进的粒子群算法，使其惯性权重可以随着算法的迭代自适应改变，

47、

48、其中为自适应惯性权重；favg为适应度的平均值；favg∈(fmax,fmin)；

49、以车身位置与质心侧偏角的跟踪误差值的积分值计算粒子的适应度：

50、

51、式中：fi(t)为粒子的适应度；将作为判断车辆行驶稳定性的评价指标，其分别为车辆跟踪全程的横向位置误差的积分值和质心侧偏角误差的积分值；ωp,ωβ分别作为车辆跟踪精度和稳定性俩个评价指标的权重，根据工况不同而变化。

52、优选地，所述基于驾驶员的驾驶习惯，提出预测水平函数，建立离线优化模型，进行自动驾驶汽车自适应控制的步骤，具体包括：

53、目标函数的建立；

54、为使得高速自动驾驶汽车有较高的跟踪精度，且能快速实现路径跟踪踪功能，需要选择合适的优化目标，建立目标函数，获得被控系统未来最优控制增量序列，基于多胞体动力学模型建立轨迹跟踪动力学优化指标：

55、

56、其中，y和yref为系统的输出预测值和参考值。为满足车辆可以在高速下实现良好的跟踪性能，在原有目标函数中加入了ey(k+i)和分别为k时刻的横向偏差和航向偏差，目的在于减小自动车辆实际跟踪轨迹与参考轨迹之间的偏差，提高车辆跟踪精度。qey和为位置误差权重系数；q和r为改进的权重矩阵；ε为松弛因子；

57、动态二次规划求解：

58、采用二次规划问题求解目标函数，把目标函数转化成形如下式的求解函数：

59、

60、s.t.az≤b,

61、lb≤z≤ub

62、其中，a，b为边界条件和约束条件构成的矩阵，lb,ub为控制增量阈值；通过求解把向量z中的第一个参数作为最优控制量传递给被控车辆执行，实现车辆在满足自身横向稳定性的同时能够安全的跟踪参考路径。

63、与现有技术相比，本发明的有益效果如下：

64、1、本发明提出了一种针对高速工况下的自适应模型预测控制的自动驾驶汽车轨迹跟踪的方法，在环境变化且内部外部存在扰动的时候，可以一定程度上消除扰动的影响，实现自动驾驶车辆安全行驶，并可以保持良好的轨迹跟踪效果以及保证车辆行驶的稳定性。

65、2、本发明基于驾驶员驾驶习惯，对权重系数改进，提出权重随时域变化的规律，有效提高了控制器的鲁棒性。

66、3、本发明考虑现实行驶工况下，环境和模型的变化，提出预测水平函数，采用改进的粒子群的方法，构建了一种基于模糊预测控制的权重系数实时调整策略，时刻保证车辆的行驶状态最优。