一种针对运行条件不断变化的自适应预测控制方法与流程

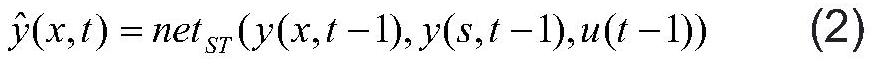
本发明涉及工业系统控制领域，特别是涉及一种针对运行条件不断变化的自适应预测控制方法。

背景技术：

1、随着工业技术的发展，工业系统变得越来越复杂化，这些系统的运行状态往往决定着生产的安全和效率，因此，保证其稳定高效运行十分重要。然而，这些系统运行机理复杂，通常具有非线性、时空耦合、无限维等特征，内部涉及多相、多场耦合，难以精准解析其内部的运行机理，从而无法维持其长期稳定运行，因此如何实现对工业系统的精准建模和稳定控制仍然是工业界和学术界一个重要的挑战。

2、针对工业系统，现有的建模控制方法主要分为集总式参数系统方法和分布式参数系统方法两类。集总式参数系统方法虽然可以在一定程度上实现对系统的建模和控制，但是这类方法并没有考虑系统状态的分布情况，无法使系统整体状态达到最优。而分布式参数系统方法虽然可以从物理场的角度对系统进行建模和控制，但是这类方法通常依赖已知的偏微分方程，工业现场缺乏相应的机理知识，难以满足这一条件。

3、随着大数据、传感器技术的发展，数据驱动的分布式参数系统建模方法出现，通过数据学习得到系统特征，但是这类方法通常采用批量处理的方式，当采集到新的数据时需要对历史数据和新数据重新进行训练以得到新模型，随着采集到的数据逐渐增多更新模型所需要的存储空间和计算时间也会成倍增长，导致这类方法难以应用到实际。为了解决数据存储和计算复杂度所带来的挑战，基于持续学习的建模方法被提出，这类方法利用新采集的数据在历史模型的基础上进行更新，仅需要处理新采集到的数据，可以显著降低数据存储量和模型计算复杂度。

4、然而上述持续学习方法在被应用到实际控制时仍然面临一些难题。首先，传统的持续学习方法通常假设工况变化时间提前已知，但是在实际控制中工况的变化往往无法提前已知，甚至某些工况的变化难以被准确识别。然后，分布式参数系统通常维数高，导致建立的预测模型计算复杂度高，使得难以实时准确预测，因此，如何实现具有新工况实时出现的多工况工业过程的稳定控制是一个具有挑战的问题。

技术实现思路

1、基于此，本发明的目的在于，提供一种针对运行条件不断变化的自适应预测控制方法，其具有准确识别工况变化，快速准确预测，实现全工况运行条件下的稳定控制的优点。

2、一种针对运行条件不断变化的自适应预测控制方法，具体步骤包括：

3、s1：提取系统的时空传递关系，构建基于时空特征的工况识别器，通过监测系统时空预测值和真实值之间的偏差，自动识别工况的变化，即工况识别机制；

4、s2：针对模型计算复杂度高的问题，运用时空分离的模型降阶方法，将高维模型降阶为空间基础函数和时间系数模型，实现并对分布式参数系统的快速预测，即模型在线更新机制；

5、s3：将s1的工况识别机制和s2的模型在线更新机制嵌入到模型预测控制框架中，通过对分布式参数系统的持续精准控制，实现全工况运行条件下的稳定控制。

6、本发明所述的针对运行条件不断变化的自适应预测控制方法，利用系统时空传递特征准确识别工况变化，并基于时空特征的工况识别方法，准确识别工况的变化并触发模型的更新；基于时空分离的模型更新方法，实现快速准确预测；最后，将工况识别机制和预测模型引入到预测控制框架中，从而实现全工况运行条件下的稳定控制。

7、进一步地，所述步骤s1中，在同一种工况参数下，系统的时空传递关系如下：

8、y(x,t)＝f(θ,y(x,t-1),y(s,t-1),u(t-1)) (1)

9、其中，f(·)表示系统的时空传递关系，s表示点x的临近点；

10、采用神经网络对其进行建模，表示如下：

11、

12、其中，netst(·)表示所构建的时空神经网络，反映系统在不同工况下的时空特征；

13、采用梯度下降法完成时空神经网络的训练，时空神经网络的预测输出和真实输出的具体偏差表达式如下：

14、

15、其中，y(x,t)表示在t时刻位置点x处的状态真实值，是计算得到的预测值，||·||2表示l2范数；采用kernel density estimation(kde)方法来构建工况识别的阈值，预测误差的概率密度函数的表达式如下：

16、

17、其中，m表示训练数据数量，h表示带宽，k(·)表示高斯核函数，当得到概率密度函数f(e)后，通过设置一个合适的置信度α得到阈值，具体计算表达式如下：

18、

19、求解公式(5)的积分上限得到阈值eth，该上限决定是否出现新的工况；通过以下公式判断系统工况：

20、

21、其中，lc(t)表示t时刻系统工况标签，s表示已知工况构成的标签集。

22、进一步地，所述步骤s2中，系统输出表示为y(x,t)被分解为无限维空间基础函数和对应的时间系数具体表达式如下：

23、

24、空间基础函数相互正交：

25、

26、时间系数计算公式如下：

27、

28、采用有限维的空间基础函数，具体表达式如下：

29、

30、其中，yn(x,t)表示y(x,t)的n阶近似，时空分解就被转化为最小化如下目标函数：

31、

32、采用拉格朗日乘子法，将公式(11)转变为如下形式：

33、

34、令得到：

35、

36、其中，表示为y(x,t)的线性组合：

37、

38、将公式(14)代入公式(13)可得：

39、

40、将公式(15)转换为矩阵形式：

41、

42、求解公式(16)得到对应的特征向量α1,…,αn，其中αi＝[αi1…αil]t，根据公式(14)构建空间基础函数

43、时间系数模型表示如下：

44、a(t)＝f(a(t-1),…,a(t-da),u(t-1),…,u(t-du))+e(t) (17)

45、其中，da和du是输入和输出滞后，e(t)表示偏差，a(t)＝[a1(t),…,an(t)]；函数f(·)通过低维数据辨识得到，采用神经网络模型进行表示，具体如下：

46、

47、通过上述步骤实现对时间系数的预测，再结合得到的空间基础函数，重构得到系统输出的预测值

48、

49、进一步地，所述步骤s3中，运用滚动优化并基于在线预测结果，通过在线优化找到合适的控制输入使得系统输出能够快速跟踪到控制目标，其中优化问题表示为如下形式：

50、

51、其中表示控制目标，表示预测值，表示通过时间系数预测模型得到的时间系数预测值，通过时空重构得到系统预测输出；表示第mp步的预测值属于安全集；u(t)表示t时刻系统控制输入；mp和mc分别表示预测步长和控制步长，q和p表示权重参数矩阵。

52、为了更好地理解和实施，下面结合附图详细说明本发明。