一种考虑能源SOC变化的机电执行机构控制方法

本发明涉及机电执行机构控制领域，特别是一种考虑能源soc变化的机电执行机构控制方法。

背景技术：

1、机电伺服系统作为多学科综合的自动化装置，被广泛地应用于各类领域。实际中，完整的伺服系统包含了伺服机构以及为伺服机构运行提供动力源的伺服能源，在航空航天领域，蓄电池是伺服能源的主要类型之一。比如运载火箭的电动舵面伺服系统，卫星控制力矩陀螺或反作用轮等，均是依靠蓄电池驱动的伺服系统，能源与伺服机构构成了一个具有较强耦合关系的非线性快速时变系统。伺服电机快速启停引起的电压波动，机械负载的不确定性扰动，电池参数的变化、寿命的衰减等因素都会对伺服系统的工作性能造成影响。

2、现有的研究多将伺服机构与其能源分开考虑，局限于伺服机构本身控制算法的改进与提升，忽略了能源是影响伺服系统控制效能的重要因素之一。对于大量采用电池供电的伺服机构来说，传统控制方法只考虑伺服机构本身控制，而且由于无法实时获知能源状态的变化，导致无法根据能源状态的改变及时做出控制补偿，进而会造成系统性能的损失。

3、伺服能源与伺服机构的控制是相互耦合相互影响的，为了提升机电伺服系统的控制性能，提高伺服能源利用效率，有必要从系统角度出发，建立考虑能源特性的伺服系统全局模型并开展考虑能源变化的优化控制方法研究，最大程度发挥伺服系统的控制潜力。

技术实现思路

1、本发明针对传统伺服系统控制方法只考虑伺服机构本身控制，忽略了伺服能源对伺服机构控制的耦合作用，无法根据能源状态的改变及时做出控制补偿，造成系统性能损失的问题，提出了一种考虑能源soc变化的机电执行机构控制方法，以降低电池电量变化对伺服机构控制性能造成的不利影响。

2、本发明的技术方案为：

3、所述一种考虑能源soc变化的机电执行机构控制方法，包括以下步骤：

4、步骤1：建立包含伺服能源的伺服系统模型；

5、步骤2：对伺服能源的soc状态量进行估计；

6、步骤3：在准比例谐振控制器上并联增加一个积分环节，得到改进的准比例谐振控制器；所述改进的准比例谐振控制器能够无静差跟踪直流信号；

7、步骤4：将改进的准比例谐振控制器与模糊控制器相结合，得到考虑锂电池soc的模糊改进准比例谐振控制器，实现伺服机构的角度闭环控制；

8、所述模糊改进准比例谐振控制器中的各个系数由整定系数和修正系数叠加得到，其中修正系数由步骤2估计得到的soc状态量以及伺服系统角度误差e及其导数ec的乘积e·ec作为模糊输入变量，通过模糊推理得到。

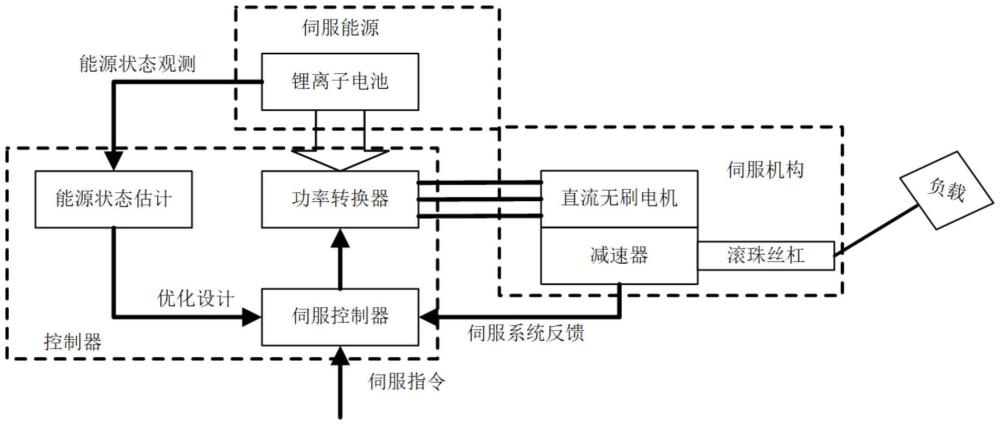
9、进一步的，步骤1中，伺服系统包括伺服机构、伺服能源以及控制器；

10、对于伺服机构，根据伺服机构特性建立模型，分别得到角度、电流与驱动电压的传递函数表达式；

11、对于伺服能源，根据伺服能源特性构建二阶rc等效电路模型。

12、进一步的，步骤1中，角度与驱动电压，电流与驱动电压的传递函数为：

13、

14、其中k1,k2,k3,k4分别为设定系数。

15、进一步的，步骤1中，角度与驱动电压以及电流与驱动电压的传递函数通过对伺服机构数学模型进行拉普拉斯变换得到，所述伺服机构数学模型为：

16、

17、其中ω为电机输出轴的转动角速度；ubat为电机驱动电压；te为电机电磁转矩；i为电机电枢电流；tl为负载转矩；l为电机电枢电感；b为摩擦转矩系数；r为电机电枢电阻；j为伺服系统转动惯量；kt为电机转矩系数；ke为电机反电动势系数；k为减速比；θ为经过减速器后的电机输出轴转动角度；kl为负载力矩系数。

18、进一步的，角度与驱动电压以及电流与驱动电压的传递函数中，设定系数k1,k2,k3,k4取：

19、k1＝jl；k2＝bl+jr；k3＝kkll+br+ktke；k4＝kklr。

20、进一步的，步骤1中，伺服能源为锂电池，锂电池的数学模型为

21、

22、其中uocv为电池开路电压；i为电池输出电流，规定电流流入电池为负，流出电池为正；rohm为电池内阻；ut为电池输出电压；soc0为初始时刻soc值；q0为电池额定容量；uc为锂电池浓差极化效应电压；ud为锂电池扩散极化效应电压；rc为锂离子电池浓差极化效应产生的电阻；cc为锂离子电池浓差极化效应产生的电容；rd为锂离子电池扩散极化效应产生的电阻；cd为锂离子电池扩散极化效应产生的电容；f(soct)表示uocv与soc的非线性函数关系。

23、进一步的，步骤1中，锂电池的数学模型转化为状态方程的形式后得到锂电池状态空间表达式：

24、

25、式中：

26、x＝[uc ud soc]t；

27、

28、

29、c＝[-1 -1 ]；

30、τc＝rccc；

31、τd＝rdcd。

32、进一步的，步骤2中，根据锂电池状态空间表达式，对电池soc状态量设计扩展卡尔曼观测器，对锂电池soc进行估计。

33、进一步的，步骤4中，考虑锂电池soc的模糊改进准比例谐振控制器为：

34、

35、其中kp'为整定的比例系数；kr'为整定的谐振系数；ki'为整定的积分系数；δkp为模糊控制修正的比例系数；δkr为模糊控制修正的谐振系数；δki为模糊控制修正的积分系数。

36、进一步的，步骤4中，模糊推理的输入变量为：步骤2得到的锂电池soc的扩展卡尔曼滤波估计值、伺服系统的角度误差e及其导数ec的乘积e·ec；输出变量为：δkp、δkr和δki。

37、有益效果

38、本发明提出的模糊改进准pr控制方法，相较于传统pid控制而言，在面对电池能量变化以及外界干扰等不确定性的因素时，具有如下效果：

39、1)在低电量的情况下，针对脉冲及周期性力矩干扰具有更好的鲁棒性；

40、当soc为0.25时，在t＝2.5s处，对伺服机构负载端分别引入脉冲干扰力矩以及周期性干扰力矩。进行仿真实验，角度相应曲线如图1、图2所示。

41、图1所示为脉冲干扰力矩为0.1nm时的角度响应曲线，角度跟踪误差最大值与重新收敛时间如表1所示。分析可得，在负载端施加脉冲干扰力矩之后，pid控制器作用下输出角度波动的最大值为0.108°，重新收敛时间为70ms；改进准pr控制器作用下输出角度波动的最大值为0.023°，重新收敛时间为25ms；模糊改进准pr控制器作用下输出角度波动的最大值为0.015°，重新收敛时间为21ms。

42、由此可以看出，当伺服系统在低电量运行时，在引入脉冲干扰力矩后，模糊改进准pr控制可以在很短的时间内更好地克服力矩干扰，具备更强的抗干扰性能。

43、表1脉冲干扰力矩下角度跟踪误差与收敛时间

44、

45、图2所示为周期性干扰力矩为d1＝0.05sin(10t+4.74)+0.02时的角度响应曲线，仿真跟踪误差情况如表2所示。分析可得，在负载端施加周期性干扰力矩之后，pid控制器作用下输出角度已经出现周期性变化，角度波动的最大值为0.195°,平均值为0.001°；改进准pr控制器仍可以较好地跟踪角度响应曲线，角度的波动最大值为0.021°，平均值为0.003°；而模糊改进准pr控制器作用下输出角度基本与给定角度曲线重合，角度的波动最大值为0.003°，平均值为0.001°。

46、仿真结果表明，当伺服系统在低电量运行时，在引入周期性干扰力矩后，pid控制已经不能很好地跟踪给定角度。而模糊改进准pr控制相较于改进准pr控制而言，最大值与平均值均更小。证明本文设计的模糊改进准pr控制在周期性的干扰力矩作用下仍能保持较好的跟踪性能。

47、表2周期干扰力矩下跟踪误差情况

48、

49、2)具有更好的性能以及电池能量变化对其控制性能的影响较小。

50、选取上升时间，最大速度以及带宽作为衡量指标。以0.1为间隔对soc在1～0.2区间开展仿真，并将仿真数据利用最小二乘法进行拟合。结果曲线如图3、图4、图5所示。从图中可以看出，在pid控制策略作用下，伺服系统上升时间为32ms，最大转速为320°/s，带宽为18.3hz；在改进准pr控制策略作用下，伺服系统上升时间为17ms，最大转速为345°/s，带宽为21.9hz；而模糊改进准pr控制策略作用下，伺服系统上升时间为15ms，最大转速为350°/s，带宽为29.6hz。

51、从仿真结果可以看出，由于模糊改进准pr控制将伺服能源soc作为模糊输入变量之一，对伺服系统的时域性能提升效果更好，且对soc变化具有更强的鲁棒性。

52、本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。