针对无人机的数据处理系统、方法、装置及存储介质

本技术涉及数据处理领域，特别是涉及一种针对无人机的数据处理系统、方法、装置及存储介质。

背景技术：

1、近年来，随着人工智能、传感器以及控制算法等技术的不断创新与发展，四旋翼无人机逐渐成为了二十一世纪智能科技的一大热点话题。四旋翼无人机凭借着其结构简单、机动性强、垂直起降、自主悬停、易于操作等特点，被广泛应用于军事侦察、农业灌溉、搜索救援等领域。

2、对于四旋翼无人机来说，一个良好的飞行运动控制算法是四旋翼无人机完成飞行任务的关键。目前，无论是在农业灌溉还是搜索救援领域，四旋翼无人机在执行飞行任务时，往往都是需要精确地跟踪上事先规划好的路径点或者轨迹，但是要想实现四旋翼无人机的飞行运动控制并跟踪既定的轨迹仍然存在较大的困难。首先，四旋翼无人机是一个典型的多输入多输出的欠驱动非线性系统，各个输入输出之间都存在着强烈的耦合关系；其次，四旋翼无人机易受外界环境的干扰，无法建立精确的动力学模型。而一个良好的控制算法直接决定了四旋翼无人机在飞行过程中跟踪轨迹的性能，所以四旋翼无人机的控制算法设计具有重要的研究意义。

3、目前，pid仍然是四旋翼无人机在实际应用中使用最广泛的控制算法，虽然它的设计不依赖于四旋翼无人机的运动学和动力学模型，在模型建立方面能减少一定的工作量，但是pid控制器通常只适用于单一的输入输出线性系统，对于四旋翼无人机这种多输入多输出强耦合的非线性复杂系统，在复杂环境下执行轨迹跟踪任务时，pid的跟踪性能也是不尽人意。而对于如今研究较为热门的线性二次型调节（linear quadratic regulator，lqr）、滑模控制（sliding model control，smc）、自抗扰控制（active disturbancerejection control, adrc）这几类控制器而言，相比于传统的pid，在稳定性和准确性上有一定的提高，但是在预测四旋翼无人机系统未来行为的能力上有所不足，无法提前采取措施来避免飞行过程中存在的潜在问题；此外，这几类控制器也无法处理约束问题，无法有效地约束四旋翼无人机的状态量和控制量，从而无法避免无人机在飞行过程中因速度或角度过大导致坠机的问题。为此，也有研究人员提出将模型预测控制算法应用在四旋翼无人机上，但是，大部分的研究都是如何提高控制器的鲁棒性以及轨迹跟踪的准确性，而忽略了求解优化过程中的庞大计算量，现有的模型预测控制方法在实时求解由二次规划问题的最优解的过程中，都是利用传统的二次规划序列求解方法，此类方法需要进行复杂的矩阵逆运算，求偏导等过程，计算量很大，不适用于实时求解四旋翼无人机在轨迹跟踪每个采样时刻的最优控制输入。

4、基于此，一种大幅度减少计算复杂度，提高计算效率的无人机数据处理系统亟待研发。

技术实现思路

1、本技术针对现有技术的不足， 提出了一种基于神经网络优化和模型预测控制相结合的无人机的数据处理系统、方法及装置。

2、本技术解决上述技术问题所采取的技术方案是：

3、一种针对无人机的数据处理系统，包括：

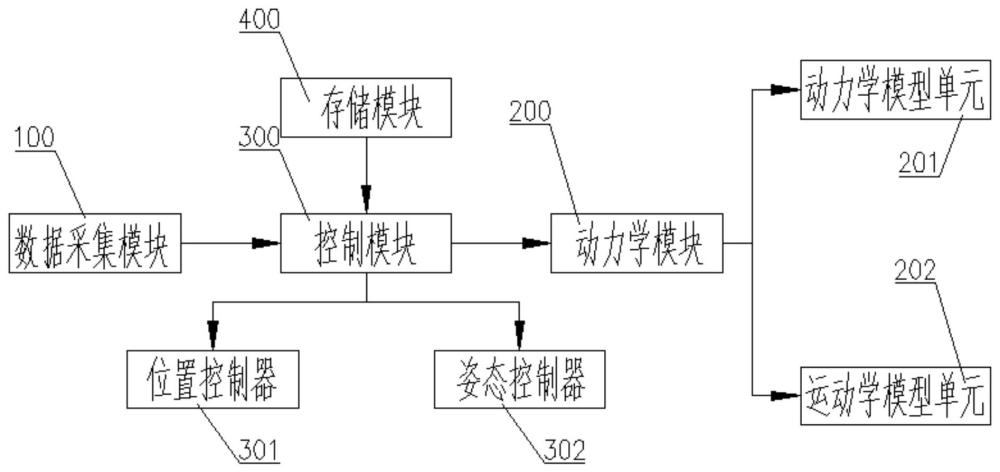
4、数据采集模块，用于采集无人机的参考位姿和实际位姿数据；

5、存储模块，用于存储无人机的动力学模型和运动学模型；

6、动力学模块，用于计算得到无人机的实际位姿数据，将数据传输给数据采集模块，并根据最优控制量数据对无人机的参考轨迹进行跟踪控制；

7、控制模块，设置在所述数据采集模块与动力学模块之间，并同时与所述数据采集模块、所述动力学模块进行数据交互，用于根据无人机的所述运动学模型与所述动力学模型，构建带有状态量和控制量约束的模型预测控制的代价函数，并将所述代价函数转化为带有约束的二次规划问题，再通过原始对偶神经网络求解所述带有约束的二次规划问题，以输出所述的最优控制量数据。

8、所述控制模块，包括：

9、位置控制器，与所述采集模块连接，用于根据实际位姿和参考位姿数据输出最优控制量数据中的升力数据；

10、姿态控制器，与所述数据采集模块连接，用于根据实际位姿和参考位姿数据输出最优控制量数据中的三轴力矩数据；

11、所述动力学模块，包括：

12、动力学模型单元，与所述位置控制器、所述姿态控制器连接，用于根据所述最优控制量数据利用动力学模型输出实际线速度数据以及实际角速度数据；

13、运动学模型单元，与所述动力学模型单元的输出端连接，用于根据所述实际线速度数据以及实际角速度数据利用运动学模型得到无人机实际位置信息以及实际姿态角数据；

14、所述位置控制器与所述运动学模型单元的输出端连接，用于获取所述无人机实际位置信息；

15、所述姿态控制器与所述运动学模型单元的输出端连接，用于获取所述实际姿态角数据。

16、所述根据无人机的所述运动学模型与所述动力学模型，构建带有状态量和控制量约束的模型预测控制的代价函数，包括：

17、将无人机的模型进行离散化处理，得到离散化后的状态空间方程，不进行解耦操作；

18、将所述离散化后的状态空间方程中的预测时域等于控制时域，构建出带有状态约束和控制约束的代价函数以及预测模型状态方程。

19、所述将无人机的模型进行离散化处理，得到离散化后的状态空间方程，不进行解耦操作，包括：

20、将无人机的动力学和运动学模型进行离散化处理，得到离散时间下的状态空间方程：；

21、式中<mi>ς=[x,y,z,</mi><mover><mi>x</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>y</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>z</mi><mo stretchy="true">̇</mo></mover><mi>,ϕ,θ,ψ,</mi><mover><mi>ϕ</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>θ</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>ψ</mi><mo stretchy="true">̇</mo></mover><msup><mi>]</mi><mi>t</mi></msup>表示实际的状态输入量，其中分别表示三个方向的坐标位置，分别表示三个方向上的速度，分别表示翻滚角、俯仰角、偏航角，分别表示翻滚角、俯仰角、偏航角的角速度；<mi>u=[</mi><msub><mi>u</mi><mn>1</mn></msub><mi>,</mi><msub><mi>u</mi><mn>2</mn></msub><mi>,</mi><msub><mi>u</mi><mn>3</mn></msub><mi>,</mi><msub><mi>u</mi><mn>4</mn></msub><msup><mi>]</mi><mi>t</mi></msup>表示控制输入量，其中，，，表示合升力，分别表示三个方向上的力矩；<mi>y=[x,y,z,ψ</mi><msup><mi>]</mi><mi>t</mi></msup>表示状态输出量；表示离散时间；表示状态输入系数矩阵，表示控制输入系数矩阵，表示状态输出系数矩阵；

22、其中，表示单位阵，表示的零矩阵，表示采样时间，，；分别表示三个方向上的转动惯量。

23、对所述离散化后的状态空间方程进行处理，构建出带有状态约束和控制约束的代价函数和预测模型状态方程。

24、所述对所述离散化后的状态空间方程进行处理，构建出带有状态约束和控制约束的代价函数和预测模型状态方程，包括：

25、将所述离散化后的状态空间方程中的预测时域等于控制时域，且步长为，则所述带有状态约束和控制约束的代价函数为：

26、；

27、其中，<mi>ς=</mi><mi>[x,y,z,</mi><mover><mi>x</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>y</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>z</mi><mo stretchy="true">̇</mo></mover><mi>,ϕ,θ,ψ,</mi><mover><mi>ϕ</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>θ</mi><mo stretchy="true">̇</mo></mover><mi>,</mi><mover><mi>ψ</mi><mo stretchy="true">̇</mo></mover><msup><mi>]</mi><mi>t</mi></msup>表示实际的状态输入量；<msub><mi>ς</mi><mi>ref</mi></msub><mi>=[</mi><msub><mi>x</mi><mi>r</mi></msub><mi>,</mi><msub><mi>y</mi><mi>r</mi></msub><mi>,</mi><msub><mi>z</mi><mi>r</mi></msub><mi>,</mi><msub><mover><mi>x</mi><mo stretchy="true">̇</mo></mover><mi>r</mi></msub><mi>,</mi><msub><mover><mi>y</mi><mo stretchy="true">̇</mo></mover><mi>r</mi></msub><mi>,</mi><msub><mover><mi>z</mi><mo stretchy="true">̇</mo></mover><mi>r</mi></msub><mi>,</mi><msub><mi>ϕ</mi><mi>r</mi></msub><mi>,</mi><msub><mi>θ</mi><mi>r</mi></msub><mi>,</mi><msub><mi>ψ</mi><mi>r</mi></msub><mi>,</mi><msub><mover><mi>ϕ</mi><mo stretchy="true">̇</mo></mover><mi>r</mi></msub><mi>,</mi><msub><mover><mi>θ</mi><mo stretchy="true">̇</mo></mover><mi>r</mi></msub><mi>,</mi><msub><mover><mi>ψ</mi><mo stretchy="true">̇</mo></mover><mi>r</mi></msub><msup><mi>]</mi><mi>t</mi></msup>表示参考的状态输入量，表示控制量；q表示状态权重矩阵，r表示控制权重矩阵；k表示离散时间;表示状态量的最小值；表示状态量的最大值；表示控制量的最大值；表示控制量的最小值。

28、根据模型预测控制的预测未来行为的能力，可以得到系统的预测模型状态方程以及对应的状态约束和控制约束分别为：；；

29、其中，；其中，表示状态输入系数矩阵，表示控制输入系数矩阵，表示控制时域，等于预测时域的时间步长；，，，。

30、所述将所述代价函数转化为带有约束的二次规划问题，再通过原始对偶神经网络求解所述带有约束的二次规划问题，包括：

31、所述的代价函数为：

32、；

33、将所述代价函数转化为带有状态约束和控制约束的二次规划问题，为：，；

34、其中，，

35、；表示状态输出系数矩阵；q表示状态权重矩阵，r表示控制权重矩阵； n表示控制时域或者预测时域的时间步长；

36、利用原始对偶神经网络来求解所述带有状态约束和控制约束的二次规划问题：

37、定义原始对偶决策向量和上下界向量如下：，；其中，表示原始对偶决策向量，表示上界向量，表示下界向量，表示相关的对偶决策向量；为对偶决策向量上界向量；为对偶决策向量下界向量；表示预测模型状态方程中的预测控制向量；表示预测控制向量的最小值；表示预测控制向量的最大值。 根据二次规划问题中的矩阵,建立原始对偶神经网络的动力学微分方程，得到： ；

38、其中，，，表示单位阵，表示原始对偶神经网络收敛率；是关于原始对偶决策向量的限幅函数；

39、利用龙格库塔法来求解原始对偶神经网络动力学微分方程，构建如下的四阶龙格库塔方程：

40、

41、 ；

42、其中，表示时间步长，表示阶泰勒展开式，表示原始对偶神经网络的动力学微分方程的最优解；通过求解上述的四阶龙格库塔方程便能得到原始对偶神经网络的动力学微分方程的最优解，中的前个元素即为所设计的控制器每个采样时刻的最优控制量。

43、一种如上所述的针对无人机的数据处理系统的无人机控制方法，包括：

44、采集无人机的实际位姿数据和参考位姿数据；

45、构建无人机的运动学模型与动力学模型；

46、根据无人机的所述运动学模型与所述动力学模型，构建带有状态量和控制量约束的模型预测控制的代价函数；

47、将所述代价函数转化为带有约束的二次规划问题；

48、通过原始对偶神经网络求解所述带有约束的二次规划问题，以输出所述的最优控制量数据。

49、一种用于数据处理的电子装置，包括：

50、存储介质，用于存储计算机程序；

51、处理单元，与所述存储介质进行数据交换，用于在处理针对无人机的数据时，通过所述处理单元执行所述计算机程序，进行如上所述的方法的步骤。

52、一种计算机可读存储介质，其特征在于：

53、所述计算机可读存储介质内存储有计算机程序；

54、所述计算机程序在运行时，执行如上所述的方法的步骤。

55、本技术所带来的有益效果为：

56、本技术所述的系统，利用数据采集模块采集无人机的参考位姿数据，获取无人机的实际位姿数据，并根据最优控制量数据对无人机的轨迹进行跟踪控制；通过控制模块根据无人机的所述运动学模型与所述动力学模型，构建带有状态量和控制量约束的模型预测控制的代价函数，并将所述代价函数转化为带有约束的二次规划问题，再通过原始对偶神经网络求解所述带有约束的二次规划问题，以输出所述的最优控制量数据。

57、本技术所述的系统，相比于传统的pid控制，完全适用于四旋翼无人机这种多输入多输出、强耦合的非线性复杂系统，能够有效提高四旋翼无人机轨迹跟踪控制的精确性、稳定性；相比于lqr、smc、ardc这几类控制器，本技术所述的系统具有更强的预测四旋翼无人机系统未来的能力，同时还能够处理多约束问题，以此来提高四旋翼无人机飞行过程中的安全性；相比于现有的模型预测控制，本技术所述的系统提出利用原始对偶神经网络来实时求解模型预测控制所构成的二次规划问题，大大地减少了计算的复杂度，提高了计算效率。