网络时延四旋翼无人机多速率采样IQC控制方法

本发明涉及四旋翼无人机多速率采样控制，具体属于一种网络时延四旋翼无人机多速率采样iqc控制方法。

背景技术：

1、四旋翼无人机通过控制四个旋翼的速度和转向来实现姿态、速度和位置的变化，具有比固定翼无人机更灵活、更安全的优点。然而，由于四旋翼无人机需要通过四个独立的控制输入来控制六个自由度的输出，因此它的控制是困难的。四旋翼无人机的研究需要在保证无线装置四旋翼有效控制的同时，处理模型中的强耦合动力学，这对模型分析提出了重大挑战。针对这一问题，非线性鲁棒控制方法具有较高的计算复杂度。为此，反馈线性化方法可以有效地简化模型，从而发挥线性系统控制器设计方法的优势。在网络控制系统中，尽管有些系统具有连续时间动力学，但控制器通常是离散时间的。因此，同时包含连续时间系统和数字控制器的采样控制系统得到了广泛的研究。成熟的采样数据控制器设计方法有很多，例如切换系统法、随机系统法、混合系统法、李雅普诺夫泛函法、输入延迟法等。

2、与单速率采样控制相比，多传感器的多速率采样控制考虑到不同信道对系统控制效果有不同程度的影响，更具资源效率和灵活性。多控制回路多速率采样控制用于四旋翼无人机的轨迹跟踪控制，如果考虑所构建的李雅普诺夫函数过于复杂，这增加了计算复杂度。而pid控制作为一种经典的控制方法，在工业控制中得到了广泛的应用，其中针对四旋翼无人机的轨迹跟踪方案研究了多速率采样数据pid控制方法，但该方法的精度依赖于参数的调整，这一般需要一定的经验。此外，在研究网络控制系统时，必须考虑网络引起的一系列网络诱发问题，其中网络诱发延迟和时变采样数据间隔是最基本的问题。在许多研究中，积分二次约束（iqc）框架可以大大降低计算复杂度，为不确定时延系统的稳定性分析提供了一种简单的方法。但是控制器的设计会引入大量的非线性项，如何让处理非线性项，会直接影响控制效果。

技术实现思路

1、为解决网络时延四旋翼无人机控制的技术问题，本发明提出了一种网络时延四旋翼无人机多速率采样iqc控制方法，从而大大简化了模型处理过程，降低了计算复杂度，实现了对四旋翼无人机目标轨迹的跟踪控制。

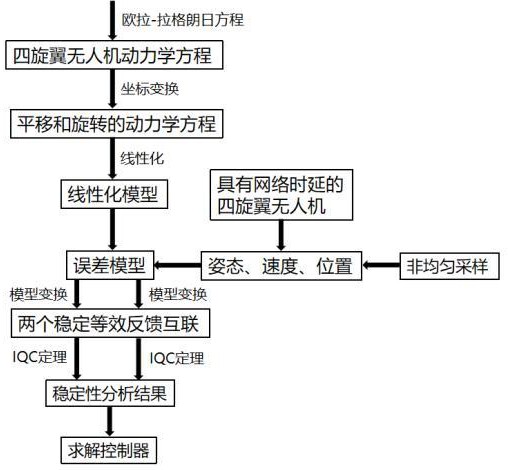
2、本发明所提供的一种网络时延四旋翼无人机多速率采样iqc控制方法，其特征在于，包括以下步骤，

3、步骤1，建立四旋翼无人机平移和旋转的动力学方程；

4、步骤2，通过研究四旋翼无人机处于悬停状态时的目标轨迹跟踪控制，结合线性化过程给出线性化模型；

5、步骤3，考虑采样控制中存在时间延迟，给出采样下关于误差的控制输入，进而将线性化模型转化为误差模型；

6、步骤4，构造算子引入指数衰减率，通过模型变换，将误差模型转化为反馈互联；

7、步骤5，在积分二次约束框架下，给出了四旋翼无人机悬停状态的稳定性条件，进而降低计算复杂度；

8、步骤6，求解基于积分二次约束和锥补线性化算法的网络时延四旋翼无人机多速率采样控制器增益矩阵。

9、进一步的，在步骤1中，四旋翼无人机在惯性参考系中有6个自由度，即沿、、轴的位置变量、、，以及用欧拉角表示的旋转角度、、，四旋翼无人机通过改变第个螺旋桨产生的升力，，通过电机发出相应的速度指令调整姿态、速度和位置，通过改变升力，完成各种运动，包括滚转和俯仰运动；

10、令，，四旋翼无人机的平移动能表示为，旋转动能表示为，势能表示为，拉格朗日模型表示为

11、

12、其中是转动惯量矩阵；

13、根据欧拉-拉格朗日方程，将四旋翼动力学方程写成

14、

15、其中是由于控制输入而施加到四旋翼的平移力，是包含滚转、俯仰和偏航力矩的向量；

16、根据坐标变换，得到四旋翼无人机平移和旋转的动力学方程联立为，

17、（1）

18、其中，表示四旋翼的质量，表示重力加速度，、、表示沿着、、轴的转动惯量矩阵，、、、是控制输入的分量，以及，而、、、是螺旋桨的旋转速度，且

19、。

20、进一步的，在步骤2中，基于悬停状态的稳定性，进而考虑四旋翼无人机处于悬停状态仍是稳定的目标轨迹跟踪，将四旋翼无人机控制输入表示为

21、

22、状态向量表示为

23、

24、结合线性化过程得到如下线性化模型

25、 （2）

26、其中，和为系统参数矩阵，即

27、。

28、进一步的，在步骤3中，在姿态、速度和位置三个控制回路的多速率采样控制中，三个回路分别以姿态向量，速度向量，位置向量为状态向量，采样后的信号转换为数字信号，通过离散时间控制器提供给执行器，并由零阶保持器保存为连续时间信号；

29、将姿态控制回路记为第1个控制回路，速度控制回路记为第2个控制回路，位置控制回路记为第3个控制回路，将在第个控制回路中的采样数据时刻集记为，，并满足；由于时延的影响，在第个控制回路中，时刻的采样数据信号在离散时间控制器动作后直到时刻才传输到执行器，传输延迟记为，满足；

30、因此，采样下关于误差的控制输入相应表示为

31、（3）

32、其中，是参考状态向量，是采样下的状态向量，是采样下的参考状态向量，是基于积分二次约束和锥补线性化算法的网络时延四旋翼无人机多速率采样控制器增益矩阵，是姿态控制器，是速度控制器，是位置控制器，从而得到

33、

34、令误差向量为，采样下的误差向量为，并对控制输入（3）进行积分计算，将线性化模型（2）转化为与误差相关的模型，表示为

35、（4）。

36、进一步的，在步骤4中，构造算子、、，令，通过模型变换，将与误差相关的模型（4）表示为如下所示的稳定的等效反馈互联

37、（5）

38、和（6）

39、其中，指数衰减率为，与均为初始值，且

40、。

41、进一步的，在步骤5中，以等效反馈互联（5）和（6）为基础，基于积分二次约束定理，在矩阵是赫尔维茨矩阵的情况下，对于给定，存在对称正定矩阵、、、、、，使得

42、（7）

43、成立，则线性化模型（2）是指数稳定的，其中，，，，

44、在是赫尔维茨矩阵的情况下，给定，，，存在矩阵，对称正定矩阵、、、、、、、、、、、、、、，其中，使得下面的不等式（9）-不等式（13）在优化约束下成立，那么在姿态、速度和位置三个控制回路的多速率采样控制下的线性化模型（2）指数稳定；控制器增益矩阵由得到；限制表示为

45、（8）

46、使得

47、（9）

48、（10）

49、（11）

50、（12）

51、（13）

52、其中，，，，，，，。

53、进一步的，在步骤6中，首先导出具有一定保守性的初始控制器，然后通过迭代逐渐降低保守性；当姿态、速度和位置三个控制回路以相同速率采样时，将变量的条件替换为，将的条件替换为，将的条件替换为；

54、给定采样区间和延迟区间，，且令；控制器增益矩阵为；计算方法如下，

55、a.求解变量变换、、下的最小化问题

56、（14）；

57、b.标记最优解，，；

58、c.通过、、求解最小化问题（14）；

59、d.求解最优解，，，令

60、，；

61、e.当 且是赫尔维茨矩阵，重复步骤c-e；反之执行步骤f；

62、f.结束循环，输出基于积分二次约束和锥补线性化算法的网络时延四旋翼无人机多速率采样控制器增益矩阵。

63、本发明所提供的一种网络时延四旋翼无人机多速率采样iqc控制方法，基于具有任意网络时延的四旋翼无人机在姿态、速度和位置三个控制回路下的稳定性分析和目标轨迹跟踪问题，考虑多速率采样数据控制，在不同采样频率下对姿态、速度和位置三个控制回路进行非均匀采样；通过模型变换将四旋翼无人机在任意点悬停问题转化为非零平衡点的稳定性分析问题；分析构建的误差模型，实现目标轨迹的跟踪控制；最后求解出基于积分二次约束和锥补线性化算法的网络时延四旋翼无人机多速率采样控制器增益矩阵。综上所述，本发明具有以下有益效果，

64、1.本发明采用反馈线性化的方法处理非线性元素，为了节省更多的资源，实现更灵活的控制，采用基于积分二次约束的多速率采样控制，分别在不同频率下对姿态回路、速度回路和位置回路进行非均匀采样；

65、2.本发明在积分二次约束框架下进行模型转换构建误差模型，将四旋翼飞行器在任一点悬停的稳定性问题转化为误差模型非零平衡点的稳定性分析问题，将目标轨迹的跟踪控制问题转化为误差模型的镇定问题，实现了四旋翼无人机的稳定性评估和目标轨迹的跟踪控制。