非线性电机伺服系统的最优轨迹跟踪控制方法及装置

本技术涉及控制理论，尤其涉及非线性电机伺服系统的最优轨迹跟踪控制方法及装置。

背景技术：

1、轨迹跟踪控制旨在设计控制策略，使受控系统能够跟踪预定义的轨迹。传统的控制方法，如pid控制器等，依赖于对系统的精确建模和参数设定。然而，实际系统通常具有复杂的动态特性，例如非线性等，这使得传统方法往往难以达到理想的跟踪性能。最优跟踪控制作为现代控制理论的一个重要分支，通过在给定约束条件下最小化指定的代价函数来实现对系统轨迹的跟踪。代价函数通常包括跟踪误差和控制输入，控制策略的生成不仅要保证跟踪误差最小化，还要兼顾控制输入的合理性，避免过度的资源消耗，在控制领域具有重要意义。

2、求解最优跟踪控制问题的方法主要有变分法和动态规划法，然而，由于实际中的电机系统非线性强、精确模型难以准确获得，这两种方法的求解往往极其困难。

技术实现思路

1、本技术旨在至少在一定程度上解决相关技术中的技术问题之一。

2、为此，本技术的第一个目的在于提出一种非线性电机伺服系统的最优轨迹跟踪控制方法，不依赖于系统的精确模型，能够处理任意非线性系统状态受不等式约束的最优跟踪控制问题。

3、本技术的第二个目的在于提出一种非线性电机伺服系统的最优轨迹跟踪控制装置。

4、为达上述目的，本技术第一方面实施例提出了一种非线性电机伺服系统的最优轨迹跟踪控制方法，包括：

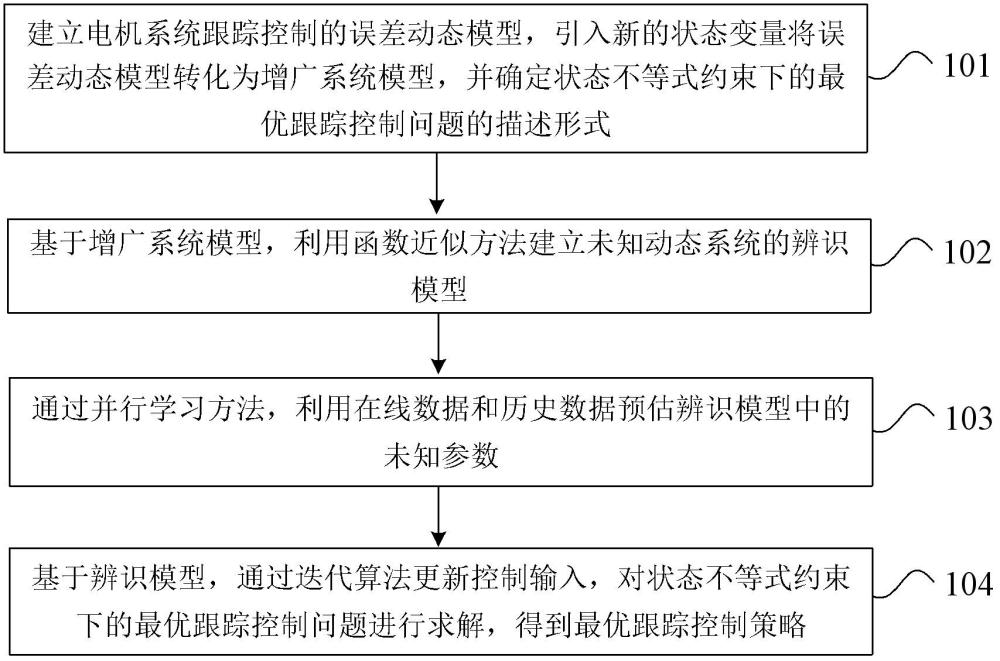
5、建立电机系统跟踪控制的误差动态模型，引入新的状态变量将误差动态模型转化为增广系统模型，并确定状态不等式约束下的最优跟踪控制问题的描述形式；

6、基于增广系统模型，利用函数近似方法建立未知动态系统的辨识模型；

7、通过并行学习方法，利用在线数据和历史数据预估辨识模型中的未知参数；

8、基于辨识模型，通过迭代算法更新控制输入，对状态不等式约束下的最优跟踪控制问题进行求解，得到最优跟踪控制策略。

9、本技术实施例的非线性电机伺服系统的最优轨迹跟踪控制方法，通过建立电机系统跟踪控制的误差动态模型，并引入新的状态变量将时变误差系统转化为非时变增广系统，进一步得到状态不等式约束下的最优跟踪控制问题的描述形式；基于增广系统模型，利用函数近似方法强大的非线性映射能力来建立未知动态系统的参数辨识模型；通过并行学习方法，同时利用在线数据和已有的历史数据来估计辨识模型中的未知参数；基于辨识模型，通过迭代算法来更新控制输入，得到不等式约束下的最优跟踪控制策略。本技术不依赖电机系统精确模型，实现了在保证电机系统状态满足已有的约束的同时，最小化有限时域内的跟踪误差和控制能耗，符合工程实际需求；本技术所考虑系统为非线性系统，具有现实意义。

10、可选地，在本技术的一个实施例中，建立电机系统跟踪控制的误差动态模型，包括：

11、定义电机非线性系统为：

12、

13、其中，是系统状态，为系统初始时刻，为系统初始状态，是系统控制输入，为u输入系统后的系统状态，为系统的动态函数，

14、定义电机非线性系统状态约束为：

15、

16、其中，为维列向量函数，代表存在个不等式约束；

17、定义系统跟踪信号为，跟踪误差为，对于最优跟踪控制问题，采用二次型性能指标表示代价函数，代价函数表示为：

18、

19、其中，代表一段预先确定的时间间隔，，为实对称正定矩阵，

20、误差动态模型的动态函数以及不等式约束表示为：

21、

22、引入新的状态变量将误差动态模型转化为增广系统模型，包括：

23、假设跟踪信号由未知动态函数生成，未知动态函数表示为：

24、

25、定义新的状态变量，增广系统表示为：

26、

27、新的状态变量所满足的不等式约束为：

28、

29、代价函数表示为：

30、

31、其中，矩阵定义为：

32、

33、确定状态不等式约束下的最优跟踪控制问题的描述形式，包括：

34、对于不等式约束，构造kelley-bryson罚函数作为代价函数，并将最优跟踪控制问题的求解转化无约束问题的求解，构造的代价函数表示为：

35、

36、其中，为一个单调递增的序列，且满足，罚函数中项为阶跃函数，公式化为：

37、

38、当增广系统状态满足所给定的不等式约束时，，无约束问题的解满足的条件为：

39、

40、最优性条件的简化形式为：

41、

42、其中，为协态量，为哈密顿函数，，。

43、可选地，在本技术的一个实施例中，基于增广系统模型，利用函数近似方法建立未知动态系统的辨识模型，包括：

44、令代表增广系统未知动态函数的第项，利用函数近似方法将其近似为：

45、

46、其中，为权重系数，为隐藏层个神经元的激活函数，为对应的近似误差；

47、定义权重系数的估计值为，令矩阵，，令激活函数向量为，未知动态系统的参数辨识模型表示为：。

48、可选地，在本技术的一个实施例中，通过并行学习方法，利用在线数据和历史数据预估辨识模型中的未知参数，包括：

49、采集在任意时刻下增广系统的历史数据点，历史数据点为，历史数据点包括增广系统的状态、控制输入以及状态的导数，定义矩阵，所采集的历史数据集合满足；

50、利用历史数据集合以及在线数据更新辨识模型中的未知参数，更新时的自适应更新律表示为：

51、

52、其中，和分别代表第次迭代过程中增广系统状态值和系数矩阵的估计值，、为学习率，和分别是第次迭代过程中增广系统状态和系数矩阵的估计误差。

53、可选地，在本技术的一个实施例中，最优跟踪控制策略的生成过程包括：

54、步骤s1：初始化系数、、，设定精度误差、、，选取初始控制输入以及初始系数矩阵估计值，测量在初始控制输入下的原系统状态，计算对应的增广系统的轨线以及代价函数，令，，其中，；

55、步骤s2：通过求解第一方程组更新控制输入，其中，第一方程组表示为：

56、

57、其中，，代表系数矩阵的前n列；

58、步骤s3：通过求解第二方程组更新系数矩阵，其中，第二方程组表示为：

59、

60、步骤s4：通过更新后的控制输入计算增广系统的轨线以及对应的代价函数；

61、步骤s5：重复进行步骤s2-s4，在每次重复后，令，，、为迭代步长，直至，

62、步骤s6：重复进行步骤s2-s5，在每次重复后，令，，，直至控制输入以及辨识模型收敛于给定的精度误差，其中，控制输入收敛于给定的精度误差，表示为：，辨识模型收敛于给定的精度误差，表示为：；

63、步骤s7：重复步骤s2-s6，在每次重复后，令，，，，，为迭代步长，直至增广系统的状态在给定的精度误差下满足不等式约束，得到辨识模型参数以及最优跟踪控制策略，其中，增广系统的状态在给定的精度误差下满足不等式约束，表示为：。

64、为达上述目的，本技术第二方面实施例提出了一种非线性电机伺服系统的最优轨迹跟踪控制装置，包括：

65、系统建立模块，用于建立电机系统跟踪控制的误差动态模型，引入新的状态变量将误差动态模型转化为增广系统模型，并确定状态不等式约束下的最优跟踪控制问题的描述形式；

66、系统建立模块，还用于基于增广系统模型，利用函数近似方法建立未知动态系统的辨识模型；

67、系统辨识模块，用于通过并行学习方法，利用在线数据和历史数据预估辨识模型中的未知参数；

68、计算求解模块，用于基于辨识模型，通过迭代算法更新控制输入，对状态不等式约束下的最优跟踪控制问题进行求解，得到最优跟踪控制策略。

69、本技术附加的方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本技术的实践了解到。