一种高超音速火箭车的温度和速度间歇控制方法

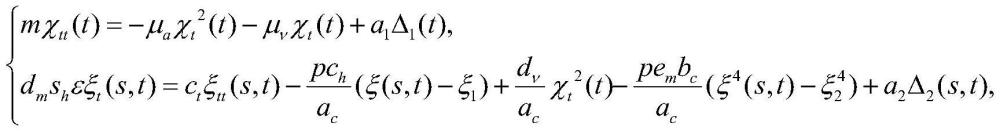
本发明涉及高超音速火箭车，具体为一种高超音速火箭车的温度和速度间歇控制方法。

背景技术：

1、高超音速火箭车可以在极短时间内到达目标区域，这种快速反应能力在国防安全方面具有重要的战略意义。因此在先进飞行技术、国防安全需求以及航天工程发展方向上，高超音速火箭车被广泛研究。由于高超音速火箭车在高超音速运行时，外部会产生极端的空气摩擦热，导致材料快速升温，并且此时空气流动具有强烈的非线性特性，比如湍流、激波等现象，可能影响系统的稳定性。此时，为了保证系统的稳定，对系统施加控制是必要的。

2、高超音速火箭车的控制系统在构造时存在以下难点：

3、(1)现有技术提出用由一组常微分方程和偏微分方程组成的系统对高超音速火箭车系统进行建模，并提出了一系列对于高超音速火箭车的温度和速度的控制策略，可在一定程度上实现对高超音速火箭车的温度和速度的控制，但这种方式无疑增加了计算的复杂性。

4、(2)在实际工程中，由于系统通信带宽等因素的限制，系统在连续控制的过程中，可能出现系统信息丢失、延迟等情况，使得系统控制精度的下降，稳定性受损。

5、(3)由于高超音速火箭车系统的复杂外部环境和部分非线性特性，因此难以保证控制系统的稳定性。

技术实现思路

1、本发明的目的在于提出一种高超音速火箭车的温度和速度间歇控制方法，解决了高超音速火箭车在状态信息不能完全测量和通信带宽有限情况下的控制问题，可以在有效地降低系统的通信负担的同时，保证系统的控制性能。

2、本发明采用的技术方案是：一种高超音速火箭车的温度和速度间歇控制方法，包括以下步骤：

3、s1、建立包含高超音速火箭车速度子系统和温度子系统的动力学模型；

4、引入误差变量，将所述动力学模型转化为高超音速火箭车的误差系统模型；

5、基于t-s模糊模型，将所述误差系统模型中存在的非线性部分进行线性化处理，进而产生模糊误差系统模型；

6、通过构造耦合状态变量，建立速度和温度的耦合模糊误差系统模型；

7、s2、基于高超音速火箭车的耦合模糊误差系统模型，设计用于估计所述高超音速火箭车系统状态的不连续状态观测器以及用于周期性控制所述高超音速火箭车的间歇反馈控制信号；

8、对高超音速火箭车的耦合模糊误差系统模型进行稳定性分析，根据稳定性确定所述间歇反馈控制信号的设计参数；

9、s3、使用代入设计参数后的间歇反馈控制信号对高超音速火箭车的速度和温度进行间歇控制。

10、作为优选方案，所述高超音速火箭车的动力学模型为：

11、

12、其边界条件表示为：

13、ξs(0,t)＝ξs(γ,t)＝0

14、其中，χ(t)表示高超音速火箭车在t时刻的位移，χt(t)和χtt(t)分别表示χ(t)关于时间的一阶导数和关于时间二阶导数；ξ(s,t)表示高超音速火箭车在时间t时，空间位置s处的温度，ξt(s,t)和ξtt(s,t)分别表示ξ(s,t)关于时间的一阶导数和关于时间二阶导数；s∈[0,γ]表示空间位置；ξs(0,t)和ξs(γ,t)分别表示ξ(s,t)在空间位置0处关于空间的一阶导数和在空间位置γ处关于空间的一阶导数；a1和a2是控制器系数，δ1(t)和δ2(s,t)分别表示高超音速火箭车ode速度子系统在时间t时的控制输入和高超音速火箭车pde温度子系统在时间t时空间位置s处的控制输入；m表示高超音速火箭车的质量；μa表示空气阻力系数；μv表示粘滞摩擦力系数；dm表示材料密度；sh表示材料的比热容；ε表示奇异摄动参数，并且0＜ε＜＜1；ct表示导热性；p表示周长；ch表示对流换热系数；ac表示横截面积；dv表示动态粘度；em表示材料的发射率；bc表示玻尔兹曼常数；ξ1表示表面周围介质的温度；ξ2表示表面法线方向远处的温度。

15、作为优选方案，高超音速火箭车的误差系统模型为：

16、

17、其边界条件表示为：

18、ξs(0,t)＝ξs(γ,t)＝0

19、系统输出表示为：

20、y1(t)＝c1x(t)

21、y2(s,t)＝c2ξ(s,t)

22、其中，x(t)表示高超音速火箭车在时间t时的速度误差，并且χz表示高超音速火箭飞行器在行驶过程中的稳态速度，且满足u1(t)＝δ1(t)-u1z；是一个待设计的正常数，u1z表示速度的稳态控制输入；xt(t)表示x(t)关于时间的一阶导数；g1(x(t))和g3(x(t))表示关于误差x(t)的非线性函数；b1、b2、c1和c2是常数；ξ(s,t)表示高超音速火箭车在时间t时和空间位置s处的温度误差，并且ξz表示高超音速火箭飞行器在行驶过程中的稳态温度；是一个待设计的正常数；

23、稳态温度ξz满足u2z表示温度的稳态控制输入；u2(t)＝δ2(t)-u2z；ξt(s,t)和ξss(s,t)表示ξ(s,t)关于时间的一阶导数和关于空间的二阶导数；g2(ξ(s,t))表示关于ξ(s,t)的非线性函数；r表示高超音速火箭车的偏微分方程子系统的反应扩散系数，并且r＞0；ξ(0,t)和ξ(γ,t)分别表示高超音速火箭车在时间为t时，空间位置为0处的温度误差和在时间为t时和空间位置为γ处的温度误差；ξs(0,t)和ξs(γ,t)分别表示ξ(s,t)在空间位置0处关于空间的一阶导数和在空间位置γ处关于空间的一阶导数；y1(t)和y2(s,t)代表高超音速火箭车系统的输出。

24、作为优选方案，高超音速火箭车的模糊误差系统模型为：

25、

26、其中：hi和分别表示ode速度子系统的隶属度函数和pde温度子系统的隶属度函数；ai，bi和cl是实数，i＝1,2,...,n，l＝1,2,...,n。

27、作为优选方案，高超音速火箭车的耦合模糊误差系统模型为：

28、

29、其中，和表示关于时间的一阶导数和关于空间的二阶导数；z-1(ε)表示矩阵z(ε)的逆矩阵。

30、作为优选方案，高超音速火箭车的不连续状态观测器为：

31、

32、其中，表示的估计值，和分别表示x(t)和ξ(s,t)的估计值，和表示关于时间的一阶导数和关于空间的二阶导数；表示的估计误差；表示x(t)的估计误差，表示ξ(s,t)的估计误差；k为自然数；ω表示间歇观测的周期；σ表示系统在一个周期内的控制时间；lo和lp为待设计的观测器增益，c3和c4为正常数。

33、作为优选方案，所设计的高超音速火箭车的间歇反馈控制信号为：

34、

35、u1(t)＝u2(s,t)＝0,t∈(kω+σ,(k+1)ω]

36、其中为k1和k2为待设计的控制器增益。所设计的控制信号为间歇状态反馈控制信号。由于系统的状态变量往往不能从系统外部直接测量得到，因此本方法通过不连续状态观测器来估计系统的状态，然后通过状态反馈控制来有效地改善系统的性能。

37、作为优选方案，建立李雅普诺夫函数，根据李雅普诺夫函数关于时间的导数对高超音速火箭车进行稳定性分析，确定系统在稳定性状态下观测器增益和控制器增益的设计参数，以及最小控制时间比率。

38、作为优选方案，所建立的李雅普诺夫函数v(t)为：

39、

40、其中，ds表示微分算子；

41、与现有技术相比，本发明的有益效果是：

42、1.本发明通过构造耦合向量将系统的状态耦合在一起，并将原系统重写为一个耦合系统，大幅降低了控制器设计过程的计算复杂度；

43、2.与连续控制策略相比，本发明结合了间歇控制方案，可以在控制高超音速火箭车的温度和速度的同时，降低系统的通信压力。

44、3.并且本发明考虑到系统的状态信息不能完全测量的情况，为系统设计了不连续的状态观测器，然后基于不连续的状态观测器对系统施加间歇控制。利用本发明方法，可以实现对过程对象的控制，具有很好的鲁棒性和稳定性，可以有效提高经济效益。