快速获取金属旋转对称体电磁散射特性的矩阵抽取方法与流程

本发明涉及电磁应用技术领域，特别涉及一种快速获取金属旋转对称体电磁散射特性的矩阵抽取方法。

背景技术：
金属旋转对称体是指能由母线绕固定轴旋转一周得到的物体。作为一类重要的雷达目标，如导弹体，天线罩等，人们已经对其电磁散射特性进行了相当多的研究。特别是在跟踪和识别空间目标上，旋转体的电磁散射仿真占据重要地位。利用旋转对称矩量法仿真和研究各类旋转体的电磁散射问题一直是电磁散射研究中重要的课题。Andreasen,M.G在1965年首先提出了旋转对称矩量法。文中将入射平面波利用傅立叶级数展开为相互正交的柱面波形式，利用各模式间的正交性，分别求解单一模式下的感应电流，然后进行线性叠加，从而求得散射场的分布(M.Andreasen,"Scatteringfrombodiesofrevolution,"AntennasandPropagation,IEEETransactionson,vol.13,pp.303-310,1965.)。但对建立的积分方程的求解采用的是点配法，计算简单但精度不高。J.R.MautzandR.F.Harrington利用等效电流的概念和电场边界条件建立了金属金属旋转对称体散射的电场积分方程(J.RMautzandR.F.Harrington,Generalizednetworkparametersforbodiesofrevolution,TechnicalReport,TR-687.SyracuseUniversity.Syracuse.NY13244.June1968)，将等效电流展开为关于φ的傅立叶（Fourier）级数和关于t的分段三角函数，然后利用数值方法中的矩量法（MoM）求解，解决了旋转金属体的散射问题。但当金属体形成谐振腔后，这种方法就失效了。J.R.Mautz.andR.F.Harrington又利用等效电流和等效磁流的概念和边界条件建立了金属散射体的混合场积分方程(J.R.MautzandR.F.Harrington,H-field,E-fieldandcombined-fieldsolutionsforconductingbodiesofrevolution,AEU321978,157-164)，解决了金属形成谐振腔后不能准确求解的问题。不论金属体是否形成了谐振腔，都能得到准确解。SDGedney,和RMittra使用快速傅里叶方法来加速金属旋转对称体矩量法计算（S.D.GedneyandR.Mittra,"TheuseoftheFFTfortheefficientsolutionoftheproblemofelectromagneticscatteringbyabodyofrevolution,"AntennasandPropagation,IEEETransactionson,vol.38,pp.313-322,1990.）。FFT方法加速了模式矩阵的形成，但却要一次存储所有模式矩阵，内存消耗很大。金属旋转对称体矩量法中的格林函数是以电流呈正弦分布的圆环为单位源产生的场，称为模式林函数。斜入射时需要的模式数随着入射波的倾斜角和计算对象在柱坐标系下最大截面半径的电尺寸的增大而增大，模式格林函数也随之剧烈振荡。使用闭式模式格林函数加速金属旋转对称体的计算是一种常用的克服积分振荡的方法。但该方法在仿真电大尺寸的金属旋转对称体时会出现发散（Y.WenMing,etal.,"ClosedFormModalGreen'sFunctionsforAcceleratedComputationofBodiesofRevolution,"AntennasandPropagation,IEEETransactionson,vol.56,pp.3452-3461,2008.）。现有仿真金属旋转对称体的方法存在以下问题：（1）FTT方法加速金属旋转对称体计算但对内存的消耗大，仿真的金属旋转对称体的规模有限，只对部分结构十分有效；（2）推导闭式模式格林函数来加速金属旋转对称体计算，操作繁琐，限制条件多；（3）对于快速计算电大尺寸旋转对称目标斜入射时的散射场，高次模式矩阵填充效率低。

技术实现要素：
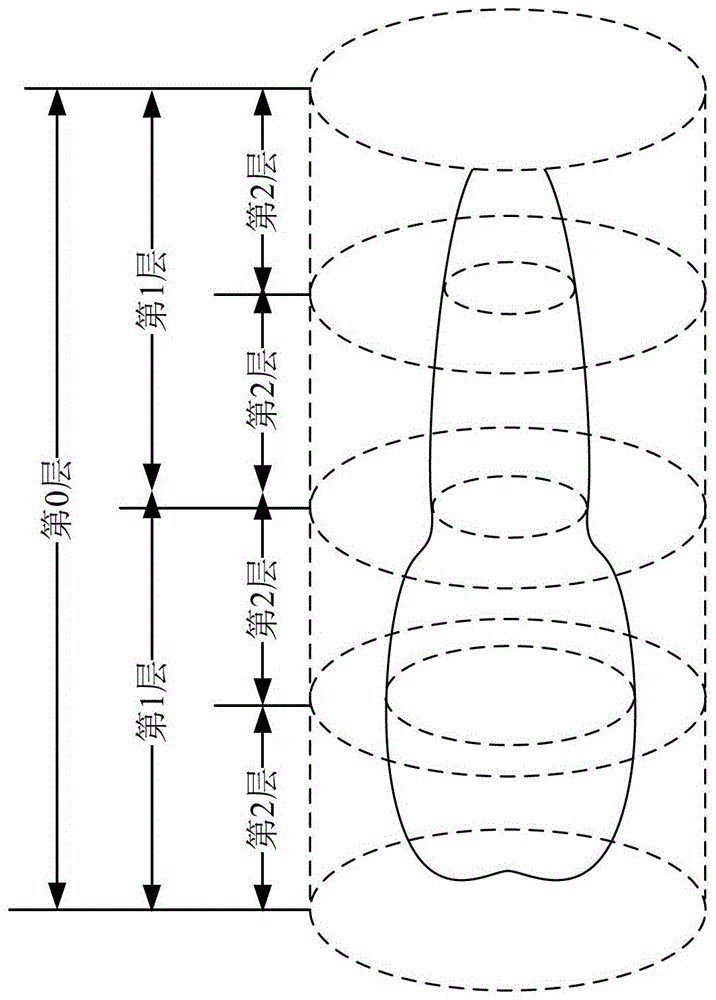
针对现有技术中存在的以上问题，本发明的目的在于提供一种快速稳定的仿真电大尺寸金属旋转对称体目标电磁散射特性的方法，该方法基于矩阵抽取方法，内存消耗低，矩阵填充和方程求解快。实现本发明目的的技术方案为：一种快速获取金属旋转对称体电磁散射特性的矩阵抽取方法，其包括步骤如下：第一步，建立金属旋转对称体的母线，按十分之一介质波长离散，形成了母线的剖分线段；第二步，采用二叉树结构对剖分线段进行分组，确定近场、远场组；第三步，使用具有傅里叶级数形式的旋转对称基函数展开未知散射电流；第四步，对金属旋转对称体边界建立混合场积分方程，使用矩量法离散混合场积分方程，得到模式阻抗矩阵方程；按照近、远场组将模式阻抗矩阵分成近场模式阻抗矩阵和远场模式阻抗矩阵；第五步，采用矩量法直接计算近场组第α个模式矩阵；使用矩阵抽取方法填充远场组第α个模式阻抗矩阵；计算第α个模式对应激励向量；使用迭代方法求解第α个模式矩阵方程，得到第α个模式散射电流系数；上述求解过程从第0个模式数开始，直到α＝Mod；第六步，将第五步得到的各个模式电流系数累加得到金属旋转对称体表面的电流，由互易定理计算得到雷达散射截面积。本发明与现有技术相比，其显著优点：（1）避免了一次存储所有模式阻抗矩阵，降低了内存消耗低；（2）由于仅需要计算一小部分远场互作用的矩阵元素，因而即使不使用闭式格林函数也可以高效的生成阻抗矩阵，而高次模的低秩性更明显，十分适合使用本发明方法计算；（3）由于远场矩阵的低秩特性，迭代求解是矩阵矢量乘的速度加快，整个求解时间大大缩减；（4）方法有坚实的数学基础，鲁棒性好，易于编程实现，可以在个人计算机上仿真近千个波长的电大金属旋转对称体的电磁散射特性。附图说明图1是本发明具体实施例的金属旋转对称体目标示意图。图2是本发明具体实施例的与待求金属旋转对称体共轴并能将其完全包围的圆柱结构示意图。图3是本发明具体实施例的二叉树近场组和远场组示意图。图4是本发明具体实施例的快速仿真金属旋转对称体电磁散射特性的方法流程图。图5是采用本发明具体实施例的快速获取金属旋转对称体电磁散射特性的矩阵抽取方法对金属圆柱进行仿真示意图。图6是本发明具体实施例的计算时间随未知量增加的复杂度曲线图。图7是本发明具体实施例的内存消耗随未知量增加的复杂度曲线图。具体实施方式为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图对本发明的具体实施方式做详细的说明，使本发明的上述及其它目的、特征和优势将更加清晰。本发明一种快速获取金属旋转对称体电磁散射特性的矩阵抽取方法，包括步骤如下：第一步，建立金属旋转对称体的母线，按十分之一介质波长离散，形成了母线的剖分线段；第二步，采用二叉树结构对剖分线段进行分组，确定近场、远场组；第三步，使用具有傅里叶级数形式的旋转对称基函数展开未知散射电流；第四步，对金属旋转对称体边界建立混合场积分方程，使用矩量法离散混合场积分方程，得到模式阻抗矩阵方程；按照近、远场组将模式阻抗矩阵分成近场模式阻抗矩阵和远场模式阻抗矩阵；第五步，采用矩量法直接计算近场组第α个模式矩阵；使用矩阵抽取方法填充远场组第α个模式阻抗矩阵；计算第α个模式对应激励向量（说明书中相应位置加以说明）；使用迭代方法求解第α个模式矩阵方程，得到第α个模式散射电流系数；上述求解过程从第0个模式数开始，直到α＝Mod；第六步，将第五步得到的各个模式电流系数累加得到金属旋转对称体表面的电流，由互易定理计算得到雷达散射截面积。图1是本发明具体实施例的金属旋转对称体目标示意图。图2是本发明具体实施例的与待求金属旋转对称体共轴并能将其完全包围的圆柱结构示意图。图3是本发明具体实施例的二叉树近场组和远场组示意图。图4是本发明具体实施例的快速仿真金属旋转对称体电磁散射特性的方法流程图。结合图1至图4，本发明是针对电大金属旋转对称体的仿真平台，它基于旋转对称矩量法和矩阵抽取方法，以达到对待求解散射体快速仿真的目的。具体步骤如下：第一步：建立金属旋转对称体的母线，按十分之一介质波长离散，形成了母线的剖分线段；首先使用Ansys等商用软件建立金属旋转对称体的母线，并按照λ/10对母线进行离散，其中λ表示波长，εr表示相对介电常数。金属旋转对称体表面的等效电磁流将展开成周向方向向的傅立叶（Fourier）级数和母线方向的分段三角函数。通过这一步我们得到立体模型的一维剖分基本参数：剖分的线段数，线段长度，线段编号，线段端点的编号和坐标。第二步：采用二叉树结构对剖分线段进行分组，确定近场、远场组；用一个虚拟圆柱将金属旋转对称体包围住，如图2所示，该圆柱体为第零层组节点，对该圆柱体二等分，形成的每个子圆柱体为第一层组节点，然后再对每个子圆柱体二等分，直到圆柱高为1到2个波长之间，最后形成的子圆柱体为最细层组节点，每个组节点即为一组；同一层相邻的组为近场组，不相邻的组为远场组，再在此分组的基础上建立二叉树，子层的远场组为父层的近场组。第三步：使用具有傅里叶级数形式的旋转对称基函数展开未知散射电流；在金属旋转对称体表面建立局部坐标系，是表面法向单位矢量，是沿方位角方向的单位矢量，是沿母线方向的单位矢量，满足n表示基函数编号，m表示测试函数编号；利用旋转对称体结构特性，将表面r'点散射电磁流J(r')表示为：分别表示第α个模式数对应的方向和方向第n个基函数，由以下公式给出，分别是对应的基函数展开系数，N为总基函数个数；其中Tn(t)为第n个三角基函数，有公式给出；t为剖分线段上的一点在母线方向的取值，ρ(t)是剖分线段上t处对应的半径值。其中和表示第n条剖分线段的起点和终点，和表示第n+1条剖分线段的起点和终点，t为剖分线段上的一点在母线方向的取值；根据旋转对称体的最大半径Rmax、入射频率f和入射俯仰角θinc确定总模式数Mod：Modmax＝kρRmax+1(4)其中μ为空气磁导率，ε为空气介电常数。若入射角度垂直于旋转轴，则总模式数为1；第四步：对金属旋转对称体边界建立混合场积分方程，使用矩量法离散混合场积分方程，得到模式阻抗矩阵；按照近、远场的索引关系将模式阻抗矩阵分成近场模式阻抗矩阵和远场模式阻抗矩阵；建立积分方程：（1）电场积分方程EFIE（2）磁场积分方程MFIE其中k为入射波波数，J(r)表示场点r的散射电流，J(r')表示源点r'的散射电流，Einc(r)表示场点r的入射电场，Hinc(r)表示场点r的入射磁场，ω表示入射波角频率。若目标为开放结构，使用电场积分方程（16）计算；若目标为闭合结构使用混合场积分方程计算，所谓混合场积分方程CFIE为电场积分方程EFIE和磁场积分方程MFIE的线性叠加：CFIE＝γEFIE+(1-γ)ηMFIE(7)其中γ为混合参数，0≤γ≤1，η表示空气中的波阻抗。使用公式（13）基函数和其共轭作为测试函数，应用矩量法基本原理对积分方程进行离散，得到一些列模式阻抗矩阵方程：ZαIα=Vα(8)其中Zα为模式α对应的模式阻抗矩阵，Iα为模式α对应的电流系数，Vα为模式α对应的激励向量。模式阻抗矩阵包含四个子模块：其中各个子模块的矩阵元素由下面公式给出：其中pq表示t,φ，即代表选择基函数或测试函数的上标t,φ中任两种组合。对应于模式阻抗矩阵中的四个不同的子模块；根据近、远场组关系可将（20）式分解为：Zα＝Zαnear+Zαfar(11)其中Zαnear表示近场模式阻抗矩阵，Zαfar表示远场模式阻抗矩阵；第五步，采用矩量法直接计算近场组第α个模式矩阵；使用矩阵抽取方法填充远场组第α个模式阻抗矩阵；计算第α个模式对应激励向量；使用迭代方法求解第α个模式矩阵方程，得到第α个模式散射电流系数；上述求解过程从第0个模式数开始，直到α＝Mod；5.1采用矩量法直接计算近场组第α个模式矩阵；Zαnear近场模式阻抗矩阵使用传统的旋转对称体矩量法公式（22）逐个元素填充，并按照稀疏格式存储；5.2使用矩阵抽取方法填充远场组第α个模式阻抗矩阵；远场组之间的作用Zαfar采用矩阵抽取方法填充。而Zαfar又包含四个小矩阵Zαttfar,Zαtφfar,Zαφtfar和Zαφφfar，先对Zαttfar使用矩阵抽取方法填充。用矩阵代表矩量法中两个远场组的相互作用阻抗矩阵Zαttfar。矩阵抽取方法通过两个满秩矩阵的乘积形式来构造近似矩阵用来近似估计即其中r为矩阵的有效秩，为场组中包含的未知量的个数，为源组中包含的未知量的个数，和为两个满秩矩阵。因此，矩阵抽取近似方法只需要保存和这两个较小的矩阵即可，这样存储量就由降到计算复杂度由原来的O(N2)，经过新的矩阵矢量乘可以降低到2rN，其中N为未知量个数。设C=[C1,…,Cr]和L=[L1,…,Lr]为包含从矩阵中挑选出的行和列的索引的数组，pk为矩阵P的第k列，qk为矩阵Q的第k行，其中代表矩阵的第C1行，为矩阵在第k次循环得到的近似矩阵；所述矩阵抽取方法如下：初始化循环初始值：初始化第一个行索引C1=1，令X=0。初始化近似误差矩阵的第一行：在第一行中寻找最大值从而确定第一个列索引L1：得到Q矩阵的第一行：初始化近似误差矩阵的第一列：得到P矩阵的第一列：在第一列中寻找最大值从而确定第二个行索引C2：第k次循环：更新近似误差矩阵的第Ik行：在第Ck行中找到最大值从而确定第k个列索引Lk：得到Q矩阵的第ｋ行：更新近似误差矩阵的第Lk列：得到P矩阵的第ｋ列：判断收敛误差：如果迭代结束，否则找下一个行索引Ik+1：进入第k+1次循环，直至停止条件满足。通过上述操作得到矩阵P和矩阵Q，从而得到了矩阵的近似矩阵，完成了一个子远场模式矩阵的计算。重复上述行列矩阵抽取方法的过程，完成所有远场子模式矩阵Zαttfar的填充。其它三个矩阵Zαtφfar,Zαφtfar,Zαφφfar按照Zαttfar得到的行列信息[C1,…,Cr]和[L1,…,Lr]进行抽取。重复上述矩阵抽取方法逐层计算各个远场组之间互作用远场模式阻抗矩阵，完成第α个模式的填充过程。5.3计算第α个模式对应激励向量Vα；设入射场为均匀平面波，设置入射角度为（θinc，φinc）及极化方式（垂直极化或水平极化）。入射电场矢量Einc表达式为：Einc＝E0e-jkr，E0表示电场方向矢量，入射磁场矢量Hinc的表达式为：其中η为空气的波阻抗，表示传播方向。则激励向量Vα为：其中激励向量中对应的元素为：其中，ρ表示r点距z轴的垂直距离；5.4使用迭代方法求解第α个模式矩阵方程，得到第α个模式散射电流系数Iα；GMRes为一种常用的迭代方法，这里被用来求解模式阻抗矩阵（20）；重复上述5.1-5.4，逐个求解所有模式阻抗矩阵方程，得到各个模式电流系数；随着模式数的增高模式矩阵特性值整体变小，矩阵抽取行列时需要降低截断精度，否则计算效率下降，一般在模式数大于10以后可以取0.1以上。第六步，将第五步得到的各个模式电流系数使用公式（12）累加得到金属旋转对称体表面的电流，由互易定理计算得到雷达散射截面积σ。由互易定理可以推导得到每平方米的雷达散射截面积的θθ,θφ,φθ,φφ四种可能的情况下对应的公式：其中λ表示波长，(θsca,φsca)为远区场方向，上标分别代表θ或φ，表示散射场的极化方向，表示入射场的极化方向，代表或表示方向极波（θ或φ方向）俯仰角θsca时入射波α模式方向分量激励向量，表示α=0，表示方向极化波入射时对应的第α模式方向分量散射电流系数。实施例：图5是采用本发明具体实施例的快速获取金属旋转对称体电磁散射特性的矩阵抽取方法对金属圆柱进行仿真示意图，根据本发明所述方法对一个半径为1m高为100m的金属圆柱进行了仿真，入射场设置为均匀平面波，频率为0.3GHz，入射角度为（0°，0°），平行极化波，模式数为1。其结果与原始的旋转对称方法吻合很好，证明了该方法的正确性。图6是本发明具体实施例的计算时间随未知量增加的复杂度曲线图。图7是本发明具体实施例的内存消耗随未知量增加的复杂度曲线图，两者皆达到了O(N)，充分显示了其高效性。