一种基于改进型粒子群算法的道路三维线形自动优化方法与流程

本发明涉及公路或铁路的选线领域，特别是一种基于改进型粒子群算法的道路三维线形自动优化方法。

背景技术：
依据铁(公)路的基本的走向及主要技术标准，自动选线目的在于同时实现铁路或公路的平面和纵断面的自动设计。自动选线过程中需要从满足约束条件的多个线路方案中找到一条最优的方案(通常是经济费用最省)。由于其目标函数要通过数字高程模型内插才能获得，并且包含了各种费用，通常该函数是不可微的。由于起点终点之间满足约束条件的线路方案有无穷多个，在优化的过程中，需要考虑项目建设中众多复杂的因素，而各因素间相互作用、互相制约，因此，自动选线是一个十分复杂的问题。现有技术中对该问题的优化通常是对于线路的平面和纵断面的选线分别进行优化，容易陷入局部最优解，得到的选线结果只能作为局部优化且这种模型的计算效率不高。随着地理信息系统(GIS)技术的发展，应用GIS技术进行道路自动选线。然而现有的道路路选线设计方法由于不能够直接对地理信息进行识别、分析和利用，选线结果不尽人意，难以实现实际应用。GIS现有的地理信息快速的获取方法、科学的表达模式以及强大的空间检索分析能力为自动选线投入实用提供了技术支持。如文献[1]：MinWookKang,PaulSchonfeld,NingYang.PrescreeningandRepairinginaGeneticAlgorithmforHighwayAlignmentOptimization[J].Computer-AidedCivilandInfrastructureEngineering.24(2009)109–119。然而，现有技术中并未提供一种利用GIS同时进行线路的平面和纵断面的选线优化。

技术实现要素：
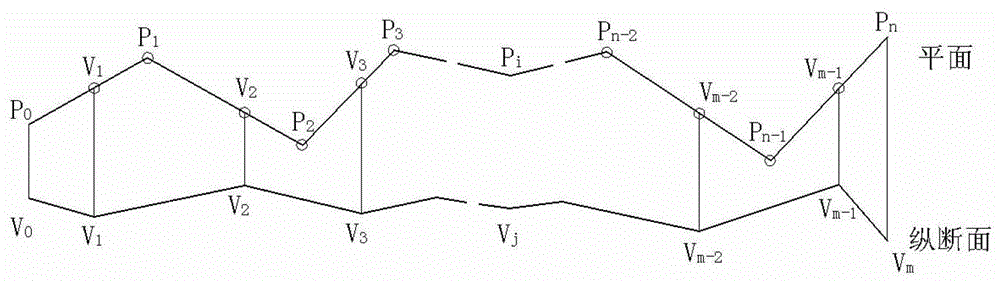
本发明提供了一种基于改进型粒子群算法的道路三维线形自动优化方法，其目的在于，克服现有技术的不足，同时优化线路的平面和纵断面的选线，避免在优化过程中出现的局部最优问题。一种基于改进型粒子群算法的道路三维线形自动优化方法，首先建立道路三维线形优化目标函数，依据设定线路平面及纵断面的约束条件、道路建设单价、线路取点间隔及线形优化目标区域，采用改进型粒子群算法对利用ArcGIS软件获得导向线方案的三维线形的平面交点及纵断面变坡点参数同时进行优化，获得自动优化后的道路三维线形；所述三维线形的平面交点及纵断面变坡点参数是指平面交点的平面坐标(x,y)、半径R及缓长l，纵断面变坡点里程mil及高程z；三维线形上所有平面交点及纵断面变坡点参数作为改进型粒子群算法中的粒子k；所述改进型粒子群算法模型为：其中，vkdt为粒子k第d维在第t次迭代的速度分量；ω为权重系数设定值；xkdt为粒子k第d维当前的位置分量；t为迭代的次数；int为向下取整函数，原型为int(number)，取小于或等于number的最大的整数；ceil为向上取整函数，原型为ceil(number)，取大于或者等于number的最小整数；为整数区间内均匀分布的随机数，当时，当时，为整数区间内均匀分布的随机数，当时，当时，c1为控制粒子在飞向自身最好位置方向的步长；c2为控制粒子在飞向全局最好位置方向的步长；rand1、rand2是两个介于[0，1]范围的随机数；pbestkdt表示粒子k在第t次迭代之前的历史最好位置；gbestkdt表示种群在第t次迭代之前的全局历史最好位置；c1取2.0，c2取2.0。所述的基于改进型粒子群算法的道路三维线形自动优化方法，具体包括以下步骤：步骤1：建立道路三维线形目标函数F：式中，i为横断面序号；b为桥梁的序号；t为隧道的序号；j为土地类型序号；IK为线形设计区间中横断面的个数；TK为线形设计区间中隧道座数；BK为设计区间中桥梁座数；YK为用地类型总个数；C为土石方工程单价；Cb为第b座桥梁的施工单价；Ct为第t座隧道的施工单价；Cj为第j种类型土地的用地单价；Si为第i个设计横断面的面积；Δw为两相邻横断面间的距离；Lb为第b座桥梁的长度；Lt为第t座隧道的长度；Aj为第j种土地类型的用地面积；沿三维线形平面的法向量方向对线路进行剖分获得线路的横断面；步骤2：设定三维线形平面及纵断面的约束条件、道路建设单价、三维线形平面取点间隔及三维线形优化目标区域xmin≤x≤xmax,ymin≤y≤ymax；(1)平面约束条件(a)最小曲线半径约束，平面交点Pi平曲线半径为r1i，不小于设定的最小曲线半径rmin，rmin≤r1i(i＝1,2,...,n-1)；(b)最短圆曲线长度约束，两相邻缓和曲线间的圆曲线长度不小于设定的最短圆曲线长度式中：为圆曲线长度；αi为圆曲线夹角；(c)最短夹直线约束，平面夹直线最小长度为平面夹直线长度Li,i+1-Ti-Ti+1必须大于设定的平面夹直线最小长度为式中：Li,i+1为平面交点i至交点i+l间的距离；Ti为平面交点i处的切线长；Ti+1为平面交点i+1处的切线长；(2)纵断面约束条件(a)坡长约束，纵断面设计坡长须满足最小坡长的限制；两相邻竖曲线的切线长之和小于该坡段长度，即：其中，lcj-1,lcj分别为纵断面变坡点j-1及j的里程；分别为纵断面变坡点j-1及j处的切线长；(b)坡度约束，纵断面第j段的设计坡度ij应该满足规范规定的允许坡度，即：式中：hj,hj-1分别为纵断面变坡点j与j-1的设计高程；为纵断面坡段j的坡段长；imin,imax分别为规定的最小、最大坡度；(c)相邻坡段坡度差约束，相邻坡段的坡度差的绝对值不超过允许的最大值Δimax，即(d)控制点高程约束线路在指定点处的设计高程hj应当满足最大最小高程(hmax,hmin)要求，即：hmin≤hj≤hmax(3)线形优化目标区域设定为xmin≤x≤xmax,ymin≤y≤ymax，同时满足以下条件：1)禁止通过设定区域，即禁区；设置禁区的地价费用或地面高程为无穷大，即从目标区域中排除禁区；2)必须通过设定区域；设平面必经区域中心点为O，计算O点距离线路中心线的距离do，设定较小值ε，并满足do≤ε，则线路可以从该区域通过，即该区域中必须包含有所选线路；步骤3：从三维线形优化目标区域中，采用改进型粒子群算法寻找最优线形，适应度函数为F；步骤a)采用由ArcGIS软件获得导向线方案的三维线形作为初始线形，初始线形上所有平面交点及纵断面变坡点参数作为粒子，设置粒子群种群大小、迭代次数及初始种群，利用改进型粒子群算法搜索更新初始线形上的所有交点的位置，输出最好解x1，即粒子位置构成的最佳三维线形；步骤b)若步骤a)中搜索得到的三维线形中包含非三维线形优化目标区域中的位置，则采用静态搜索更新步骤a)得到的最好解x1在三维线形优化目标区域中的速度，利用速度更新最好解x1，获得第二最好解x2；步骤c)以步骤b)获得的第二最好解x2作为初始探测点进行轴搜索，获得第三最好解x3；步骤d)将步骤c)获得的第三最好解x3输入ArcGIS软件，自动获得道路最优线形。所述步骤3中步骤b)的静态搜索的搜索过程如下：对于落入不可行区域的粒子，速度更新方程中，设定惯性权重系数ω＝0，使得粒子新的速度与原飞行无关，只取决于粒子的当前位置、历史最好位置和粒子群的历史最好位置，即速度更新方程为：vkdt+1＝c1·rand1·(pbestkdt-xkdt)+c2·rand2·(gbestkdt-xkdt)(16)其中：vkdt为粒子k第d维在第t次迭代的速度分量；ω为权重系数设定值；xkdt为粒子k第d维当前的位置分量；t为迭代的次数；c1控制粒子在飞向自身最好位置方向的步长；c2控制粒子在飞向全局最好位置方向的步长；rand1、rand2是两个介于[0，1]范围的随机数；pbestkdt表示粒子k在第t次迭代之前的历史最好位置；gbestkdt表示种群在第t次迭代之前的全局历史最好位置；c1取2.0，c2取2.0。所述步骤3中步骤c)的轴搜索的搜索过程如下：以第二最好解x2作为第一轮探测即初始探测点为x0，依次沿d维坐标轴的方向进行以下探测过程搜索得到多个探测点，从多个探测点中选择使得目标函数值F最小的点作为轴搜索得到的最好点；设放大因子α>1，缩减因子β∈(-1，0)，沿各轴方向的步长为δ1，δ2，...，δd；每轮探测的起点和终点分别为y(1)和ye(即yn+1)，令y(1)＝x(k)，x(k)为第k次转轴后的搜索起点，d(i)表示d维坐标轴中第i个坐标轴的方向，按如下规则进行探测；y(i+1)＝y(i)+δid(i)从以x(k)为基点沿各个方向探测所得的点y(j)对应的目标函数值F中，选择一个目标函数值最小的对应点作为好解将好解与x(k)点对应的目标函数值F比较进行比较，按照下式更新步长：判断是否满足以下任一条件，若满足，即完成探测，获得当前得到的好解并将作为第三最好解x3，否则进入下一轮探测：(1)沿各轴方向不能找到比初始探测点x0的目标函数值更小的点y(j)；(2)各个方向的步长δj均达到设定的最小值ε，ε的取值范围是0.01-0.1。有益效果本发明提供了一种基于改进型粒子群算法的道路三维线形自动优化方法，通过对同一目标区域进行铁路和公路自动选线优化测试结果分析可知：应用本发明提出的理论和方法能快速高效地同时进行线路的平面和纵断面的选线优化，优化后的三维线形能很好的绕避障碍物和适应地形，可以作为工程设计人员提供前期设计参考，降低设计人员劳动强度。①方案多样性好、效率高。最终生成并非单一方案，而是一个包含绕避方案和架设桥隧方案等不同特点的最优方案群。利用Rosenbrock方法与PSO算法，保证了优化后的线路方案的多样性，为线路设计人员提供更多有参考价值的比选方案，避免了由于设计人员主观因素而遗漏可行方案。②全局最优化搜索方法，避免陷入局部最优。改进的PSO算法从理论上保证了线形优化在三维搜索空间中的全局最优，更容易搜索到全局最优方案。③适用于大范围选线。ArcGIS地理信息系统拥有强大的空间分析能力和海量数据处理能力，能方便快捷地处理大范围的地形地貌，为大范围选线提供强有力的支撑体系。改进的PSO算法能依据线路必经地区将大范围选线问题分成多个相互关联的段落，分别进行线路搜索，并在程序设计时利用多线程等技术同时搜索，提高搜索效率。附图说明图1为RPSO整数算法流程图；图2为纵断面上的变坡点在平面上的投影示意图；图3为本发明的应用示意图；图4为本发明的线路寻优过程示意图；图5为实例的地理环境信息示意图；图6为自动选线参数设置示意图；图7为线形优化方案群示意图；图8参数对比分析图。具体实施方式下面结合附图和实施例对本发明做进一步说明：本发明一种基于改进型粒子群算法的道路三维线形自动优化方法，首先建立道路三维线形优化目标函数，依据设定线路平面及纵断面的约束条件、道路建设单价、线路取点间隔及线形优化目标区域，采用改进型粒子群算法对利用ArcGIS软件获得导向线方案的三维线形的平面交点及纵断面变坡点参数同时进行优化，获得自动优化后的道路三维线形；所述三维线形的平面交点及纵断面变坡点参数是指平面交点的平面坐标(x,y)、半径R及缓长l，纵断面变坡点里程mil及高程z；三维线形上所有平面交点及纵断面变坡点参数作为改进型粒子群算法中的粒子K；所述改进型粒子群算法模型为：其中，vkdt为粒子k第d维在第t次迭代的速度分量；ω为权重系数设定值；xkdt为粒子k第d维当前的位置分量；t为迭代的次数；int为向下取整函数，原型为int(number)，取小于或等于number的最大的整数；ceil为向上取整函数，原型为ceil(number)，取大于或者等于number的最小整数；为整数区间内均匀分布的随机数：当时，当时，为整数区间内均匀分布的随机数：当时，当时，c1为控制粒子在飞向自身最好位置方向的步长；c2为控制粒子在飞向全局最好位置方向的步长；rand1、rand2是两个介于[0，1]范围的随机数；pbestkdt表示粒子k在第t次迭代之前的历史最好位置；gbestkdt表示种群在第t次迭代之前的全局历史最好位置；c1取2.0，c2取2.0。改进型粒子群算法流程图如图1所示；本实例的原始数据是内蒙古自治区乌兰察布市某地区5公里区段内的地形以及房屋、河流、道路、用地等地物信息资料。资料收集中部分数据可直接应用既有的AutoCAD图形文件及数据，并基于ArcGIS9.3软件环境完成资料的收集和处理。地形及地物的相关属性信息则依据实地收集资料输入系统，建立了选线区域的信息数据库——数字高程模型、房屋、河流、道路以及用地等信息数据，从而得到了区域内智能选线的原始资料，如图5所示，图中所示系统基于ArcGIS9.3软件环境开发及应用。本次选线是在选线区域内应用本发明设计一条长度约5km的三级公路。由图5可看出本选线区域为山岭重丘区，地形丘陵起伏、沟壑纵横，无不良地质状况。根据具体情况设置参数：设计时速为60km/h；最小曲线半径为200m；曲线间最小直线长度为360m；平曲线最小长度300m；最大纵坡差为10％；土石方单价为20元/m3；桥梁单价为30000元/m2；隧道单价为25000元/m2，具体参数见图6。如图3和图4所示为本实例应用本发明的示意图。步骤1：建立道路三维线形目标函数F：式中，i为横断面序号；b为桥梁的序号；t为隧道的序号；j为土地类型序号；IK为线形设计区间中横断面的个数；TK为线形设计区间中隧道座数；BK为线形设计区间中桥梁座数；YK为用地类型总个数；C为土石方工程单价；Cb为第b座桥梁的施工单价；Ct为第t座隧道的施工单价；Cj为第j种类型土地的用地单价；Si为第i个设计横断面的面积；Δw为两相邻横断面间的距离；Lb为第b座桥梁的长度；Lt为第t座隧道的长度；Aj为第j种土地类型的用地面积；沿三维线形平面的法向量方向对线路进行剖分获得线路的横断面；步骤2：设定三维线形平面及纵断面的约束条件、道路建设单价、三维线形平面取点间隔及三维线形优化目标区域xmin≤x≤xmax,ymin≤y≤ymax；(1)平面约束条件(a)最小曲线半径约束，平面交点Pi平曲线半径为r1i，不小于设定的最小曲线半径rmin，rmin≤r1i(i＝1,2,...,n-1)；(b)最短圆曲线长度约束，两相邻缓和曲线间的圆曲线长度不小于设定的最短圆曲线长度式中：为圆曲线长度；αi为圆曲线夹角；(c)最短夹直线约束，平面夹直线最小长度为平面夹直线长度Li,i+1-Ti-Ti+1必须大于设定的平面夹直线最小长度为式中：Li,i+1为平面交点i至交点i+l间的距离；Ti为平面交点i处的切线长；Ti+1为平面交点i+1处的切线长；(2)纵断面约束条件(a)坡长约束，纵断面设计坡长须满足最小坡长的限制；两相邻竖曲线的切线长之和小于该坡段长度，即：其中，lcj-1,lcj分别为纵断面变坡点j-1及j的里程；分别为纵断面变坡点j-1及j处的切线长；(b)坡度约束，纵断面第j段的设计坡度ij应该满足规范规定的允许坡度，即：式中：hj,hj-1分别为纵断面变坡点j与j-1的设计高程；为纵断面坡段j的坡段长；imin,imax分别为规定的最小、最大坡度；(c)相邻坡段坡度差约束，相邻坡段的坡度差的绝对值不超过允许的最大值Δimax，即(d)控制点高程约束线路在指定点处的设计高程hj应当满足最大最小高程(hmax,hmin)要求，即：hmin≤hj≤hmax(3)线形优化目标区域设定为xmin≤x≤xmax,ymin≤y≤ymax，同时满足以下条件：1)禁止通过设定区域，即禁区；设置禁区的地价费用或地面高程为无穷大，即从目标区域中排除禁区；2)必须通过设定区域；设平面必经区域中心点为O，计算O点距离线路中心线的距离do，设定较小值ε，并满足do≤ε，则线路可以从该区域通过，即该区域中必须包含有所选线路；步骤3：从三维线形优化目标区域中，采用改进型粒子群算法寻找最优线形，适应度函数为F；步骤a)采用由ArcGIS软件获得导向线方案的三维线形作为初始线形，初始线形上所有平面交点及纵断面变坡点参数作为粒子，设置粒子群种群大小、迭代次数及初始种群，利用改进型粒子群算法搜索更新初始线形上的所有交点的位置，输出最好解x1，即粒子位置构成的最佳三维线形；步骤b)若步骤a)中搜索得到的三维线形中包含非三维线形优化目标区域中的位置，则采用静态搜索更新步骤a)得到的最好解x1在三维线形优化目标区域中的速度，利用速度更新最好解x1，获得第二最好解x2；步骤c)以步骤b)获得的第二最好解x2作为初始探测点进行轴搜索，获得第三最好解x3；步骤d)将步骤c)获得的第三最好解x3，输入ArcGIS软件，自动获得道路最优线形。所述步骤3中步骤b)的静态搜索的搜索过程如下：对于落入不可行区域的粒子，速度更新方程中，设定惯性权重系数ω＝0，使得粒子新的速度与原飞行无关，只取决于粒子的当前位置、历史最好位置和粒子群的历史最好位置，即速度更新方程为：vkdt+1＝c1·rand1·(pbestkdt-xkdt)+c2·rand2·(gbestkdt-xkdt)其中：vkdt为粒子k第d维在第t次迭代的速度分量；ω为权重系数设定值；xkdt为粒子k第d维当前的位置分量；t为迭代的次数；c1控制粒子在飞向自身最好位置方向的步长；c2控制粒子在飞向全局最好位置方向的步长；rand1、rand2是两个介于[0，1]范围的随机数；pbestkdt表示粒子k在第t次迭代之前的历史最好位置；gbestkdt表示种群在第t次迭代之前的全局历史最好位置；c1取2.0，c2取2.0。所述步骤3中步骤c)的轴搜索的搜索过程如下：以第二最好解x2作为第一轮探测即初始探测点为x0，依次沿d维坐标轴的方向进行以下探测过程搜索得到多个探测点，从多个探测点中选择使得目标函数值F最小的点作为轴搜索得到的最好点；设放大因子α>1，缩减因子β∈(-1，0)，沿各轴方向的步长为δ1，δ2，...，δd；每轮探测的起点和终点分别为y(1)和ye(即yn+1)，令y(1)＝x(k)，x(k)为第k次转轴后的搜索起点，按如下规则进行探测；y(i+1)＝y(i)+δid(i)从以x(k)为基点沿各个方向探测所得的点y(j)对应的目标函数值F中，选择一个目标函数值最小的对应点作为好解将好解与x(k)点对应的目标函数值F比较进行比较，按照下式更新步长：判断是否满足以下任一条件，若满足，即完成探测，获得当前得到的好解并将作为第三最好解x3，否则进入下一轮探测：(1)沿各轴方向不能找到比初始探测点x0的目标函数值更小的点y(j)；(2)各个方向的步长δj均达到设定的最小值ε，ε的取值范围是0.01-0.1。图2为纵断面上的变坡点在平面上的投影示意图；选线基本参数设置完成后，可以通过点取或录入的方式设置设计线路的起终点。然后，通过现有选线系统，生成线路的导向线方案，如图7所示，其中展示了方案2、方案6、方案8和方案9的导向线走向。从导向线方案中选取方案8进行线形优化。对方案8进行线形优化，配置合理的线形参数，经过采用本发明提供的方法，生成的线路的三维线形优化方案，如图8所示。经三维线形优化后可以得到线路的平纵面数据信息。线路的平面交点数据如表2所示，纵断面变坡点数据如表3所示。表2平面交点数据表3纵断面变坡点数据为了对系统智能选线的运行效率进行测试，将本实例与文献[1]中的实例进行了对比分析，具体的运行结果数据对比见表4。表4运行效率对比图从上表可以看出，与文献[1]的实例规模相比，本实例的选线区域面积为其2倍，线路长度为其4倍。但本实例的运行时间比文献[1]缩短了近一倍，而且迭代次数较少，可以迅速收敛。所以与相对文献[1]比较，本文方法的运行效率较高。