一种双馈风电机组机电暂态模型的建模方法与流程

本发明属于电力系统模拟
技术领域：
，尤其是一种双馈风电机组机电暂态模型的建模方法。
背景技术：
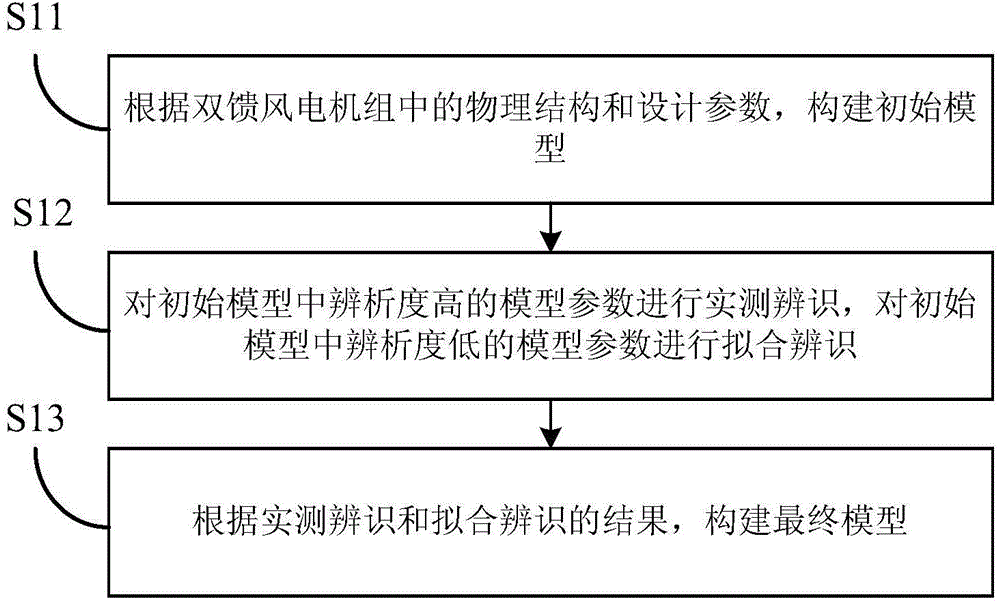
：随着能源资源紧缺、气候环境恶化问题日益突出，在除水电外可再生能源发电中风力发电因成本较低和技术最成熟而得到迅猛发展。海上风电场具有风速高、风力稳定、干扰少、发电量大等优势，已成为未来风电发展的重要选择。我国东部沿海地区海上风能资源丰富且距离负荷中心近，具备大规模发展的资源条件和市场需求，开发海上风电可有效改善东部电力供应结构能源供应情况。风电等可再生能源的大规模应用，必然带来集中接入、远距离传输以及风电场内部集电线路网络化等问题，从而改变电力系统的运行特征。对接入点而言，规模化的风电场对系统运行的影响需要一起关注，需要有效掌握电网运行状态变化与风电机组和风电场暂态特性的之间的关联关系和相互影响，以提前掌握大规模风电场接入系统后的系统安全稳定状态，确保系统的安全稳定运行。其中，实现风电机组的建模和大规模风电场的等值是其中最基础最核心的问题之一。技术实现要素：本发明的目的之一是提供一种双馈风电机组机电暂态模型的建模方法，以解决现有技术中根据厂商提供的设计参数建立模型，导致模型可靠性较低的问题。在一些说明性实施例中，所述双馈风电机组机电暂态模型的建模方法，包括：根据双馈风电机组中的物理结构和设计参数，构建初始模型；对所述初始模型中辨析度高的模型参数进行实测辨识，对所述初始模型中辨析度低的模型参数进行拟合辨识；根据所述实测辨识和拟合辨识的结果，构建最终模型。与现有技术相比，本发明的说明性实施例包括以下优点：本发明解决了双馈风电机组缺乏与实际相符的计算模型参数问题，通过实测辨识和拟合辨识，可以得到当前系统的精确度高的模型参数，利用得到的模型参数再构建系统模型，系统模型可靠性高，为电网的安全稳定运行提供有力支撑。附图说明此处所说明的附图用来提供对本发明的进一步理解，构成本申请的一部分，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。在附图中：图1是按照本发明的说明性实施例的流程图；图2是按照本发明的说明性实施例的流程图；图3是按照本发明的说明性实施例的控制模型；图4是按照本发明的说明性实施例的控制模型；图5是按照本发明的说明性实施例的控制模型；图6是按照本发明的说明性实施例的控制模型；图7是按照本发明的说明性实施例的控制模型；图8是按照本发明的说明性实施例的控制模型；图9是按照本发明的说明性实施例的控制模型。具体实施方式在以下详细描述中，提出大量特定细节，以便于提供对本发明的透彻理解。但是，本领域的技术人员会理解，即使没有这些特定细节也可实施本发明。在其它情况下，没有详细描述众所周知的方法、过程、组件和电路，以免影响对本发明的理解。如图1所示，公开了一种双馈风电机组机电暂态模型的建模方法，包括：S11、根据双馈风电机组中的物理结构和设计参数，构建初始模型；S12、对所述初始模型中辨析度高的模型参数进行实测辨识，对所述初始模型中辨析度低的模型参数进行拟合辨识；S13、根据所述实测辨识和拟合辨识的结果，构建最终模型。本发明解决了双馈风电机组缺乏与实际相符的计算模型参数问题，通过实测辨识和拟合辨识，可以得到当前系统的精确度高的模型参数，利用得到的模型参数再构建系统模型，系统模型可靠性高，为电网的安全稳定运行提供有力支撑。在一些说明性实施例中，所述根据双馈风电机组中的物理结构和设计参数，构建初始模型，具体包括：根据所述双馈风电机组中的变流器控制系统、双馈电机和桨距角控制系统的物理结构和设计参数，构建所述初始模型。在一些说明性实施例中，所述对所述初始模型中辨析度高的模型参数进行实测辨识，具体包括:对所述初始模型中辨析度高的模型参数进行静态试验实测和动态试验实测。在一些说明性实施例中，对所述初始模型中辨析度高的模型参数进行静态试验实测，具体包括：对所述初始模型中的以下环节进行静态试验实测：电压外环控制PID、功率测量、锁相环、有功控制PID、无功控制PID和低电压穿越控制限制。在一些说明性实施例中，对所述初始模型中辨析度高的模型参数进行动态试验实测，具体包括：对所述初始模型中的定子电阻和定子电抗进行动态试验实测。在一些说明性实施例中，所述对所述初始模型中辨析度高的模型参数进行动态试验实测，还包括：对桨距角控制系统中的PID参数，低电压穿越控制目标值，动作时间进行动态试验实测。在一些说明性实施例中，所述对所述初始模型中辨析度低的模型参数进行拟合辨识，具体包括：对逆变器控制系统的电流内环控制PID等环节进行拟合辨识。在一些说明性实施例中，所述对逆变器控制系统的电流内环控制PID进行拟合辨识，具体包括：采用最小二乘法或遗传算法，对逆变器控制系统的电流内环控制PID等环节进行拟合辨识。在一些说明性实施例中，在所述根据所述实测辨识和拟合辨识的结果，构建最终模型之后，还包括：校验所述最终模型，结果满足预先设定的误差标准，确定所述最终模型；否则，返回对所述初始模型中辨析度高的模型参数进行实测辨识，对所述初始模型中辨析度低的模型参数进行拟合辨识，重新构建所述最终模型。在一些说明性实施例中，所述校验所述最终模型的过程，包括：进行故障情况及负载情况的组合工况下的低电压穿越特性试验，每个所述组合工况下的试验结果满足预先设定的误差标准；确定所述最终模型的结果满足预先设定的误差标准。如图2所示，公开了一种双馈风电机组机电暂态模型的建模方法，包括：S21、输入双馈风电机组中的变流器控制系统、双馈电机和桨距角控制系统的物理结构和设计参数，形成双馈风电机组初始模型；S22、根据双馈风电机组初始模型，分析其模型参数的可辨识性，对可辨性高的参数进行实测辨识，对可辨性低的参数进行拟合辨识；其中，步骤S22中，具体包括：对辨析度高的环节进行动态试验实测和静态试验实测，包括：1)、静态试验实测：对变流器控制系统的模型参数中的电压外环控制PID、功率测量、锁相环、有功控制PID、无功控制PID、低电压穿越控制限制等环节进行静态试验实测；根据静态实测数据对电压外环控制PID、功率测量、锁相环、有功控制PID、无功控制PID、低电压穿越控制限制等参数进行辨识；2)、动态试验实测：①对双馈电机的模型参数中的定子电阻、定子电抗等环节进行动态试验实测；根据实测数据对定子电阻、定子电抗等参数进行辨识；②对桨距角控制系统的模型参数中的PID参数，低电压穿越控制目标值，动作时间等环节进行动态试验实测；根据动态实测数据对桨距角控制系统的PID参数，低电压穿越控制目标值，动作时间等参数进行辨识；对辨析度低的环节进行动拟合辨识，包括：1)、对逆变器控制系统的模型参数中的电流内环控制PID等环节进行拟合辨识；拟合辨识可以采用最小二乘法进行计算，也可以采用遗传算法进行计算。S23、根据辨识结果，构建双馈风电机组模型；其中，对双馈风电机组模型的进行低电压穿越特性实测，测试数据作为判断建模精度是否合格的依据；在所述步骤(10)中，考虑到双馈风电机组模型的特殊性，需要进行与国标要求一致的20个工况下的低电压穿越特性试验，以获取风机的全面特性，全面校核模型参数精度。20个工况即故障情况与负载情况的组合工况。S24、建立双馈风电机组模型仿真算例，进行仿真计算；S25、计算结果是否满足误差标准；满足进入步骤S26，否则，返回步骤S22；S26、确定最终模型，并汇总模型参数辨识结果，并且保存相关计算校核中间过程。上述说明性实施例中，所述初始模型具体为：双馈电机的物理结构如图3所示的控制模型；其中，us为…定子电压，is为定子电流，Rs为定子电阻，χs为……定子感抗，χr为……转子感抗，为定子磁链，为转子磁链，Rr为……转子电阻，ir为……转子电流，ur为转子电压，χm为互感。对应的数学方程如下：vqs=ψds-Rsiqsvds=-ψqs-Rsidsvqr=-dψqrdt+sψdr-Rriqrvdr=-dψdrdt-sψqr-Rridr]]>ψqs=(xm+xs)iqs+xmiqrψds=(xm+xs)ids+xmidrψqr=(xm+xr)iqr+xmiqsψdr=(xm+xr)idr+xmids]]>其中的v、ψ、i分别表示电压、磁链和电流，下标d和q分别代表d轴和q轴分量，下标s和r分别代表定子和转子变量。另外，桨距角控制系统是根据功率、转速等信号控制风电机组的桨距角，正常情况下实现跟踪最大功率的目的，在故障条件下，实现控制发电机转速的目的，如图4所示的控制模型，其中的ωgen为机组转速，Pgen为机组有功功率，Tr为转速测量时间常数，Tpr为功率测量时间常数，Kp为转速控制比例时间常数，Kpp为功率控制比例时间常数，KI为转速控制积分时间常数，KPI为功率控制积分时间常数，Tp为限制环节时间常数，ωref为转速参考量，Pref为功率参考量，β为桨桨距角给定量。该模型中发电机转速和电磁功率作为输入信号，经过PI环节，给出桨距角控制信号，模型后半部分包括桨距角幅值和变化速率的最大最小限制以及一阶惯性环节，一阶惯性环节模拟具体执行时的伺服特性。模型实际应用中，可选择输入信号发电机转速和/或电磁功率。有功功率控制方式考虑两种控制方式：●转速作为控制信号的控制方式；●恒定转矩控制方式。第一种控制方式主要根据发电机转速控制电磁转矩，进而实现控制电磁功率,具体模型如图5所示，其中，Kptrq为比例时间常数，Kitrq为积分时间常数，Tpc为限制环节时间常数，Pmin为功率下限，Pmax为功率上限。第二种恒定转矩控制方式如6所示，其中，Tref为转矩参考量。发电机无功功率控制一般采用如下几种模式：●缺省控制模式●恒定功率因数控制；●根据机端电压控制。其中，缺省控制模式下，无功功率参考值设置为0。恒定功率因数控制和机端电压控制对应的模型如图7所示，其中，Vreg为机组电压，Vref为机组电压参考量，KPV为比例时间常数，KVI为积分时间常数，TV为惯性环节时间常数，Qmin为无功下限，Qmax为无功上限，Qref为无功参考量，TPE为……有功测量时间常数，PFref为机组容量参考量。机侧变频器可以采用保留功率控制回路、电流控制回路的详细控制模型，但考虑到机电暂态程序中对于时间尺度较小环节存在数值稳定性问题，同时详细控制模型对机电暂态仿真结果影响有限，可以考虑采用简化模型，即转子电压控制，如图8所示：其中，Us为机组定子电压，Idmin为d轴转子电流下限，Idmax为d轴转子电流上限，Idref为d轴转子电流参考量，Iqre为q轴转子电流参考量，Iq为q轴转子电流，Id为d轴转子电流，Vdmax为d轴转子电压上限，Vqmin为q轴转子下限，Vdr为d轴转子电压输出量，Vqr为……q轴转子电压输出量，KQP为无功环比例时间常数，KQI为无功环积分时间常数。该模型中有功、无功控制信号直接转换为电流信号经过PI环节控制转子电压。正常运行条件下，有功、无功电流限幅环节采用有功功率优先的方式，即无功限幅根据最大电流限制和有功电流计算得到：Iqmax=Imax2-Idref2]]>网侧变频器控制的目标是维持直流电压为设定值、保证变频器运行的功率因数为1(零无功)。这意味着网侧变频器与电网只交换有功功率，无功交换只通过定子回路完成。可以将其简化，这样只考虑直流电压控制环节，具体模型如图9所示：其中，UDC为变流器直流侧电压，UDC,ref为直流侧电压参考量，KPUDC为控制环节比例时间常数，KIUDC为控制环节积分时间常数，Id.grid,ref为网侧电流输出参考量。上述中的初始模型通过本发明的说明性实施例中的静态检测和动态检测确定其具体值，将获得的值放入对应的模型中，即获得所述最终模型。以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本发明的限制。当前第1页1 2 3