一种实现自然对数和自然指数函数的可重构阵列结构的制作方法

本发明涉及使用可编程可重构的阵列结构实现自然对数和自然指数函数的迭代计算。

背景技术：

近年来，可重构计算技术逐渐成为高性能计算机系统研究中的一个新的热点，它的出现让过去传统意义上的硬件和软件界限变得模糊。可重构计算使硬件变得可“编译”，可以在一个结构上完成各种各样的任务，大幅度提高系统的总体性能。

在一些应用场合会先后用到自然对数（lnx）和自然指数（ex）函数的结果，传统的硬件实现一种结构只能完成一种函数的计算，而本发明中的可重构阵列结构可以在不改变结构的情况下，只通过改变编程、重新配置就可以依次实现两种函数的计算。

技术实现要素：
。

本发明实施的内容是提出一种使用8个处理元(PE)构成的可编程可重构的阵列结构，而且在该结构上既可以实现lnx函数的8次迭代计算，也可以实现e^x函数的8次迭代计算。

本发明实施的内容是提出一种使用8个处理元(PE)构成的可编程可重构的阵列结构，而且在该结构上既可以实现lnx函数的8次迭代计算，也可以实现e^x函数的8次迭代计算。

为实现上述目的，本发明所采用的技术方法如下：

在8个处理元（PE）的一号地址中存入事先计算好的ln(1+2^-i),i=0,1,2,3,4,5,6,7的值，分别为0.69314718、0.40546511、0.22314355、0.11779303、0.06062462、0.03077165、0.01550418、0.00778214；

在处理元（PE1）中进行第一次迭代运算，计算x⁽¹⁾=x⁽⁰⁾(1+2^-0)，并判断当时x⁽¹⁾<1，x⁽¹⁾保留迭代结果，y⁽¹⁾=y⁽⁰⁾-ln(1+2^-0)，否则x⁽¹⁾取迭代前的值，y⁽¹⁾=y⁽⁰⁾ ；具体实现过程是：

1）进行加法运算将初始值x⁽⁰⁾的值存入寄存器R1中；

2）进行加法运算将1存入寄存器R2中；

3）进行移位运算将R1左移R2位存入寄存器R3中；

4）进行加法运算将256存入寄存器R2中；

5）进行判断，如果R3<R2，进行加法运算，R3的值还是R3的值，再进行减法运算R0减去1号地址中的值存入R4中；如果R3>R2，进行加法运算，R3的值就是R1的值，再进行加法运算，R4的值为R0的值；跳转出判断运算；

6）进行加法运算，将R4的值存入寄存器R3中；

同理，在处理元（PE2,PE3,PE4,PE5,PE6,PE7,PE8）中进行剩下的相同原理的7次迭代，依次将二进制的指令全部存在指令存储器中；

在处理元（PE1）中进行第一次迭代运算；首先计算y⁽¹⁾=y⁽⁰⁾-ln(1+2^-0)，并判断当y⁽¹⁾≥1时，y⁽¹⁾保留迭代结果，x⁽¹⁾=x⁽⁰⁾ (1+2^-0)，否则y⁽¹⁾取迭代前的值，x⁽¹⁾=x⁽⁰⁾ ；具体实现过程为：

1）进行加法运算将初始值y⁽⁰⁾的值存入寄存器R1中；

2）进行加法运算将1存入寄存器R2中；

3）进行加法运算将256存入寄存器R6中；

4）进行减法运算将R1减去1号地址中的值存入R4中；

5）进行判断，如果R4<R0，进行加法运算将R1的值存入R4中，再进行加法运算将R6的值存入R5中；

6）如果R4>R0，进行加法运算，R4的值不变，再进行移位运算将R6左移R2位存入R5中；7）跳转出判断运算；

8）进行加法运算，依次将将R4和R5的值存入寄存器R3中；

同理，在处理元（PE2,PE3,PE4,PE5,PE6,PE7,PE8）中进行剩下的相同原理的7次迭代，将二进制指令全部存在指令存储器中；

完成两函数二进制指令的存储后，通过配置处理元（PE）来完成重构。

本发明提出了一种可重构的阵列结构，可以实现lnx和e^x函数的8次迭代计算，这样针对同一应用中先后需要这两种不同的超越函数的场合，具有较大优势，不仅节约了资源，而且缩短了等待时间，提高了运算效率。

附图说明

附图用来提供对本发明的进一步理解，并且构成说明书的一部分，用来解释本发明，并不构成对本发明的限制。在附图中：

图1为本发明的4×2的阵列结构图；

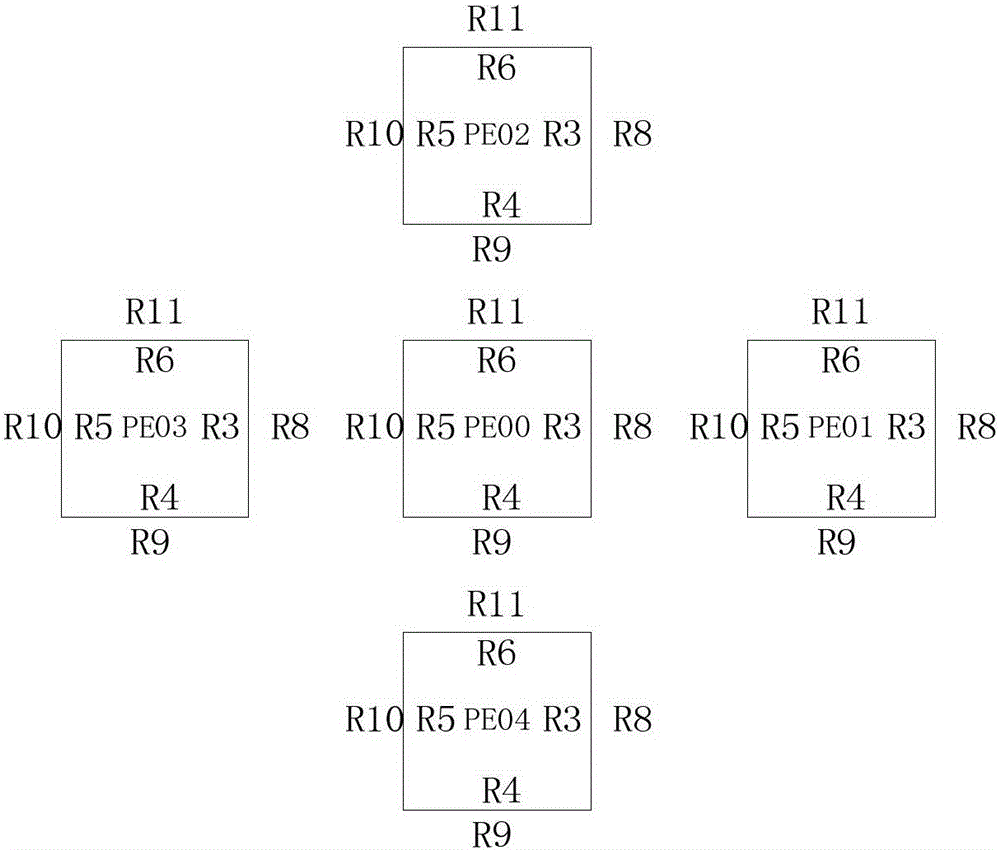
图2为本发明实施例提供的PE邻接互联示意图；

图3为在该结构实现的lnx和e^x函数的算法结构图。

具体实施方式

本发明实施提供了一种使用8个PE构成的可编程可重构的流水结构，如图1所示。每两个相邻的PE间采用邻接互连，如图2所示，当从左向右传数据时寄存器R3和寄存器R10相邻；当从上向下传数据时寄存器R4和寄存器R11相邻；当从右向左传数据时寄存器R5和寄存器R8相邻。当PE00需要传递数据给PE01时，只需要将数据写入到寄存器R3中，下一个时钟周期时寄存器R10接收来自R3的数据完成相邻处理器间的数据传递。

实现lnx函数的算法具体如下：

该算法属于回退分解算法（restoring decomposition algorithm），迭代公式为

（1）

每一次的迭代按d_i=1进行迭代，若x⁽ⁱ⁾(1+2^-i)<1，则d_i=1，否则d_i=0，迭代终止的条件为：x^(m)=1；

迭代终止时：y^(m)y⁽⁰⁾+lnx⁽⁰⁾ ，令y⁽⁰⁾=1，则y^(m) lnx⁽⁰⁾ 。

由于该算法的收敛速度与数据表示的精度密切相关。设操作位数为k位的精度，考虑到当ε²<1ulp(Unit of Last Place)时，ln(1+ε)＝ε-ε²/2+ε³/3-…≈ε，即当迭代次数i＞|k/2时，ln(1+d_i2^-i)≈d_i2^-i，当i＞k时，2^-i≈0，可停止迭代。考虑到，本结构中每个PE中的操作数采用8位整数、8位小数共16位有符号定点数表述，最高位为符号位，精度为8，因此使用8个PE迭代8次来实现lnx的计算。

具体实现步骤如下（图3）：

步骤一：在8个PE的1号地址中分别存入事先算好的ln(1+2^-i),i=0,1,2,3,4,5,6,7的数值，分别为0.69314718、0.40546511、0.22314355、0.11779303、0.06062462、0.03077165、0.01550418、0.00778214；

步骤二：在PE1中完成i=1时的第一次迭代：

1）寄存器R1中存入计算初值x⁽⁰⁾=x；

2）在寄存器R2中存入值1；

3）R1左移R2位结果放到寄存器R3中；

4）R2中放入数值256（定点数前8整数，后8位小数，所有256其实就是1）；

5）判断R2和R3的大小，如果R3<R2，跳转到第9条指令R3的值不变，R4等于0减去1号地址中存的值；否则继续，R3等于R1的值，R4等于0；

6）将R3邻接互连传到PE2；

7）等三拍后，将R4的值存入R3传给PE2；

步骤三：在PE2中完成i=2时的第二次迭代：

1）寄存器R1存入1；

2）寄存器R2中存入256；

3）中将数据传过来后将R10存入R5中；

4）R5右移R1位存入R3中；

5）R5加R3存入R3中；

6）判断R2和R3的大小，如果R3<R2，跳转到第16条指令R3的值不变，R4等于0减去1号地址中存的值；否则继续，R3等于R1的值，R4等于0；

7）将R3邻接互连传到PE3；

8）等三拍后，将R4的值存入R3传给PE3；

按照上面相同的方式，依次在PE3，PE4，PE5，PE6，PE7，PE8中完成剩下的迭代，在PE8中输出运算结果；

实现e^x函数的算法如下所示：

该算法也属于回退分解算法（restoring decomposition algorithm）迭代公式如下：

（2）

每一次的迭代按d_i=1进行迭代，若y⁽ⁱ⁾-ln(1+2^-i)≥0，则d_i=1，否则d_i=0，迭代终止的条件为：有y^(m)=0；

迭代终止时： ，令x⁽⁰⁾=1，则。

具体实现步骤如下（图3）：

步骤一：在8个PE的1号地址中分别存入事先算好的ln(1+2^-i),i=0,1,2,3,4,5,6,7的数值，分别为0.69314718、0.40546511、0.22314355、0.11779303、0.06062462、0.03077165、0.01550418、0.00778214；

步骤二：在PE1中完成i=1时的第一次迭代： 1）寄存器R1中存入计算初值x⁽⁰⁾=x；

2）在寄存器R2中存入值1；

3）R2中放入数值256（定点数前8整数，后8位小数，所有256其实就是1）；

4）R1减去1号存储中的值存入寄存器R4中；

5）判断R4和R0（默认为0）的大小，如果R4<R0，跳转到第9条指令R4的值等于R1的值，R5等于R0加上R6；否则继续，R4的值不变，R5等于R6左移R2位；

6）将R4邻接互连传到PE2；

7）等三拍后，将R5的值存入R3传给PE2；

步骤三：在PE2中完成i=2时的第二次迭代：

1）寄存器R1存入1；

2）寄存器R2中存入256；

3）将数据传过来后将R10存入R5中；

4）R1减去1号存储中的值存入寄存器R4中；

5）判断R4和R0（默认为0）的大小，如果R4<R0，跳转到第16条指令R4的值等于R1的值，R5等于R0加上R6；否则继续，R4的值不变，R5等于R6左移R2位；

6）将R4邻接互连传到PE2；

7）等三拍后，将R5的值存入R3传给PE3；

按照上面相同的方式，依次在PE3，PE4，PE5，PE6，PE7，PE8中完成剩下的迭代，在PE8中输出运算结果；

完成两函数二进制指令的存储后，通过配置处理元（PE）来完成重构。