一种基于新序列的十六进制运算方法与流程

本发明涉及计算机组成原理领域和逻辑代数领域，具体来说，涉及一种基于新序列的十六进制运算方法。

背景技术：

目前国际上通用的计算机主要使用二进制，俄罗斯研制过三进制计算机但没有大量生产。二进制是用0和1两个数码表示的数制，它的基数是2，进位规则为“逢二进一”借位规则为“借一当二”由德国人莱布尼茨发现，跟中国八卦中的阴阳理论有异曲同工之处。早期计算装置的研制主要采用十进制，现代计算机采用二进制与爱尔兰的乔治布尔的逻辑代数的研究有关，计算机由逻辑电路组成，逻辑电路通常有两种状态：开关的接通与断开，这两种状态正好可以用“1”和“0”表示。逻辑代数是逻辑运算的理论依据，二进制只有两个数码，正好与逻辑代数中的“真”和“假”相吻合。

日常生活中人们习惯使用十进制，数值输入计算机时使用十进制，送入机器后再转换成二进制数，运算完成后再将二进制转换成十进制供人们阅读。二进制表示一个数时，位数太多，加上阅读不方便，很多时候使用传统的十六进制来代替二进制，传统的十六进制数一位可以表示二进制数四位。科学家们在研究的光子计算机，量子计算机，生物计算机仍然在使用二进制，有一定的局限性，如果能有一种直接进行十六进制运算的计算机，那将突破这种局限。

涉及到的技术名称介绍：

十六进制：它由0-9，a-f组成，字母不区分大小写。与进制的对应关系是：0-9对应0-9，a-f对应10-15。它逢十六进一，与二进制之间的关系转换方便简单，使用很广泛。

逻辑代数运算规则：逻辑代数又称布尔代数，是研究逻辑关系的一种数学工具，被广泛用于数字电路的分析和设计。逻辑代数和普通代数一样可以用字母表示变量，但变量的取值只能是0和1，它表示两种逻辑状态，在研究实际问题时，0和1所代表的含义由具体的研究对象而定。所以逻辑代数所表达的是逻辑关系而不是数值关系，这是它与普通代数的本质区别。逻辑代数有三种基本逻辑运算——与运算(0·0＝0，0·1＝0，1·0＝0，1·1＝1)，或运算(0+0＝0，0+1＝1，1+0＝1，1+1＝1)，非运算(非0＝1，非1＝0)，其它各种逻辑运算由这三种基本运算组成。

技术实现要素：

本发明的目的是提供一种基于新序列的十六进制运算方法，能够为研制以十六进制为基础的计算机提供一种新的方法。

本发明的目的是通过以下技术方案来实现的：

一种基于新序列的十六进制运算方法，包括：

采用新序列，以00，01，10，11，0#，0i，1#，1i，#0，#1，i0，i1，##，#i，i#，ii十六个代码组成，每个代码以两个符号为一组，接下来再组合一组即：0100，0101，0110，0111，010#，010i，011#，011i，01#0，01#1，01i0，01i1，01##，01#i，01i#，01ii，(0100-01ii等同于传统十六进制数10，11，12，13，14，15，16，17，18，19，1a，1b，1c，1d，1e，1f)接下来是1000，1001，1010，1011，100#，100i，101#，101i，10#0，10#1，10i0，10i1，10##，10#i，10i#，10ii，1100，1101，1110，1111，110#，110i，111#，111i，11#0，11#1，11i0，11i1，11##，11#i，11i#，11ii，0#00，0#01，0#10，0#11，0#0#，0#0i，0#1#，0#1i，0##0，0##1，0#i0，0#i1，0###，0##i，0#i#，0#ii，0i00-0iii，1#00-1#ii，1i00-1iii，#000——iiii，再组合一组010000，010001，010010等等，一直排列下去，随着位数的增加表示数的范围也越大，新序列用两个符号组合等同于传统十六进制的一位，它组成一种机制，具有逢十六进一的特点，可以像传统十六进制一样具有连贯性即00+1＝01，01+1＝10， 10+1＝11，11+1＝0#，0#+1＝0i，0i+1＝1#，1#+1＝1i，1i+1＝#0，#0+1＝#1，#1+1＝i0，i0+1＝i1，i1+1＝##，##+1＝#i，#i+1＝i#，i#+1＝ii，ii+1＝0100……如此下去，当然0，1，#，i这四个符号也可以用0，1，x，y来代替。本发明采用0，1，#，i是有一定的含义的，它继承了传统二进制的原理，同时#与0形状相近，i与1形状相近，这使得新序列更便于记忆和理解；

采用一种运算规则，从最后一位开始往左数分别记为个位，十位，百位，千位，万位，十万位等，个位与十位是一组，百位与千位是一组，万位与十万位是一组等等，运算规则是：0+0＝0，0+1＝1，当1+1在个位上时1+1＝0进位是1进向十位，当1+1发生在十位上时1+1＝0进位是#进位迂回至个位重新与个位上的结果相加，1+#＝i，当1+i发生在个位上时，1+i＝#进位是1，当1+i发生在十位上时1+i＝#进位是#进向个位重新与个位上的结果相加，当#+#发生在个位上时#+#＝0进位#，当#+#发生在十位上时#+#＝0进位为1进向百位，当#+i发生在个位上时#+i＝1进位为#，当#+i发生在十位上时#+i＝1进位为1进向百位，当i+i发生在个位上时i+i＝0进位为i，当i+i发生在十位上时i+i＝0进位为1+#此时进位1进向百位，进位#进向个位重新与个位上的结果相加，将上述进位规则排列整齐如下：

要实现加法运算必须有一套与之相对应的新的基本的逻辑代数运算规则：

下面推导a+bc＝(a+b)(a+c)

现说明新序列下两个二位数相加：

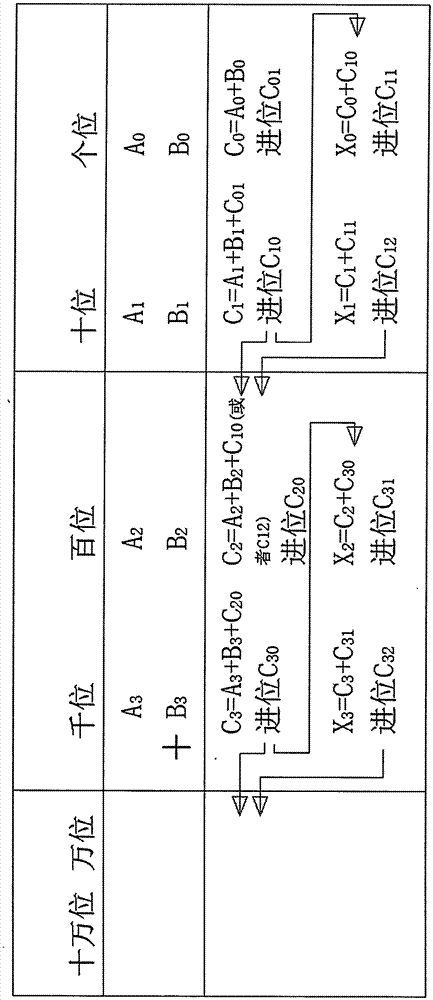
a1a0+b1b0的运算过程，个位上a0+b0＝c0进位记为c01，十位上a1+b1+c01＝c1进位记为c10根据运算规则c10可能进向个位或进向百位，也可能既进向个位也进向百位；

如果c10进向个位则c0+c10＝x0即为结果的个位，进位记为c11，c1+c11＝x1即为结果的十位，进位记为c12，这时c12的值是0或者1，它进向百位，a1a0+b1b0＝0c12x1x0；

如果c10进向百位时，c10为1，则a1a0+b1b0＝01c1c0；

如果c10既进向个位也进向百位即c10＝1+#，此时1进向百位，#进向个位，c0+#＝x0即为结果的个位，进位记为c11，c1+c11＝x1即为结果的十位，a1a0+b1b0＝01x1x0；

两个二位数相加的结果不会超过01i#，它是ii+ii的结果；

更多位数的新序列数相加就是重复两个二位数相加的过程，但是要考虑从低位来的进位。

本发明的有益效果为：本发明应用设计的新序列及所带的属性和新设计的基本的逻辑代数规则加上为新序列所设计的进位规则能完成一种基于新序列的十六进制的运算，在此基础上可以实现减法，乘法，除法的操作，可发展为一个用硬件实现直接进行十六进制各种运算的可行性系统。

附图说明

下面对实施例中需要使用的附图作简单的介绍，显而易见地，下面描述的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它附图；

图1两个二位数加法运算的流程图；

图2两个四位数加法运算的流程图；

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚，完整的描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例；基于本发明中的实施例，本领域普通技术人员所获得的其它实施例，都属于本发明保护的范围。

为使本发明的目的，技术方案更加清楚明白，以下参照附图并举实施例，对本发明作进一步详细说明。

实施例：

一种基于新序列的十六进制运算方法，本实施例采用1i+1i，#1+#i，i1+i1，iiii+i11i为例，包括以下步骤：

1i+1i，个位上i+i＝0进位i，十位上1+1+i＝i进位#进向个位，个位上结果为0+#＝#，进位0，十位上为i，所以1i+1i＝i#。

#1+#i，个位上1+i＝#进位为1，十位上#+#+1＝1，进位为1进向百位，#1+#i＝011#。

i1+i1，个位上1+1＝0进位1，十位上i+i+1＝1进位为1+#，1进向百位，#进向个位，再次个位上0+#＝#，十位上1+0＝1，i1+i1＝011#。

iiii+i11i，个位上i+i＝0进位为i，十位上i+1+i＝1进位为1+#，1进向百位，#进向个位，个位上的结果为0+#＝#，进位为0，十位上的结果为1+0＝1，百位千位上重复个位十位上的方法运用新序列进位规则，要考虑从十位来的进位1，百位上i+1+1＝i进位1，千位上i+i+1＝1进位为1+#，1进向万位，#进向百位，再次百位上i+#＝1进位为#，千位上1+#＝i，运算结束，iiii+i11i＝01i11#。

以上所述仅为本发明的几个实例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。