用于算术和函数合成的量子算法的制作方法

量子计算机承诺用于诸如因式分解、量子模拟和优化之类的大量重要问题的大幅加速。尽管量子特性已经被证明是这些算法的强大的资源，但是这些算法中许多的基础通常归纳为具有Hadamard门的经典可逆逻辑。这对于诸如量子线性系统算法之类的算法尤其如此，其承诺指数加速，但强烈地依赖于实现经典算术。对于实际的反演问题，可能需要数百个辅助(ancilla)量子位来实现可逆地执行算术所需的算术运算。通常，算术运算的量子实现使用可逆电路来通过使用由Kitaev在“Quantum computations：algorithms and error correction，”Russian Math.Surveys 52：1191-1249(1998)、以及Cleve等人在“Quantum algorithms revisited，”Proc.London Society of London(Series A)454：339-354(1997)中所描述的“相位反冲(phase-kickback)”方法来实现目标系统的旋转。不幸的是，基于经典算法和相位反冲的方法需要许多量子位，因此需要替代方法。

技术实现要素：

量子重复直到成功(RUS)乘法电路耦合到具有与函数变量的值相关联的相位的辅助量子位。在目标量子位输出处，如果耦合到辅助量子位的测量电路指示成功，则目标量子位相位是基于耦合到具有辅助量子位的RUS乘法电路的相位的结果。否则，校正电路被耦合来对目标量子位应用校正，并且重复乘法处理。齿轮箱(GB)和可编程辅助旋转(PAR)电路可以用于乘法，并且在附加的GB或PAR电路或其组合的所选误差限制内校正任何误差项。可以基于例如Taylor级数表示来估计函数，并且RUS电路被布置为提供对应于Taylor级数表示中的项的输入值的乘法。在一些示例中，多个辅助量子位耦合到RUS乘法电路，并且目标量子位相位基于应用到具有多个辅助量子位的RUS乘法电路的相位的结果。在一些情况下，目标量子位相位对应于应用到具有多个辅助量子位的RUS乘法电路的相位的结果的偶数或奇数幂，并且基于偶数或奇数幂是否将被选择，来选择齿轮箱或PAR电路计算。校正电路可以包括至少一个Clifford门。

下面参照附图阐述本公开的这些和其他特征和方面。

附图说明

图1示出了基于Bloch球上的旋转角度的编码。

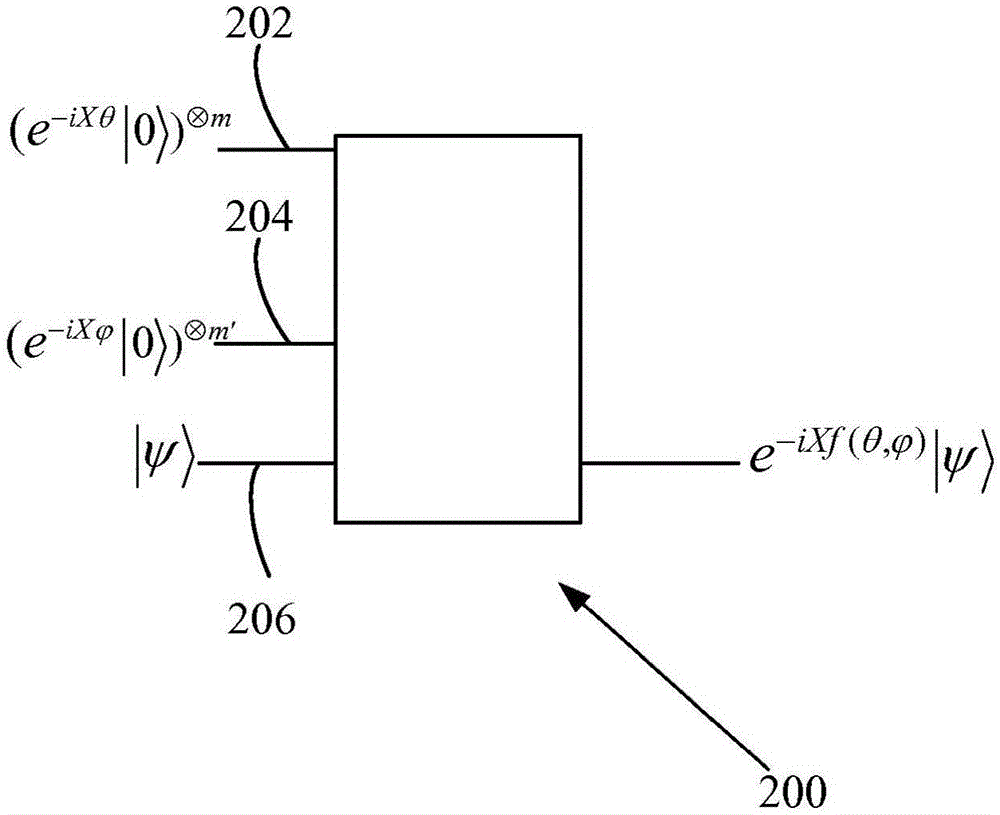
图2示出了代表性的重复直到成功(RUS)乘法电路。

图3示出了RUS电路的操作。

图4示出齿轮箱(GB)电路。

图5示出了可编程辅助旋转(PAR)电路。

图6A-图6B示出了用于使用RUS乘法电路来估计函数的值的方法。

图7示出了电路设计的方法。

图8A是列出各种量子算术电路的属性的表。

图8B是列出PAR电路的一些附加属性的表。

图9是列出所选择的乘法电路的属性的表。

图10示出了基于PAR电路的乘法电路。

图11示出了替代的乘法电路。

图12是用于在计算倒数中使用的Chebyshev近似的表。

图13示出了迭代地应用的齿轮箱电路的方波特性。

图14示出了利用齿轮箱电路产生的方波。

图15-图16示出了将齿轮箱方波函数拟合到网格以便拟合函数的方法。

图17示出了包括齿轮箱子电路的代表性PAR电路。

图18是其中可以实现所公开的方法的代表性计算环境的框图。

图19是包括经典和量子处理的代表性计算环境的框图。

具体实施方式

如本申请中和权利要求书中所使用的那样，除非上下文另有明确规定，否则单数形式“一”，“一个”和“该”包括复数形式。另外，术语“包括”是指“包含”。此外，术语“耦合”不排除在耦合的项之间存在中间元件。

本文所描述的系统、装置和方法不应被解释为以任何方式进行限制。相反，本公开单独地以及以彼此的各种组合和子组合的方式涉及了各种公开实施例的所有新颖的和非显而易见的特征和方面。所公开的系统、方法和装置不限于任何特定方面或特征或其组合，所公开的系统、方法和装置也不要求存在任何一个或多个具体优点或者解决问题。任何操作理论都是为了便于解释，但是所公开的系统、方法和装置不限于这样的操作理论。

尽管为了方便呈现而以特定的顺序次序描述了所公开的方法中的一些方法的操作，但是应当理解，除非下面阐述的特定语言需要特定的排序，这种描述方式包括重新布置。例如，顺序描述的操作在一些情况下可以进行重新布置或同时执行。此外，为了简单起见，附图可能未示出所公开的系统、方法和装置可以与其他系统、方法和装置结合使用的各种方式。另外，描述有时使用诸如“产生”和“提供”之类的术语来描述所公开的方法。这些术语是对所执行的实际操作的高级抽象。对应于这些术语的实际操作将取决于特定实现而变化，并且本领域的普通技术人员可以容易地辨别。

在一些示例中，数值、过程或装置被称为“最低”，“最佳”，“最小”等。应当理解，这样的描述旨在指示可以在许多使用的功能替代中进行选择，并且这样的选择不需要更好、更小或者优选于其他选择。

本文公开了允许使用数值近似的数值分析的量子计算方法和装置。代表性的数学分析可能需要基本的算术运算，例如整数或实数的加法、乘法和除法。其他分析还包括在一个或多个变量中的函数的评估、插值、微分和积分。在一些代表性示例中，公开了可以对在Bloch球表示中被编码为旋转状态的数字执行变换的量子计算算术方法和装置。所公开的电路和方法通常使用辅助量子位来表示输入变量的值。测量这些辅助量子位的状态以确定方法/电路成功。输出值被编码在这里被称为目标量子位的量子位上。

编码为Qubit旋转的数据

在量子计算机中实现算术和数值分析操作的常规方法通常使用多个量子位来将数字编码为量子位串。尽管可以使用这样的编码，但在所公开的示例中，通常将单个量子位用于编码。图1示出Bloch球的截面100，具体而言是YZ平面中的截面。向量102相对于Y轴具有围绕X轴(进入图1的页面)的旋转角度其中是多个变量θ₁，...，θ_k的函数。角度因此表示函数的值。在其他示例中，可以使用围绕其他轴的旋转。因此，旋转角度用于对数值进行编码，并且不需要多量子位编码。例如，围绕X轴的旋转幅度f(x)被应用到在状态|ψ>中的单个量子位，其中X是Pauli X算子，以对状态|ψ>上的值进行编码。

这种编码方法的一个优点是不需要是已知x的值：承诺输出e^-iφX的量子电路足够。因此，可以对幅度执行算术，或者等效地对旋转角执行算术，以替代对量子比特串进行算术。这可以大大减少执行某些量子计算所需的存储器。在一些示例中，量子数据包括在状态|ψ>中被初始化的仅一个量子位，并且要被应用到|ψ>的操作是围绕X轴的旋转，其中旋转角由函数给出，其中f是已知函数。换句话说，实现了酉(unitary)可以基于串联执行的旋转的和与差来对加法和减法操作进行编码。下面讨论用于旋转角度的乘法电路和方法。基于这些操作的实现，可以获得用于任意平滑函数的电路。图2是表示量子电路200的示意图，所述量子电路200接收对应于具有辅助量子位202，204的旋转角的编码值。目标量子位206耦合到电路200，以便在对应于的状态中被输出，其中f是变量的任意函数。

参考Clifford+T门集合描述所公开的示例。该集合包括Hadamard门，CNOT门和T门。这种门集合特别方便，但是所公开的方法不限于这种特定的门集合。数值通常被表示为旋转角，并且在一些示例中假设附加电路(不一定被描述)被布置为对量子位j＝1，...，k，执行单个量子位旋转，使得可以实现酉如上所指出，只要函数f是已知的，则旋转角不需要是已知的。

用于算术的重复直到成功(RUS)电路

重复直到成功(RUS)电路用于各种数学运算。RUS电路通常允许酉的概率执行，特别是取决于早期测量的结果的酉操作对于部分量子数据的条件应用。该执行被执行，使得每当计算的特定分支导致失败时，该失败是可检测的并且导致可校正的误差。通常方便的是任何这样的失败/误差可由Clifford门校正，但是也可以使用其他校正过程。如果任何这样的校正操作是相同的——即不需要校正，并且可以重复电路直到获得期望的测量结果(“成功”)，则是特别方便的。

以下公开了允许计算输入变量的幂及其结果的量子RUS电路。这些电路可以被组合以在Taylor级数近似中实现所选择的函数，表示为到领导阶(leading order)的、由PAR和齿轮箱电路所生成的函数的和。通常，为了获得选定的精度，通过使用PAR和齿轮箱电路对多项式进行近似而引入的误差是通过附加的PAR和齿轮箱电路来校正。在一些情况下，从图中省略了电路的RUS部分并且未对其进行讨论以便更好地示出在电路成功时如何执行算术过程。

一般来说，如图5中所定义的PAR电路不是RUS电路，因为可能存在不能使用Clifford电路来校正的误差结果(也参见图8A)。使用Childs等人在“Exponential improvement in precision for simulating sparse Hamiltonians”，arXiv：1312.1414(2013)中描述的不经意(oblivious)幅度放大技术，PAR电路可以通过与一个附加辅助量子位耦合而被转换成RUS电路。在下文中，我们使用术语PAR电路来表示PAR电路的两种变型。

图3示出了代表性的重复直到成功(RUS)电路300，其实现与预定函数的评估相关联的酉变换V。变换电路302在输入状态|ψ>和独立于输入状态|ψ>而准备的辅助状态上实现酉变换U。输入状态|ψ>和辅助状态中的任一个可以与一个或多个量子位相关联，但是在这里公开的大多数示例中，辅助状态|ψ>对应于单个量子位，并且辅助状态与被布置为向感兴趣函数提供输入的多个量子位相关联。在通过变换电路302应用酉变换U之后，由测量电路304测量保持所得到的辅助状态的寄存器。如果获得预定(期望的)测量结果x，则开关306被耦合，以便于将状态V|ψ>作为输出进行递送。如果没有获得预定(期望的)测量结果x，则开关306经由经典控制输入305而被耦合，以便于将对应于输入状态|ψ>的经处理状态|ψ′>递送到电路310。经处理状态|ψ′>与输入状态|ψ>由于Clifford或其他运算而不同。电路310将Clifford(或其他)运算Wx应用于经处理状态|ψ>，以便获得输入状态|ψ>，输入状态|ψ>然后被路由到电路302的输入。然后，电路再次处理输入状态|ψ>和辅助状态如图3所示，一旦成功，期望的输出状态V|ψ>可用。

可以方便地配置电路300，使得在测量电路304处的结果(0，...，0)的测量与成功相关联，但是成功也可以与其他结果相关联。在大多数示例中，假设输入量子位处于|0>状态，但是可以使用其他状态。通常，输入和辅助量子位被耦合到电路302，使得在成功时，基于输出状态V|ψ>，由辅助状态定义的变量的选定函数的值可用。辅助状态可以用多个量子位来定义，每个量子位代表不同的输入值。

RUS乘法电路

代表性的RUS电路接收一系列单个量子位旋转，并将该系列映射到单个量子位旋转。这些RUS电路优选地具有相对高的成功概率，并且在失败时可以被校正。在图4中示出了一个代表性电路400，其在本文中被称为齿轮箱(GB)电路。如图4所示，电路400包括旋转门406₁，...，406_k，其耦合到与旋转相关联的相应的量子位402₁，...，402_k，即，产生旋转可以包括与其他旋转相关联的附加量子位和旋转门，但是在图4中仅示出了两个量子位和相关联的旋转门。将处于状态|ψ>中的目标量子位405和旋转门406₁，...，406_k耦合到控制门410，控制门410包括-iX门，该-iX门被应用到由量子位402₁，...，402_k控制的量子位405。量子位402₁，...，402_k然后耦合到应用旋转的旋转门412₁，...，412_k，并且耦合到测量电路422₁，...，422_k。在电路400中，如果由测量电路422₁，...，422_k生成的测量结果对应于每个量子位402₁，...，402_k的状态|0>，则将旋转应用于目标量子位405。因此，状态|0>对应于成功；如果测量电路422₁，...，422_k返回与状态|1>相关联的值，则目标量子位的状态不对应于与旋转相关联的状态，并且目标量子位405再次被处理。

诸如图4的齿轮箱电路在成功时响应于辅助量子位相位而在目标量子位上产生以下旋转：

因此，对于相位的较小值，与目标量子位旋转相关联的Taylor级数是相位的偶次幂的函数，并且缺少奇次幂。因此，齿轮箱电路可以被用于产生对应于输入变量的偶数幂的量子位相位。在失败时，目标量子位的旋转对应于由单个Clifford门产生的旋转，其可以通过应用提供逆运算的门而被校正。奇数幂可以通过将输入相位移位π/4来获得，但是这样的移位会降低电路成功概率并且与缓慢收敛的Taylor级数相关联。

使用通过将输入相位移位π/4的这种想法，可以使用齿轮箱电路来实现乘法。以前，只知道齿轮箱可以被用来与由N.Wiebe和V.Kliuchnikov在“Floating Point Representations in Quantum Circuit Synthesis”，New J.Phys.15，093041(2013)所公开的平方运算结合相乘。

在图5中示出了替代电路500，本文中被称为可编程辅助旋转(PAR)电路。处于|0>状态中的辅助量子位501₁，...，501_k被耦合到相应的旋转门502₁，...，502_k，其又被耦合到控制门506。控制门506包括耦合到目标量子位503的Pauli-X旋转门508。一般的Bell状态电路的逆510被耦合到辅助量子位501₁，...，501_k，并且包括CNOT门512，其中选择的量子位(在这种情况下，辅助量子位501₁)针该CNOT门512用作控制；以及Hadamard门514，该Hadamard门514耦合到辅助量子位501₁。其他量子位可以被用作控制，并且该示例是为了方便说明。在由电路510处理之后，辅助量子位501₁，...，501_k被耦合到相应的测量电路520₁，...，520_k。如果所有测量电路520₁，...，520_k产生对应于概括Bell状态(在测量时在|1>状态中的所有辅助量子位或在|0>状态中的所有辅助量子位)的测量，则旋转存在于目标量子位503的相位上，如下所示：

+符号与对应于状态|0>^k+|1>^k和的测量的概括Bell状态相关联，并且-符号与对应于状态|0>^k-|1>^k差的测量的概括Bell状态相关联。对于任何其他测量结果，PAR电路是目标量子位上的标识操作。因此，PAR电路可以被用于产生与目标量子位上的输入变量的奇数幂相对应的相位。可以使用PAR电路的不经意幅度放大版本来消除与-1符号相关联的结果。

PAR和GB电路的各种组合是可能的。例如，可以利用图17的包括齿轮箱子电路1702的电路1700来实现arctan(tan²(φ₁)tan(φ₂))。

基于RUS的功能评估

在图6A中示出了用于评估任意函数f(x)的一般方法600。在602处，获得函数定义和一个或多个值(x)，在所述值处函数要被评估。为了方便起见，值x被示为单个值，但是f(x)可以是多个变量的函数，并且x然后表示针对多个变量中的每一个的值。在604处，使用合适的RUS齿轮箱和PAR电路将f(x)近似为f'(x)。在606处，定义差函数F(x)，并且在608处，使用RUS齿轮箱和PAR电路将差函数近似为F'(x)。然后f'(x)被设置为f'(x)+F'(x)。在610处，如果确定已经获得足够精确的估计，则在612处输出一个或多个估计值。否则，在606处定义附加差函数，并且继续估计，直到获得所选精度。在图6B中提供了这种方法的伪代码。

在图7中示出了定义用于函数的评估的量子电路的方法700。在702处，函数被近似为一个或多个输入变量的偶数和奇数幂。在704处，分配用于奇数幂项的电路，通常为PAR电路。在一些情况下，使用具有适当偏移的齿轮箱电路，但是如上所述，没有偏移的实现往往更简单。在706处，定义用于偶数项的电路，通常是齿轮箱电路。在一些情况下，使用具有适当偏移的PAR电路，但是如上所述，没有偏移的实现往往更简单。在710处，所选择的PAR和齿轮箱电路耦合在一起以限定用于所选择的功能的电路。

增强RUS电路精度

如上所讨论的，PAR和GB电路二者都基于输入变量的三角函数而产生量子位相位。对于小的输入变量值，电路输出对应于输入值的结果或结果的平方，忽略高阶项。为了更准确地获得这样的结果，可以减少或消除这些高阶项的贡献。PAR和GB电路以及加法电路的属性在图8A中示出。如图8A所示，PAR和GB电路比结果幂的简单结果具有更复杂的输出。成功的概率被列出，并且在失败的情况下使用的校正电路也被记录。图8B列出了齿轮箱电路的一些附加属性。

一种校正PAR和GB电路输出的方法是使用附加的PAR或GB电路来估计校正项，使得可以对目标量子位进行适当的相位校正。使用这种校正的电路包括附加的量子位，并且替代方法是优选的。使用单个PAR电路乘以两个输入的乘法产生具有O(x⁴)误差的结果。为了方便，将产生误差O(xⁿ)的电路称为Mⁿ。PAR电路单独是一个M⁴电路。如果x，则Taylor级数代表PAR(ax，bx)的输出(即，arctan(x)＝x-x³/3+…和tan(x)＝x+x³/3+…)，则：

可以使用GB(ax)＝a²x²+O(x⁴)并且然后再应用两个更多PAR电路串联来消除O(x⁴)中的误差项，并且Taylor展开结果为：

PAR(ax，bx)-PAR(ax，bx，GB(ax)，arctan(1/3))-PAR(ax，bx，GB(bx)，arctan(1/3))＝abx²+O(x⁶)虽然这种方法起作用，但是下面公开的更简单的方法通常更方便实现。

PAR(ax，bx)中的每个项由至少一个a和b组成，因此(1-a²x²/3-b²x²/3)可以乘以PAR(ax，bx)以实现期望的结果。要做到这一点，一个有效的方法要注意：

tan(x+π/4)＝1+2x+O(x²)。

因此，对于任何分析函数f(x)

arctan(tan(ax)tan(bx)tan(f(x)+π/4))＝arctan(tan(ax)tan(bx)+2f(x)tan(ax)tan(bx)+O(f(x))²)。

在图9所示的M⁶电路中使用的f(x)的选择是：

这与PAR电路误差一起显示：

arctan(tan(ax)tan(bx)tan(f(x)+π/4))

＝arctan(tan(ax)tan(bx)-a³bx⁴/3-b³ax⁴/3+O(x⁶))

＝arctan(tan(ax)tan(bx))-a³bx⁴/3-b³ax⁴/3+O(x⁶)

＝abx²+O(x⁶)。

因此，M⁶使用PAR电路给出了两个数的结果的六阶近似。可以类似地获得用于其他阶次的电路。π/4相移降低了成功的概率，并且仅在需要时使用。

图9是总结了以这种方式获得的M⁴，M⁶和M⁸的电路设计以及实现所需的量子位数的表格。常数是和针对宽度对电路进行优化，并且意指电路在PAR电路中从右向左执行，以允许最左侧的量子位用作其右侧出现的用于齿轮箱操作的辅助。

图10示出了M⁴电路1000，其包括被耦合到应用了输入值的辅助量子位1004，1006的PAR电路1002。目标量子位1008的状态|ψ>由PAR电路1002(在成功时)旋转以产生输出状态在失败的情况下将输出状态耦合到输入，被示为1010，但是未示出一个或多个校正门。图11示出了M⁶电路1100，其包括GB电路1102，1104、由恒定门1106的旋转、和在目标量子位1112上提供结果作为相位(旋转)的PAR电路1110。

所公开的方法和电路允许使用乘法和加法运算实现大多数函数的量子计算。在一些情况下，使用Taylor级数(或其他级数展开)，并且将函数变量的各种结果映射到适当的电路，比如PAR和GB电路的组合。可以基于优选的误差限制来选择特定的设计以减少量子位的总数，或者可以基于其他考虑来选择。还可以构造用于整数乘法、脉动进位(carry-ripple)乘法和表查找乘法器的量子电路。

用于倒数(Reciprocal)评估的RUS电路

在一些应用中，对于作为量子状态存储的一些值α，要确定变量的倒数，即要获得形式e^-iX/a的旋转。一种确定倒数的方法是基于Newton方法。该方法对于良好的初始估计进行二次收敛，并且仅需要乘法和加法。特别地，如果x_n是对倒数的值的近似，则牛顿法提供新的近似该过程可以在合理的猜测(例如)处开始重复并迭代，直到误差足够小。

基于Chebyshev近似和二项式方法，也可以使用用于计算倒数的其他方法。这两种方法中的第一步通常涉及重新缩放a，以避免在Newton方法的直接应用中出现的发散系数。这种重新缩放可以被表示为

其中可以引入新的变量其中y∈[0，1/2]。此变量是使用在幂级数展开的自然数，因为它严格小于1/2。换句话说，发现y的幂中的幂级数近似为合适的方法基于Taylor级数、Chebyshev多项式和二项式除法算法。由于慢收敛，Taylor级数趋于为该应用提供差的准确度。

使用Chebyshev多项式展开，找到倒数的问题被减少到实现多项式的问题。这可以通过使用上面提供的乘法公式来实现。重新缩放的倒数1/(1-y)的三个最低阶Chebyshev近似值在图12的表中给出。通过使用齿轮箱电路实现平方，可以避免PAR电路。

二项式方法是用于计算倒数的替代方法。二项式方法基于展开

其可以被实现为一系列乘法。

函数的基于RUS的方波表示

当迭代地应用时，齿轮箱(和PAR)电路近似方波。图13示出了齿轮箱电路的三个迭代应用，其示出了这些迭代如何趋近方波。图14示出了具有由系数a₁，a₂，a₃确定的不同周期的齿轮箱方波。该行为可以被用来估计函数值如下。参考图15，在1502处在点的网格上评估函数。在1504处将方波拟合到网格点，并且在1506处，确定用于每个方波的系数。该过程在图16的伪代码中被更详细地描述。

经典和量子计算环境

图18和以下讨论旨在提供其中可以实现所公开的技术的示例性计算环境的简要的一般描述。尽管不是必需的，但是在由个人计算机(PC)执行的诸如程序模块之类的计算机可执行指令的一般上下文中描述所公开的技术。通常，程序模块包括执行特定任务或实现特定抽象数据类型的例程，程序，对象，组件，数据结构等。此外，所公开的技术可以用其他计算机系统配置来实现，包括手持设备，多处理器系统，基于微处理器或可编程消费电子产品，网络PC，小型计算机，大型计算机等。所公开的技术还可以被实践在分布式计算环境中，其中由通过通信网络链接的远程处理设备来执行任务。在分布式计算环境中，程序模块可以位于本地和远程存储器存储设备二者中。

参考图18，用于实现所公开的技术的示例性系统包括以示例性常规PC 1800的形式的通用计算设备，包括一个或多个处理单元1802，系统存储器1804和系统总线1806，所述系统总线1806将包括系统存储器1804的各种系统组件耦合到一个或多个处理单元1802。系统总线1806可以是若干类型的总线结构中的任一种，包括存储器总线或存储器控制器、外围总线和使用各种总线架构中的任何一种的局部总线。示例性系统存储器1804包括只读存储器(ROM)1808和随机存取存储器(RAM)1810。包含帮助在PC 1800内的元件之间传送信息的基本例程的基本输入/输出系统(BIOS)1812存储在ROM 1808中。

如图18所示，用于实现诸如乘法和函数估计之类的RUS算术运算的计算机可执行指令被存储在存储器部分1816中，并且包括用于例如求解整数方程、评估和求解标准方程以及用于确定r值的随机抽样的指令。此外，存储器部分1818存储如上所公开的RUS乘法电路定义、描述、布置和方法。还存储有用于接收旋转角度和精度以及通信电路定义的计算机可执行指令。

示例性PC 1800还包括一个或多个存储设备1830，例如用于读写硬盘的硬盘驱动器，用于读写可移动磁盘的磁盘驱动器，以及用于读写可移动光盘(例如CD-ROM或其他光学介质)的光盘驱动器。这样的存储设备可以分别通过硬盘驱动器接口、磁盘驱动器接口和光驱动器接口连接到系统总线1806。驱动器及其相关联的计算机可读介质提供了用于PC 1800的计算机可读指令、数据结构、程序模块和其他数据的非易失性存储。也可以在示例性操作环境中使用诸如磁带盒，闪存卡，数字视频盘，CD，DVD，RAM，ROM等等之类的可以存储可由PC访问的数据的其他类型的计算机可读介质。

包括操作系统、一个或多个应用程序、其他程序模块和程序数据的多个程序模块可以被存储在存储设备1830中。量子合成和用于获得这种合成的指令的存储可以被存储在存储设备1830中或者附加地存储在存储器1804中。用户可以通过一个或多个输入设备1840(例如，键盘和诸如鼠标的指示设备)将命令和信息输入到PC 1800。其他输入设备可以包括数字照相机，麦克风，操纵杆，游戏垫，卫星天线，扫描仪等。这些和其他输入设备通常通过耦合到系统总线1806的串行端口接口连接到一个或多个处理单元1802，但是可以通过其他接口进行连接，例如并行端口，游戏端口或通用串行总线(USB)。监视器1846或其他类型的显示设备也经由诸如视频适配器之类的接口而被连接到系统总线1806。可以包括其他外围输出设备，诸如扬声器和打印机(未示出)。在一些情况下，用户接口是显示器，使得用户可以输入用于合成的电路，并验证成功的合成。

PC 1800可以使用对于一个或多个远程计算机(诸如远程计算机1860)的逻辑连接在联网环境中操作。在一些示例中，包括一个或多个网络或通信连接1850。远程计算机1860可以是另一个PC，服务器，路由器，网络PC或对等设备或其他公共网络节点，并且典型地包括上面相对于PC 1800描述的许多或所有元件——尽管只有存储器存储设备1862已经在图2中被示出。个人计算机1800和/或远程计算机1860可以被连接到逻辑局域网(LAN)和广域网(WAN)。这样的网络环境在办公室、企业级计算机网络、内联网和因特网中是常见的。

当在LAN联网环境中使用时，PC 1800通过网络接口连接到LAN。当在WAN联网环境中使用时，PC 1800通常包括调制解调器或其他用于通过WAN(例如因特网)建立通信的装置。在联网环境中，相对于个人计算机1800描述的程序模块或其部分可以被存储在远程存储器存储设备或LAN或WAN上的其他位置中。所示出的网络连接是示例性的，并且可以使用在计算机之间建立通信链路的其他手段。

参考图19，用于实现所公开的技术的示例性系统包括计算环境1900，其中编译成编织图案电路与消耗编译的电路的量子处理相分离。该环境包括量子处理单元1902和一个或多个监控/测量设备1946。量子处理器执行由经典编译器单元1920利用一个或多个经典处理器1910预编译的量子电路。诸如用于乘法、函数估计或其他过程的RUS电路1903之类的预编译量子电路经由量子总线1906被下载到量子处理单元中。

如图19所示，编译是将量子算法的高级描述翻译成量子电路序列的过程。这样的高级描述可以根据情况被存储在利用一个或多个存储器和/或存储设备1962的计算环境1900外部的一个或多个外部计算机1960上，然后根据需要经由一个或多个通信连接1950而被下载到计算环境1900中。备选地，经典编译器单元1920被耦合到经典处理器1910和RUS算术程序库1921(包含实现上述方法所必需的一些或所有过程)、以及RUS电路库1903(存储用于乘法、级数展开、倒数确定或方波表征的编译电路)。

已经参考所示实施例描述和示出了本发明的原理，应当认识到，在不脱离这些原理的情况下，可以在布置和细节上修改所示出的实施例。例如，以软件示出的所示实施例的元件可以用硬件实现，反之亦然。此外，来自任何示例的技术可以与任何一个或多个其他示例中描述的技术进行组合。在这些部分中具体涉及的替代方案仅仅是示例性的，并且不构成所有可能。