信息处理装置、信息处理方法和计算机可读存储介质与流程
本发明涉及一种信息处理装置、信息处理方法、和存储用于实现该装置和该方法的程序的计算机可读存储介质,并且具体地,涉及用于通过多维度数据来有效地执行搜索的一种信息处理装置、信息处理方法、和计算机可读存储介质。
背景技术:
当在多维度空间中存在许多点时,寻找包括在指定矩形范围中的点被称为“正交范围搜索”。例如,当d表示维度的数量时,可以使用d个坐标的组合来用p=(p1,p2,...,pd)表示存在于具有d维度的多维度空间中的点。此处,由[lkq,uqk]来表示相对于每个维度k的范围,并且考虑了由q=[lq1,uq1]×[lq2,uq2]×...×[lqd,lqd]表示的d维度矩形范围。将该矩形范围称为查询区域,并且正交范围搜索的目的在于搜索包括在该查询区域q中的点p,即满足
这种正交范围搜索在处理地理信息的应用中以及在多维度数据分析中起着重要的作用。下面示出了具体的示例。
例如,可以由作为两个值的组合的二维数据“(纬度,经度)”来表示餐馆在地图上的位置。在这种情况下,通过使用正交范围搜索,可以搜索纬度在138度至139度范围内并且经度在35度至36度范围内的所有餐馆。
同样,例如,可以通过使用三维数据“(年龄,身高,年收入)”来表示关于公司员工的统计数据。在这种情况下,通过使用正交范围搜索,可以搜索年龄在30至40范围内、身高在170cm至180cm范围内、并且年收入在500万日元至600万日元范围内的所有员工。
此外,正交范围搜索存在各种变型,该各种变型的不同之处在于返回的搜索结果是什么。报告查询和聚合查询是这些变型的示例。
首先,报告查询是返回包括在查询区域中的所有点的列表的正交范围搜索。包括在查询区域中的点的数量被称为命中计数。报告查询返回具有与命中计数成比例的大小的列表,并且因此,报告查询不适用于分析命中计数被预期为较大的大规模数据。例如,当包括数千万个点时,报告查询输出所有数千万个点。
因此,在大规模数据分析的情况下,与返回包括在查询区域中的所有点的列表相比较,返回这些点的聚合结果的聚合查询更为重要。在各种聚合查询中最具代表性的查询是计数查询。
该计数查询是一种返回包括在查询区域中的点的数量的正交范围搜索。除了计数查询之外,当对每个点赋予权重时,存在以下查询,例如:返回包括在查询区域中的点的权重的总和的总和查询;返回权重的平均值的平均查询;返回权重的最大值的最大值查询。
k-d树被已知为可以用于正交范围搜索的代表性数据结构(例如,见非专利文献1)。可以由o(n)来表示k-d树的大小,即,线性大小。同样,已知的是,使用k-d树的正交范围搜索的最差时间复杂度为o(n(d-1)/d)。注意,n表示数据集的数量,并且d表示维度的数量。在具有线性大小的常规已知数据结构的时间复杂度中,通过使用k-d树实现的最差时间复杂度o(n(d-1)/d)是最佳的时间复杂度。
如果将正交范围搜索应用于具有大于o(n)的超线性大小的数据结构,则可以改进计算时间(时间复杂度)。具有这种超线性大小的数据结构的示例是被称为“范围树”的数据结构。
还可以通过使用称为“小波树”的二维数据结构来实现正交范围搜索(例如,见非专利文献1)。如果是这种情况,则在二维空间内执行搜索,并且时间复杂度为o(logn)。注意,在非专利文献1中描述了使用k-d树和小波树的上述正交范围搜索的细节。
引文列表
非专利文献
非专利文献1:menghe,“succinctandimplicitdatastructuresforcomputationalgeometry(针对计算几何学的简明和隐式的数据结构)”,lecturenotesincomputersciencevolume8066“space-efficientdatastructures,streams,andalgorithms(空间有效的数据结构、流和算法)”,第216-235页,2013,springerberlinheidelberg,isbn978-3-642-40272-2。
技术实现要素:
技术问题
按照这种方式,各种数据结构可用于实现正交范围搜索。然而,在实践中,存在以下问题。首先,在通过使用k-d树来实现正交范围搜索的情况下,存在如下问题:其中,可实现的最差时间复杂度o(n(d-1)/d)随着以下字母中的一个或者两个的增加而增加:表示数据集的数量的n,和表示维度的数量的d。
同样,如果通过使用具有超线性大小的数据结构来实现正交范围搜索,则虽然与通过使用k-d树来实现正交范围搜索的情况相比较可以改进计算时间,但是存在如下问题:其中,具有超线性大小的数据结构在大小上过大,因此在实际应用中使用该数据结构是困难和不实际的。
此外,如果通过使用小波树来实现正交范围搜索,则由于小波树仅适用于二维数据,因此,存在如下问题:其中,不能通过具有大于或者等于3的期望维度数的数据结构来执行搜索。
本发明的目的的一个示例是解决上述问题并且提供可以通过使用具有线性大小的数据结构来以与k-d树的情况相比较更快的速度实现相对于期望维度的正交范围搜索的一种信息处理装置、信息处理方法、和计算机可读存储介质。
技术方案
为了实现上述目的,根据本发明的一个方面的信息处理装置是处理表示在多维度空间中包括的点的集合的数据结构的信息处理装置,该信息处理装置包括:
搜索单元,当将特定多维度区域指定为查询区域时,该搜索单元在构建数据结构的多维度区域内指定表示为在以特征值前缀开始的区域与相对于相应维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域,并且输出作为包括在与指定区域对应的数据结构中的区间的选定的区间,特征值前缀是从点的特征值的位表示获得的前缀,并且坐标前缀是相对于特定维度从点的坐标的位表示获得的前缀;以及
聚合单元,该聚合单元通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
同样,为了实现上述目的,根据本发明的一个方面的信息处理方法是用于处理表示在多维度空间中包括的点的集合的数据结构的信息处理方法,该信息处理方法包括:
(a)步骤:当将特定多维度区域指定为查询区域时,在构建数据结构的多维度区域内指定表示为在以特征值前缀开始的区域与分别相对于维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域,特征值前缀是从点的特征值的位表示获得的前缀,并且坐标前缀是相对于特定维度从点的坐标的位表示获得的前缀;
(b)步骤:输出作为包括在与在所述步骤(a)中指定的区域对应的数据结构中的区间的选定的区间;以及
(c)步骤:通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
此外,为了实现上述目的,根据本发明的一个方面的计算机可读存储介质是存储用于使计算机执行信息处理以处理表示在多维度空间中包括的点的集合的数据结构的程序的计算机可读存储介质,该程序使计算机执行:
(a)步骤:当将特定多维度区域指定为查询区域时,在构建数据结构的多维度区域内指定表示为在以特征值前缀开始的区域与分别相对于维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域,特征值前缀是从点的特征值的位表示获得的前缀,并且坐标前缀是相对于特定维度从点的坐标的位表示获得的前缀;
(b)步骤:输出作为包括在与在所述步骤(a)中指定的区域对应的数据结构中的区间的选定的区间;以及
(c)步骤:通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
发明效果
如上所述,根据本发明,可以通过使用具有线性大小的数据结构来以与k-d树的情况相比较更快的速度实现相对于期望维度的正交范围搜索。
附图说明
图1是示出了在二维空间中的坐标和z值的示例的示意图。
图2是示出了根据本发明的实施例的信息处理装置的整体构成的框图。
图3是示出了根据本发明的实施例的信息处理装置的具体构成的框图。
图4是示出了在本发明的实施例中使用的z值序列和坐标序列的示例的示意图。
图5是示出了在本发明的实施例中使用的小波树的示例的示意图,其中,图5的(a)和(b)示出了分别具有不同维度数量的小波树。
图6是示出了根据本发明的实施例的信息处理装置的操作的流程图。
图7是示出了用于递归地执行正交范围搜索的函数“range_search(v,q)”的操作的流程图。
图8是示出了用于计算z值搜索节点v的左子节点和右子节点的函数“get_children(v)”的操作的流程图。
图9是示出了在图7中示出的函数“range_search_1d(v,q)”的操作的示意图。
图10是示出了在图9中示出的函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”的操作的示意图。
图11是示出了在二维情况下的搜索节点的数量变化和包括维度数变化的示意图。
图12是示出了在本发明与传统方案之间针对时间复杂度的比较的示意图。
图13是示出了根据本发明的实施例的实现信息处理装置的计算机的示例的框图。
具体实施方式
本发明的原理
首先,下面将通过使用典型的k-d树作为示例来描述本发明的基本原理。
首先,k-d树是用于处理多维度数据的二叉搜索树。k-d树的特征在于,相对于从维度1到维度d的每个维度,将整个空间按顺序地划分为两个空间。k-d树的树结构表示空间的递归划分,并且为二叉搜索树的每个节点分配有局部区域。在本说明书中,将分配给节点v的局部区域称为该节点的“覆盖区域”。
此外,k-d树的每个节点可以保留关于包括在节点的覆盖区域中的点的统计量。例如,当期望高速计算出计数查询时,将包括在每个节点的覆盖区域中的点的数量存储在节点中。
按照以下方式来实现使用k-d树的正交范围搜索。首先,针对用作起始点的根节点,确定分配给子节点的覆盖区域是否与查询区域重叠。仅在覆盖区域与查询区域重叠时才发生向子节点的移动,并且重复地执行这种操作。向子节点的移动与相对于特定维度将覆盖区域划分为两个区域对应。如果分配给节点的覆盖区域完全包括在查询区域中,则将存储在节点中的关于包括在覆盖区域中的点的统计量添加至输出结果。
在使用k-d树的搜索中,如上所述,针对多个节点划分给定查询区域,从而使得覆盖区域包括在查询区域中,并且通过针对包括在相应覆盖区域中的点,对存储在节点中的统计量进行求和,来获得搜索结果。k-d树的最差时间复杂度o(n(d-1)/d)表示用于执行该空间划分所需要的节点的数量。如果采用了参照节点来执行空间划分的这种方法,则不可能实现比最差时间复杂度o(n(d-1)/d)更好的时间复杂度。
相反,根据本发明,不参照节点来执行划分,而是参照基于存在于多维度空间中的点的坐标计算出的特征值的前缀来执行。更具体地,首先,针对每个点定义称为“z值”的特征值,并且然后找到与查询区域对应并且特征值以特定前缀开始的区域。其次,在由此找到的区域中,搜索包括在查询区域中、并且相对于特定维度的坐标以特定前缀开始的局部区域。根据本发明,这种部分区域不作为树结构的节点来获得,而是作为包括在与树结构的节点对应的坐标子序列中的区间来获得。
如上所述,根据本发明,不参照节点来划分查询区域。根据本发明,通过使用在由前缀定义为点的特征值的覆盖区域与由前缀相对于每个维度定义为点的坐标的覆盖区域之间共享的局部区域的集合来划分查询区域。因此,根据本发明,与利用k-d树进行搜索的情况不相似,可以降低用于划分查询区域所需要的时间复杂度,并且可以按照比利用k-d树进行搜索的情况更快的速度实现正交范围搜索。
本说明书中采用的概念
下面描述了本说明书中采用的各种概念。在本说明书中,用整数[0,n-1]来表示所有点的坐标pi。而且,用具有二进制长度l=ceil(logn)的位来表示这些整数。注意,ceil()表示取顶函数。log表示二进制对数函数。
例如,当n=8时,用整数[0,7]来表示所有坐标,并且用l=ceil(logn)=3(位)来表示二进制长度l。换句话说,可以由0="000"、1="001"、2="010"、3="011"、4="100"、5="101"、6="110"、或者7="111"来表示二进制长度l。
然而,本发明还可应用于坐标不是用整数表示的普通多维度空间。例如,通过采用转换为秩空间,可以将n个点(其中,n是给定的实数)转换为在范围[0,n-1]内的整数坐标,并且可以通过使用该坐标来实现正交范围搜索。因此,通过进行这种转换为秩空间,可以将本发明应用于用实数表示的普通多维度空间。注意,例如,在上述非专利文献1中公开了转换为秩空间。
同样,如果将值表示为由"1"和"0"组成的二进制数,则即使没有执行针对秩转换的转换,也可以采用本发明。换句话说,当数据集的数量为n时,本发明还可应用于具有在范围[0,n-1]以外的坐标值的数据集。在本说明书中,将坐标的值的范围限制为范围[0,n-1]以从逻辑上分析时间复杂度。然而,在实践中,可以在未将坐标的值的范围限制为范围[0,n-1]的情况下采用本发明。
而且,在本说明书中,使用称为“前缀”的概念。前缀是从表示为二进制的整数中取出的高阶位。在本说明书中,将整数的较高阶h位的前缀表示为1、0、和*的组合,其中,"1"和"0"的数量总共为h,并且"*"的数量为l-h。*是通配符,且指示其可以是1或者0。如果整数以特定前缀开始,则该整数包括在特定的连续范围中。
例如,可以假设整数由长度为l=3的位序列来表示。如果是这种情况,则长度为1的前缀"0**"与四个值对应,即,"000"、"001"、"010"、和"011"。换句话说,前缀与作为整数值的范围的范围["000","011"]=[0,3]对应。类似地,长度为2的前缀"01*"与两个值(即,"010"、和"011")对应,并且与值的范围["010","011"]=[2,3]对应。长度为l(=3)的前缀仅与一个整数对应。
在本说明书中,以下表示用于序列。例如,当存在长度为n的序列a时,a[0]表示a的第一个元素,并且a[n-1]表示a的最后一个元素。而且,a[i,j]表示在a中从位置i处的元素a[i]到位置j处的元素a[j]的区间,并且a[i,j]表示排除端部j的区间。
接下来,将描述称为z排序的空间填充曲线。空间填充曲线是通过在d维度空间中的所有点的曲线。使用空间填充曲线,可以将在d维度空间中的位置转换为在一维空间中的位置。例如,通过使用z排序,可以将由d坐标定义的点p(p1,p2,...,pd)转换为称为z值的一维值。
下面示出了对z值的定义。当由长度为l的位来表示pi时,将z值表示为长度为d*l的位序列,在该位序列中,交替地包括每个指示相对于对应维度的点p的坐标pi的位。换句话说,z值是由在多维度空间中的点的坐标指定的特征值。首先,采集坐标p1、p2、...、pd的相应最高阶位并且对其进行级联。其次,采集坐标p1、p2、...、pd的相应第二最高阶位并且对其进行级联。在重复该操作l次之后,按照该次序来对由此获得的位序列进行进一步级联。按照这种方式而最终获得的位序列是z值。
此处,参照图1描述了z值的具体示例。图1是示出了在二维空间中的坐标和z值的示例的示意图。在图1中,纵轴指示维度1,并且横轴指示维度2。分别写在正方形中的每个位序列(二进制数)指示从相对于维度的相应坐标中获得的z值。
具体地,在图1中示出的示例中,用l=3位来表示在d(=2)维空间中的每个点p。在这种情况下,用d*1=2*3=6位来表示与点p对应的z值。例如,当p=(p1,p2)=("000","111")=(0,7)时,与该点p对应的z值为z="010101"。
接下来,将描述应用于z值的前缀的重要特性。在下面的描述中,将从表示z值的位表示获得的前缀称为“z值前缀”,并且将从表示相对于维度的相应坐标的位表示获得的前缀称为“坐标前缀”。
通过反向应用从相对于维度的坐标到z值的转换,可以将z值前缀πz划分为与每个维度对应的d坐标前缀{πk}(1≤k≤d)的组。换句话说,针对满足1≤k≤d的维度k,可以通过以d位为间隔来采集位(即,第k个位、第(k+d)个位、第(k+2d)个位,第(k+2d)位等)并且对这些位进行级联,而获得相对于维度k的坐标前缀πk。将该前缀称为相对于维度k与πz对应的坐标前缀。
针对相对于维度k的坐标前缀πk,用[lπk,uπk]来表示以πk开始的相对于维度k的坐标的区间。此处,定义πk的覆盖区域c(πk),以使其仅相对于维度k被限制于区间[lπk,uπk],并且相对于其它维度不进行限制。换句话说,满足c(πk)=[0,n-1]×...×[0,n-1]×[1πk,uπk]×[0,n-1]×...×[0,n-1]。
同样,将z值前缀πz的覆盖区域c(πz)定义为c(πz)=c(π1)∩c(π2)∩...∩c(πd)=[lπ1,uπ1]×[uπ2]×...×[lπd,uπd]。当点p包括在c(πz)中时,保证点p的z值始终以πz开始。这是因为坐标pk以坐标前缀πk开始。
例如,可以假设给出了长度为3的z值前缀πz="011***"。如果相对于该前缀来执行从z值到相对于维度的相应坐标的反向转换,则将前缀划分为相对于维度1长度为2的坐标前缀π1="01*"、和相对于维度2长度为1的坐标前缀π2="1**"。
此处,满足[lπ1,uπ1]=["010","011"]=[2,3],并且满足[lπ2,uπ2]=["100","111"]=[4,7],并且满足c(πz)=[2,3]×[4,7]。在图1中示出了这种关系。如可以通过图1看出的,在相对于维度1的区域c(π1)与相对于维度2的区域c(π2)之间重叠的区域c(π1)∩c(π2)与c(πz)一致。包括在c(πz)中的所有z值以πz开始。
最后,将描述对“包括维度数”的定义,该“包括维度数”是用于描述终止空间划分的条件所需要的。当相对于维度k满足以下包括条件时,可以说“覆盖区域包括在相对于维度k的查询区域中”。
包括条件:lkq≤lπk并且uπk≤uqk。
此外,当覆盖区域相对于在d个维度中的h个维度而包括在查询区域中时,可以说“覆盖区域的包括维度数为h”。如果包括维度数为d,即,如果覆盖区域相对于所有维度而包括在查询区域中,则可以说,覆盖区域完全包括在查询区域中。
实施例
接下来,将参照图1至图13来描述根据本发明的实施例的信息处理装置、信息处理方法、和程序。
装置构成
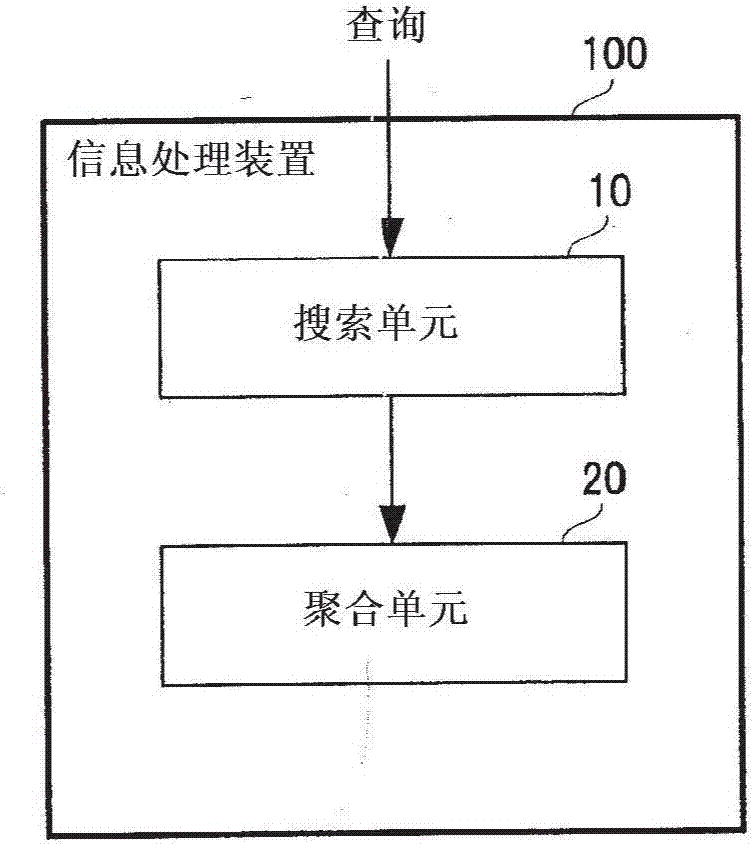
首先,将参照图2来描述根据本发明的实施例的信息处理装置的整体构成。图2是示出了根据本发明的实施例的信息处理装置的总体构成的框图。在图2中示出的根据本实施例的信息处理装置100是处理表示在多维度空间中的点的集合的数据结构的装置。如在图2中示出的,信息处理装置100包括搜索单元10和聚合单元20。
当将特定多维度区域指定为查询区域时,在这些单元中的搜索单元10起作用。在这种情况下,在构建数据结构的多维度区域内,搜索单元10指定表示为在以特征值前缀开始的区域与分别相对于维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域。
注意,“特征值前缀”与上述z值前缀含义相同,并且是从表示点的特征值(z值)的位表示获得的前缀。如上所述,“坐标前缀”是相对于特定维度从表示点的坐标的位表示获得的前缀。
接着,搜索单元10输出作为包括在与指定区域对应的数据结构中的区间的选定的区间。聚合单元20通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
如上所述,如果采用信息处理装置10,则基于在由特征值前缀确定的区域与由相对于维度的相应坐标前缀确定的区域之间共享的区域来划分输入查询区域,并且因此,与利用k-d树进行搜索的情况搜索相比较,可以降低用于划分查询区域所需要的时间复杂度。因此,根据信息处理装置10,可以通过使用具有线性大小的数据结构来以与利用k-d树进行搜索的情况相比较更快的速度实现相对于期望维度的正交范围搜索。
接下来,将参照图3来更具体地描述根据本实施例的信息处理装置100的构成。图3是示出了根据本发明的实施例的信息处理装置的具体构成的框图。
如在图3中示出的,除了搜索单元10和聚合单元20之外,根据本实施例的信息处理装置100还包括:输入接收单元30、输出单元40、和存储单元50。在这些单元中,输入接收单元30接收查询区域的外部输入,并且将查询区域输出至搜索单元10。
存储单元50存储表示在多维度空间中的点的集合的数据结构51。利用维度数量为d的d个小波树来构建根据本实施例的数据结构51。每个小波树与一个维度对应。
下面描述了d个小波树的结构。首先,按照升序来存储在多维度空间中的n个点的z值(见图1)的序列(特征值序列),并且将该序列表示为z。此外,按照与z值的升序相同的次序来排列与z值对应的点p,并且因此构建点p的序列p。然后,取出相对于维度k构建序列p的点的坐标,并且按照与前面提到的次序相同的次序来排列如此取出的坐标。将由此获得的序列表示为pk。将该序列pk称为坐标序列。注意,序列z、序列p、和序列pk都是长度为n的序列。
针对满足0≤i<n的i,z值z[i]和坐标pk[i]与相同的点p[i]对应。同样,在范围1≤k≤d内,相对于坐标序列pk来针对每个维度k生成小波树。要生成的小波树的数量为d,并且将d个小波树的集合表示为w={wk}。利用d个小波树的集合w来构建数据结构51。
此处,除了上述图1之外,将参照图4和图5来描述d小波树的具体示例。在下面的描述中,假设维度的数量为2。图4是示出了在本发明的实施例中使用的z值序列和坐标序列的示例的示意图。图5是示出了在本发明的实施例中使用的小波树的示例的示意图,其中,图5的(a)和(b)示出了分别具有不同维度数量的小波树。
首先,如在图1中示出的,假设在正方形中的八个圆圈表示在二维空间中的点p。在这些示例中,满足n=8,并且将每个点表示为在[0,7]×[0,7]=64个栅格上的点。例如,用(5,2)=("101","010")表示的点的z值为"100110"=38。在这点上,写在圆圈中的数字是按照升序来排列对应的z值时的次序。
图4示出了三个表,并且在这些表中的上面一个表示出了由z值组成的序列z。同样,在图4中,由z值组成的序列z与在图1中示出的八个点对应。中间的表和下面的表示出了与由z值组成的序列z对应的坐标序列pi。在这些示例中,维度的数量为两个,并且因此,中间的表示出了坐标序列p1,并且下面的表示出了坐标序列p2。
在每个表中,第一行示出了序列的索引i,并且第二行示出了与索引对应的整数。第三行和后续行示出了整数的位表示。例如,在图1中由(5,2)表示的位置处的z值38位于索引4的位置。因此,满足z[4]=38、p1[4]=5,并且p2[4]=2。
将与相对于维度i的坐标序列pi对应的小波树定义为如下的二叉树。注意,小波树是深度为l的二叉树。在该树结构中,在左侧上从父到子的边缘与位0对应,并且在右侧上从父到子的边缘与位1对应。
首先,假设小波树的根节点位于深度0处,并且与长度为0位的坐标前缀对应。还假设位于小波树中的深度h处的节点v与可以通过对出现在从根到节点的路径中的h位进行级联而获得的h位坐标前缀π对应。位于深度l处的节点都是叶节点。叶节点与由可以通过对出现在从根到节点的路径中的l位进行级联而获得的l位表示的一个整数对应。
此外,位于小波树中的深度h处并且与坐标前缀π对应的节点v与坐标序列pi中的子序列pi(π)对应。注意,pi(π)是从坐标序列pi中取出的子序列,从而使得按照与原始次序相同的次序来保持以坐标前缀π开始的所有整数。在本说明书中,将原始pi和针对坐标前缀π取出的子序列pi(π)分别称为“坐标序列”和“坐标子序列”。
还假设节点v存储通过仅取出pi(π)的元素的第(h+1)位并且按照相同的次序将位进行级联而获得的位序列bv。换句话说,如果整数pi(π)[i]的第(h+1)位为0,则位序列bv满足bv[i]=0,并且如果第(h+1)位为1,则满足bv[i]=1。
具体地,如在图5的(a)和(b)中示出的,在本实施例中,使用相对于维度1针对坐标序列p1构建的小波树w1、和相对于维度2针对坐标序列p2构建的小波树w2。同样,图5的(a)和(b)针对每个节点示出了坐标前缀π、坐标子序列pi(π)、和与该节点对应的位序列bv。
同样,如图5的(a)示出的,小波树w1是坐标序列p1=(0,1,3,2,5,7,4,6)的小波树。将坐标序列p1的每个元素表示为三个位。将每个小波树的根节点与坐标前缀π="***"链接。因此,该坐标前缀与可以由三个位表示的所有值(即,落在["000","111"]=[0,7]范围内的所有值)对应。为此,根节点将坐标子序列p1(π)的第0+1=1位存储为位序列bv。
其次,在根节点的左侧上的子节点与前缀"0**"对应,并且与由第一位为0的三个位组成的整数对应(即,与范围[0,3]对应),并且还与通过从坐标序列p1中仅取出落入范围[0,3]内的值而获得的坐标子序列p1(π)=(0,1,3,2)对应。因此,该左子节点将第二位存储为位序列bv。注意,这同样适用于后续子节点。
小波树相对于每个内部节点v保留位序列bv的简明字典。该简明字典是支持要对长度为n的位序列b执行的三种操作(即,访问(access)、排秩(rank)、和选择(select))的数据结构。可以将这三种操作定义如下:
access(b,i)返回b上在位置i处的元素b[i];
rank1(b,i)返回存在于b[0,i)范围中的1的数量;
rank0(b,i)返回存在于b[0,i)范围中的0的数量;
select1(b,i)返回在b上出现第(i+1)个1的位置j;以及
select0(b,i)返回在b上出现第(i+1)个0的位置j。
注意,根据文献,还可以将简明字典称为简明位向量或者排秩/选择字典。
在图5的(a)和(b)中示出的示例中,为了说明起见,相对于小波树中的每个节点,示出了坐标前缀π、坐标子序列pi(π)、和比特序列bv。然而,实际上,小波树仅保留用于bv的简明字典,并且不需要保留坐标前缀π或者坐标子序列pi(π)。这是因为可以通过关于已经追溯的边缘的信息来计算坐标前缀π,并且可以通过使用针对位序列bv的简明词典来计算坐标子序列pi(π)的每个元素。因此,实际上,存储单元50仅保留简明字典作为数据结构。
换句话说,根据本实施例,构建数据结构,从而使得数据结构包括针对每个维度的子序列pi(π)的位表示,并且使得可以指定包括在子序列中、并且其中与包括在该区间中的坐标对应的点的特征值的位表示以特征值前缀开始的区间。
注意,在不同的文献中,按照各种方式来定义小波树。在上述非专利文献1中,在不使用前缀的情况下定义了小波树。然而,在本说明书中,为了说明起见,通过使用前缀来定义小波树。注意,针对这两种定义,小波树的基本结构是相同的,并且可以实现相同的操作。
而且,小波树仅需要具有允许进行树结构搜索的结构(即,具有多个节点的结构),并且不需要被明确地构成为树结构。例如,存在一种称为小波矩阵的已知方法,通过该方法,在不对每个节点的位序列进行分类的情况下实施小波树。针对本发明实施的讨论适用于按照完全相同的方式采用小波矩阵的情况。
同样,根据本实施例,在从输入接收单元30接收到查询区域输出时,搜索单元10向存储单元50发送查询并且获取数据结构51。接着,搜索单元10参考数据结构51,并且输出包括在坐标子序列中、并且其中与包括在该区间中的坐标对应的点的特征值的位表示以特征值前缀开始的区间,将其作为选定的区间,并且将与包括在该区间中的坐标对应的点的集合被全部包括在查询区域中。
同样,在聚合单元20通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息(统计量)后,将该信息输出至输出单元40。此后,输出单元40将聚合单元20已经输出的统计量输出至外部终端装置、服务器装置等。
搜索算法的概述
接下来,在描述信息处理装置100的操作之前,下面将描述信息处理装置100所使用的搜索算法的概述。
首先,考虑在z值前缀的覆盖区域c(πz)与维度r(1≤r≤d)的坐标前缀πr的覆盖区域c(πr)之间共享的区域(即,c(πz)∩c(πr))。包括在共享区域中的点是z值以z值前缀πz开始的点,并且相对于维度r的坐标以坐标前缀πr开始。注意,将在覆盖区域之间共享的区域表示为c(πz∧πr)=c(πz)∩c(πr)。
此处,包括在c(πz∧πr)中的点的集合始终与节点的坐标子序列pr(πr)中的连续区间pr(πr)[sr,er]对应,该节点与相对于维度r的小波树wr中的πr对应。这是因为已经按照z值的升序对坐标序列pr进行了存储,并且始终获得与在坐标序列pr中以πz开始的点对应的坐标作为连续区间。同样,pr(πr)是通过按照与z值的次序相同的次序从pr中取出仅以πr开始的坐标而获得的子序列,并且因此,包括在c(πz∧πr)中的点的集合始终形成连续区间。
在本实施例中,使用这种特性来执行搜索。首先,搜索单元10使用z值前缀πz作为条件来计算在与c(πz)对应的小波树的节点的坐标子序列中的区间。其次,搜索单元10通过将关于维度r的坐标前缀πr添加到该条件中,来计算在与c(πz∧πr)对应的小波树的节点的坐标子序列中的区间。
因此,将包括在查询区域中的点的集合表示为包括在与一个或者多个c(πz∧πr)对应的区间中的点集合的互斥并集。如果获得这种区间,则可以通过对区间的统计量进行求和来获取包括在查询区域中的点的统计量。
同样,在本实施例中,为了表示搜索结果所需要的信息,将以下两种类型的节点(即,节点v和节点y),定义为包含各种信息的元组。
v=(πz,<v1,[s1,e1]>,<v2,[s2,e2]>,<v3,[s3,e3]>,...,<vd,[sd,ed]>)
y=(πr,<vr,[sr,er]>)
节点v是用于搜索与c(πz)对应的区间的搜索节点。在下文中,将节点v称为“z值搜索节点”v。针对落在范围1≤k≤d内的每个维度k,当将相对于维度k与πz对应的坐标前缀k表示为πk时,节点v保留如下一对:与小波树wk上的πk对应的节点vk;和在坐标子序列pk(πk)中的区间[sk,ek]。此处,假设pk(πk)[sk,ek]是与包括在c(πz)中的点对应的区间。
节点y是保留与针对特定维度r的c(πz∧πr)对应的区间的节点。在下面的描述中,将节点y称为“选定的区间节点”。该节点y保留与小波树wr中相对于维度r的πr对应的节点vr、和与坐标子序列pr(πr)中的c(πz∧πr)对应的区间pr(πr)[sr,er]。
在根据本实施例的搜索中,首先通过使用z值搜索节点v来搜索与c(πz)对应的区间。然后,如果c(πz)满足特定条件,则将相对于维度r的前缀πr添加到该条件中,然后搜索与c(πz∧πr)对应的区间。此后,获取保留与包括在查询区域中的点对应的区间的选定的区间节点y作为搜索结果。
装置操作
接下来,将参照图6来描述根据本发明的实施例的信息处理装置100的操作。图6是示出了根据本发明的实施例的信息处理装置的操作的流程图。在下面的描述中,若适当,参照图1至图4。在本实施例中,通过操作信息处理装置100来执行信息处理方法。因此,可以用下面对信息处理装置100的操作的描述来替代对根据本实施例的信息处理方法的描述。
如在图6中示出的,首先,输入接收单元30从外部接收用于指定查询区域的范围的输入(步骤a1),并且将接收到的内容输出至搜索单元10。将该输入查询区域q表示为q=[lq1,uq1]×[lq2,uq2]×...×[lqd,uqd]。
接着,搜索单元10通过将初始值代入其中来将如上面描述的那样定义的z值搜索节点v初始化(步骤a2)。具体地,在步骤a2中,将z值搜索节点v初始化以与长度为0的z值前缀πz对应。相对于每个维度k与长度为0的z值前缀πz对应的坐标前缀πk长度也为0,并且与小波树的根节点对应。换句话说,由于该初始化,相对于每个维度k的对应节点vk用作小波树wk的根节点,并且设置为满足[sk,ek]=[0,n-1]。
接着,搜索单元10向存储单元50发送查询,并且获取数据结构51。然后,搜索单元10相对于查询区域q对数据结构51执行函数“range_search(v,q)”,并且获取一个或者多个选定的区间节点的集合{y}作为返回值(步骤a3)。同样,搜索单元10将如此获得的选定的区间节点的集合{y}输出至聚合单元20。在如此获得的{y}中包括的每个选定的区间节点y保留坐标子序列的区间,并且与该区间对应的点的集合是互斥(disjoint)的。与该区间对应的点集合的互斥并集等于包括在查询区域中的点集合的互斥并集。
接着,在从搜索单元10接收一个或者多个选定的区间节点的集合{y}时,聚合单元20调用函数“aggregate({y})”,并且获取包括在查询区域q中的点的统计量“结果”作为返回值(步骤a4)。同样,聚合单元20将如此获得的统计量输出至输出单元40。针对包括在{y}中的每个选定的区间节点y,函数“aggregate({y})”计算关于与由y保留的区间对应的点的集合的统计量,并且此后,计算统计量的总和以获取包括在查询区域中的点的统计量。
最后,输出单元40将从聚合单元20接收到的统计量输出至外部(步骤a5)。针对查询区域q的搜索处理在执行步骤a1至a5后完成。每当输入查询区域q时,便执行步骤a1至a5。
步骤a3
接下来,将参照图7至图10来更具体地描述在图6中示出的步骤a3。图7是示出了用于递归地执行正交范围搜索的函数“range_search(v,q)”的操作的流程图。通过搜索单元10向存储单元50发送查询来实现该函数。
步骤a3:概述
在详细描述在图7中示出的算法之前,将描述在图7中示出的算法的概述、和该算法所基于的概念。
函数“range_search(v,q)”是利用长度为0的z值前缀πz作为自变量来调用并且能够递归地调用自身的函数。每当函数“range_search(v,q)”递归地调用自身时,函数“range_search(v,q)”便将z值前缀πz扩展一位,并且针对已经扩展的每个πz生成对应的z值搜索节点v。将πz扩展一位相当于将覆盖区域c(πz)划分为两个区域,并且因此,覆盖区域随着πz变长而变小。
当覆盖区域c(πz)满足给定条件时,函数“range_search(v,q)”放弃递归循环,并且添加πr,并且因此进入通过使用覆盖区域c(πz∧πr)来划分空间的阶段。在覆盖区域c(πz∧πr)被完全包括在查询区域q中时,函数“range_search(v,q)”返回保留小波树的节点的坐标子序列的区间(其与覆盖区域等同)的选定的区间节点y。
此处,将更具体地描述用于进行该搜索处理所需要的z值搜索节点v=(πz,<v1,[s1,e1]>,<v2,[s2,e2]>,<v3,[s3,e3]>,...,<vd,[sd,ed]>)。此处,假设给出了z值前缀πz,并且将包括在z中并且以πz开始的连续区间表示为z[sz,ez]。如果将以πz开始的z[i]的数量表示为nz,则满足nz=ez-sz+1。该nz等于包括在覆盖区域c(πz)中的点的数量。
如上所述,针对维度1至d中的每一个,存在与πz对应的d个坐标前缀π1、π2、...、πd。在这种情况下,如果满足nz>0,则小波树w1至wd始终具有与坐标前缀对应的节点v1、v2、...、和vd。此外,存在分别与节点对应的坐标子序列p1(π1)、...、pd(πd)。
此处,如果z值在区间z[sz,ez]中以z值前缀πz开始,则意味着相对于满足1≤k≤d的k的每个pk[sz,ez]以坐标前缀πk开始。因此,可以看出,包括在区间pk[sz,ez]中的nz个连续整数也以完全相同的次序包括在pk(πk)中作为nz个连续整数。将该区间表示为pk(πk)[sk,ek]。此处,满足nz=ez-sz+1=ek-sk+1,并且满足pk(πk)[sk+i]=pk[sz+i],其中,每个i满足0≤i<nz。
包括在区间pk(πk)[sk,ek]中的坐标是z值以πz开始的坐标,并且这些点包括在覆盖区域c(πz)中。因此,相对于满足0≤i<nz的每个i,满足lπk≤pk(πk)[sk+i]≤uπk。z值搜索节点v保留z值前缀πz、和具有上述特性的区间[sk,ek]。
将参照图1、图4、和图5来描述具体示例。假设给出了长度为3的z值前缀πz="011***"。如果该z值前缀被划分为因子,则可以看出,相对于维度1长度为2的坐标前缀π1="01*"和相对于维度2长度为1的坐标前缀π2="1**"与z值前缀πz对应。在这种情况下,在以πz开始的z中的区间是z[sz,ez]=z[2,3]。满足nz=2。
此处,注意维度1。满足p1[sz,ez]={3,2}={"011","010"},并且这些值以坐标前缀π1开始。因此,按照相同的次序来将这些值包括在与在小波树w1上满足π=π1的节点v1对应的整数子序列p1(π1)中。该区间为p1(π1)[s1,e1]=p1(π1)[0,1]。
类似地,注意维度2。满足p2[sz,ez]={4,7}={"100","111"},并且这些值以坐标前缀π2开始。因此,按照相同的次序来将这些值包括在与在小波树w2上满足π=π2的节点v2对应的整数子序列p2(π2)中。该区间为p2(π2)[s2,e2]=p2(π2)[0,1]。
因此,与上述z值前缀πz对应的z值搜索节点v保留以下元素。
v=(πz,<v1,[s1,e1]>,<v2,[s2,e2]>)=("011***",<v1,[0,1]>,<v2,[0,1]>)
此外,此处定义了z值搜索节点之间的父子关系。当存在与z值前缀πz对应的z值搜索节点v时,将与πz+"0"对应的z值搜索节点定义为v的左子节点,并且将与πz+"1"对应的z值搜索节点定义为v的右子节点。例如,如果v与z值前缀"111***"对应,则v的左子节点是与z值前缀"1110**"对应的z值搜索节点,并且v的右子节点是与z值前缀"1111**"对应的z值搜索节点。
注意,在下面的描述中,将包括在z值搜索节点v中的πz的覆盖区域称为z值搜索节点v的覆盖区域。同样,在下面的描述中,在一些情况下,按照使用"."的级联格式来表示包括在z值搜索节点v中的元素。例如,将包括在z值搜索节点v中的z值前缀πz表示为v.πz。
步骤a3:具体示例
接下来,基于对上述搜索算法的概述,将描述在图7中示出的算法的细节。
如在图7中示出的,搜索单元10首先确定在z值搜索节点v的覆盖区域内是否存在点(步骤b1)。如果在步骤b1中的确定的结果为“是”,则搜索单元10进入步骤b2,并且,如果结果为“否”,则搜索单元10返回空集合。
在步骤b1中,检查相对于给定维度k包括在z值搜索节点v的覆盖区域中的点nz=ek-sk+1的数量是否大于0,并且由此执行确定。在步骤b1中,如果满足nz>0,则结果为“是”,并且如果满足nz<=0,则结果为“否”。该确定对于在不存在以πz开始的点时终止搜索是必要的。
接着,搜索单元10确定z值搜索节点v的覆盖区域是否与查询区域重叠(步骤b2)。如果在步骤b2中的确定的结果为“是”,则搜索单元10进入步骤b3,并且如果结果为“否”,则搜索单元10返回空集合。
具体地,在步骤b2中,搜索单元10通过使用πz的值来获取z值搜索节点v的覆盖区域c(πz)=[lπ1,uπ1]×[lπ2,uπ2]×,...,×[lπd,uπd]。然后,当k满足1≤k≤d时,搜索单元10针对其中一个维度k检查是否满足“uπk<lqk或者uqk<lπk”。作为检查的结果,如果上述关系为真,则搜索单元10确定结果为“否”,因为不存在空间重叠。如果上述关系不为真,则搜索单元10确定结果为“是”,因为存在空间重叠。执行步骤b2中的确定以执行修剪,从而防止进一步搜索不与查询区域重叠的覆盖区域。
接着,搜索单元10将z值搜索节点v的覆盖区域与查询区域相比较以计算包括维度数h(步骤b3)。根据该定义,可以通过对满足lqk≤lπk并且uπk≤uqk的维度k的数量进行计数来计算包括维度数h。
接着,搜索单元10确定包括维度数h是否小于d-1(步骤b4)。如果在步骤b4中的确定的结果为“是”,则搜索单元10进入步骤b5,并且如果结果为“否”,则搜索单元10返回步骤b6中的“range_search_1d(v,q)”。该函数“range_search_1d(v,q)”是通过针对特定维度r使用c(πz∧πr)来划分空间并且返回选定的区间节点的集合{y}的函数。
接着,搜索单元10将z值搜索节点v的左子节点代入vleft,并且将z值搜索节点v的右子节点代入vright(步骤b5)。具体地,在步骤b5中,通过使用关于z值搜索节点v的信息,搜索单元10计算v的左子节点(即,与πz+"0"对应的搜索节点)和v的右子节点(即,与πz+"1"对应的搜索节点)。注意,稍后将参照图8描述步骤b5。通过执行在图8中示出的算法来执行步骤b5。
此后,在步骤b5中,搜索单元10计算z值搜索节点v的右子节点和左子节点,并且按照以下方式来递归地调用相同的函数。
返回range_search(vleft,q)∪range_search(vright,q)
通过递归地调用该函数,搜索单元10可以对覆盖区域已经被减半的前缀πz重复地执行相同的计算。
步骤b5:概述
接下来,将参考图8具体描述在步骤b5中执行的处理。图8是示出用于计算z值搜索节点v的左子节点和右子节点的函数“get_children(v)”的操作的流程图。还通过搜索单元10向存储单元50发送查询来实现函数“get_children(v)”。
首先,在详细描述在图8中示出的算法之前,将描述如何通过z值搜索节点v来计算左节点和右节点。
首先,将通过将位b添加至z值搜索节点v与其对应的z值前缀πz的末尾处而获得的新z值表示为π'z,并且对计算与π'z对应的新z值搜索节点v'进行了思考。如果b为0,则z值搜索节点v'为z值搜索节点v的左子节点,并且,如果b为1,则z值搜索节点v'为z值搜索节点v的右子节点。在下面的描述中,满足v'=(π'z,<v'1,[s'1,e'1]>,<v'2,[s'2,e'2]>,<v'3,[s'3,e'3]>,...,<v'd,[s'd,e'd]>)。
如果满足维度g=length(πz)modd+1,则针对维度g,以下表达式成立。注意,在上面的描述中的length()表示前缀的长度。
π'k=πk+b(在k=g的情况下)
π'k=πk(在其它情况下)
换句话说,当通过与πz对应的z值搜索节点v来计算与π'z对应的z值搜索节点v'时,相对于维度k(≠g)与π'z对应的坐标前缀π'k等于与πz对应的坐标前缀πk。然而,相对于维度g与π'z对应的的坐标前缀π'g是与πz对应并且已经添加了位b的坐标前缀π'g。由于满足π'g=πg+b,因此,与小波树wg上的π'g对应的节点v'g是与πg对应的节点vg的子节点。
具体地,如在图1、图4、和图5中示出的,坐标前缀π1="01*"和π2="1**"与z值前缀πz="011***"对应。在这种情况下,如果满足b=1(即,如果假设π'z=πz+”1”=“0111**”),则π'z="0111**",与π'1="01*"和π'2="11*"对应。同样,满足g=length(πz)modd+1=3mod2+1=2。
通过上面的结果,可以看出,对π'1=π1和π'2=π2+b进行了分层,并且实际上相对于维度g=2添加了位b。由于满足b=1,因此,与π'g对应的节点v'g是与πg对应的节点vg的右子节点。
此处,注意相对于维度g的小波树wg,其是坐标前缀发生改变的唯一维度。由于已经知道与πz对应的区间pg(πg)[sg,eg],因此,基于该区间对计算与π'z=πz+b对应的区间pg(π'g)[s'g,e'g]进行了思考。
注意由与小波树wg上的πg对应的节点vg保留的位序列bvg。通过取出pg(πg)[sg,eg]的第(length(πg)+1)位并且对该位进行级联而获得位序列bvg[sg,eg]。在pg(πg)[sg,eg]中的坐标与具有与在z[sz,ez]中的z值相同次序的相同点对应。因此,位序列bvg[sg,eg]等于通过取出z[sz,ez]的第(length(πz)+1)位并且对该位进行级联而获得的序列。已经按照升序对z值进行了分类,并且每个z[sz,ez]以πz开始。因此,确保可以将通过取出第(length(πz)+1)位并且对该位进行级联而获得的位序列(诸如,"000…000111…111")分为前半序列(在该前半序列中,仅连续地排列有0)和后半序列(在该后半序列中,仅连续地排列有1)。
分别将出现在位序列bvg[sg,eg]中的0的数量和1的数量表示为nz0和nz1。同样,满足nz=nz0+nz1。如上面考虑的,在位序列bvg[sg,eg+nz0-1]中的所有位都为0。在bvg[sg+nz0,eg]中的所有位都为1。这意味着区间z[sz,sz+nz0-1]以πz+"0"开始,并且区间z[sz+nz0,ez]以πz+"1"开始。因此,如果满足π'z=πz+"0",则可以将[s'z,e'z]计算为[s'z,e'z]=[sz,sz+nz0-1],并且,如果满足π'z=πz+"1",则可以将[s'z,e'z]计算为[s'z,e'z]=[sz+nz0,e'z]。可以通过使用位序列bvg的简明字典来将nz0计算为nz0=rank0(bvg,eg+1)-rank0(bvg,sg)。可以将nz1计算为nz1=nz-nz0。
如果满足b=0,则与π'g对应的节点v'g是与πg对应的节点vg的左子节点。此外,可以如下面那样来计算与pg(π'g)上的π'z对应的区间[s'g,e'g]。即,满足s'g=rank0(bvg,sg)和e'g=s'g+nz0-1。这是因为如下事实:与给定i对应的bvg[i]的位为0意味着对应的整数pg(πg)[i]以π'g=πg+"0"开始,并且仅从pg(πg)中取出与位0对应的这种整数并且将其包括在pg(π'g)中。
类似地,如果满足b=1,则节点v'g是在节点vg的右子节点,并且还可以按照与b=0的情况相同的方式来计算在节点v'g上的对应区间。同样,满足s'g=rank1(bvg,sg)和e'g=s'g+nz1-1。如上所述,可以获取与pg(π'g)中的π'z对应的区间pg(π'g)[s'g,e'g],该pg(π'g)与相对于维度g的坐标前缀π'g对应。
下面检查满足k≠g的其它维度的情况。相对于这些维度k,满足π'k=πk。因此,在相同的坐标子序列pk(π'k)=pk(πk)上获得与π'z对应的范围。此处,已知与以πz开始的区间z[sz,ez]对应的区间是[sk,ek]。因此,可以通过将该区间划分为前半区间和后半区间,并且如果满足π'z=πz+"0"则执行更新以满足[s'k,e'k]=[sk,sk+nz0-1]和如果满足π'z=πz+"1"则执行更新以满足[s'k,e'k]=[sk+nz0,ek],来获取与π'z对应的区间。
基于上面的描述,已经发现,当给出与πz对应的z值搜索节点v时,还可以计算在与已经向其添加了一位的π'z对应的z值搜索节点v'中包括的信息。即,可以计算与πz+"0"对应的左子节点vleft和与πz+"1"对应的右子节点vright。
具体地,假设已知πz="011***"、π1="01*"、π2="1**"、z[sz,ez]=z[2,3]、p1(π1)[s1,e1]=p1(π1)[0,1]、以及p2(π2)[s2,e2]=p2(π2)[0,1]作为事实。还假设满足b=1。在这种情况下,可以按照以下方式来获取与π'z=πz+"1"="0111**"对应的区间。
即,由于满足π'1=π1="01*"并且π'2=π2+"1"="11*",因此,坐标前缀发生改变的唯一维度是维度g=2。因此,对维度g=2的小波树加以关注,并且对通过p2(π2)[s2,e2]来计算p2(π'2)[s'2,e'2]进行了思考。
由于由节点v2保留的位序列是bv2="0101",因此,满足bv2[s2,e2]=bv2[0,1]="01",并且满足nz0=1和nz1=1。由于bv2[0,1]与区间z[2,3]中的第四位对应,因此,可以看出,z[2]的第四位为0并且z[3]的第四位为1。因此,由于b=1,所以v'2是v2的右子节点,并且满足s'2=rank1(bv2,s2)=0和e'2=s'2+nz1-1=0+1-1=0。
类似地,相对于维度1,将长度为2的区域划分为长度为1的多个区域,并且因此,按照以下方式来计算新的区间。
[s'1,e'1]=[s1+nz0,e1]=[0+1,1]=[1,1]
基于上面的描述,可以计算相对于π'z的以下值。
π'z="0111**"、π'1="01*"、π'2="11*"、z[s'z,e'z]=z[3,3]、p1(π'1)[s'1,e'1]=p1(π'1)[1,1]、p2(π'2)[s'2,e'2]=p2(π'2)[0,0]
步骤b5:具体示例
在图8中示出了以算法的形式表示的上述检查。下面将详细描述在图8中示出的算法。根据在图8中示出的算法,如下执行用于计算z值搜索节点v的左子节点和右子节点的处理。vleft指表示z值搜索节点v的左子节点的元组,vright指表示z值搜索节点v的右子节点的元组。
首先,如在图8中示出的,搜索单元10将z值搜索节点v的内容复制到vleft,并且将z值搜索节点v的内容复制到vright(步骤c1)。因此,包括在vleft和vright两者中的小波树的节点vk都与包括在z值搜索节点v中的小波树的节点vk相同。
其次,相对于分别包括在vleft和vright中的πk和vk,更新与z值搜索节点v的差(步骤c2)。换句话说,假设g=length(πz)modd+1,并且将vleft.πz=v.πz+"0"代入vleft.πz,并且将vright.πz=v.πz+"1"代入vright.πz。此外,将v.vg的左子节点代入vleft.vg,并且将v.vg的右子节点代入vright.vg。同样,满足nz=eg-sg+1。通过使用位序列bvg的简明字典,从表达式nz0=rank0(bvg,eg+1)-rank0(bvg,sg)导出nz0。使用nz1=nz-nz0计算nz1。
接着,搜索单元10进入相对于维度k的循环以计算区间[sk,ek](步骤c3)。接着,搜索单元10确定在循环期间是否满足k=g(步骤c4)。然后,如果在步骤c4中的确定结果为“是”,则搜索单元10进入步骤c5,并且如果结果为“否”,则搜索单元10进入步骤c6。
如果在步骤c4中的确定结果为“是”(即,如果满足k=g),则搜索单元10针对维度g执行计算(步骤c5)。在步骤c5中,满足vleft.sg=rank0(bvg,sg)和vleft.eg=vleft.sg+nz0-1。而且,满足vright.sg=rank1(bvg,sg)和vright.eg=vright.sg+nz1-1。
另一方面,如果在步骤c4中的确定结果为“否”(即,如果不满足k=g),则搜索单元10针对除了维度g之外的k执行计算(步骤c6)。在步骤c6中,满足vleft.sk=v.sk和vleft.ek=v.sk+nz0-1。同样,满足vright.sk=v.sk+nz0和vright.ek=v.ek。
在完成相对于维度k的循环时(步骤c7),返回vleft和vright并且步骤b5完成。按照这种方式,在图8中示出的算法计算z值搜索节点v的左节点和右节点。
这结束了对当步骤b4的结果为“是”时根据在图7中示出的算法的操作的描述。接下来,将描述当步骤b4的结果为“否”时的操作。换句话说,将描述在图7中示出的函数“range_search_1d(v,q)”的操作。
步骤b6:概述
接下来,将参照图9和图10来描述在图7中示出的步骤b6。函数“range_search_1d(v,q)”是向其输入z值搜索节点v和查询区域q、并且返回保留与包括在查询区域q中的覆盖区域c(πz∧πr)对应的区间的选定的区间节点y的函数。
在详细描述在图9和图10中示出的算法之前,下面将描述操作的概述。
将考虑在图7中示出的步骤b4的结果为“否”的情况(即,当前缀πz的覆盖区域c(πz)的包括维度数已经达到d-1时)。包括维度数已经达到d-1的事实意味着已经相对于d-1个维度满足了包括条件。在这种情况下,将未包括进来的剩余的一个维度表示为维度r。考虑相对于维度r与πz对应的坐标前缀πr,并且注意与πz对应的区间pr(πr)[sr,er]。如上所述,该区间按照相同的次序包括与在pr[sz,ez]中的坐标相同的坐标。
将被包括在p[sz,ez]中的所有点包括在πz的覆盖区域中,并且因此,满足相对于除了维度r之外的所有维度的包括条件,但是不满足相对于维度r的包括条件。换句话说,尚未满足相对于维度r的坐标的值pr被包括在[lqr,uqr]中的条件。
因此,根据在图9和图10中示出的算法,仅扩展了πz以减小覆盖区域,从而形成被包括在查询区域中的覆盖区域。换句话说,返回保留在与得到的覆盖区域的坐标子序列中的区间的选定的区间节点,直到获得相对于维度r被包括在[lqr,uqr]中的覆盖区域c(πz∧π'r)为止,其中,π'r表示通过扩展πr而获得的坐标前缀。
步骤b6:具体示例
接下来,将描述在图7中示出的步骤b6的具体例。图9是示出了在图7中示出的函数“range_search_1d(v,q)”的操作的示意图。如在图9中示出的,搜索单元10调用函数“range_search_1d(v,q)”,并且计算维度r(步骤d1),z值搜索节点v的覆盖区域关于该维度r不被包括在查询区域q中。
接着,搜索单元10相对于维度r计算与πz对应的前缀πr(步骤d2)。然后,搜索单元10通过使用在步骤d2中获得的值来如下面那样调用递归函数,并且执行在图10中示出的每个步骤。
returnrange_search_1d_rec(πr,v.vr,v.sr,v.er,q.lqr,q.uqr)
此处,在参照图6进行详细描述之前,将描述函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”的概述。函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”是返回在其z值以πz开始并且相对于维度r的坐标的值pr被包括在[lqr,uqr]中的坐标子序列pr(πr)中的区间pr(π'r)[s'r,e'r]的递归函数。换句话说,该函数是返回与完全被包括在查询区域q中的覆盖区域c(πz∧π'r)对应的区间的函数。注意,π'r表示通过扩展前缀πr而获得的坐标前缀。
通过在每个节点上计算在区间的左端处的s'r和在区间的右端处的e'r来实现由函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”执行的操作。首先,考虑在与前缀πr对应的节点vr的坐标子序列中的区间pr(πr)[sr,er]。
然而,假设该区间是与其z值以πz开始的点对应的区间。在这种情况下,考虑搜索节点vr的小波树的左子节点vleft和右子节点vright。假设pr(π'r)[sr,er]表示与由以π'r开始并且从区间pr(πr)[sr,er]中取出的整数组成的子序列对应的区间,其中,π'r表示与子节点对应的前缀。
根据小波树的定义,在移动至左子节点时,可以通过使用表达式s'r=rank0(bvr,sr)和e'r=rank0(bvr,er+1)-1来获取区间[s'r,e'r]。另一方面,在移动至右子节点时,可以通过使用表达式s'r=rank1(bvr,sr)和e'r=rank1(bvr,er+1)-1来获取区间[s'r,e'r]。
针对每个节点重复执行上述操作,并且当与节点对应并且以前缀π'r开始的坐标的所有值都包括在[lqr,uqr]中时,返回在节点中包括区间pr(π'r)[s'r,e'r]的选定的区间节点y。只有落在[lqr,uqr]范围内的坐标出现在该区间中,并且因此,该区间与满足相对于维度r的范围条件的点对应。换句话说,选定的区间节点y与完全包括在查询区域中的点对应。上述操作的时间复杂度等于相对于小波树已经知道的二维“范围计数”的时间复杂度,并且为o(logn)。
接下来,将参照图10来详细描述函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”的操作。图10是示出了在图9中示出的函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”的操作的示意图。
如在图10中示出的,搜索单元10执行函数“range_search_1d_rec(πr,vr,sr,er,lqr,uqr)”,并且确定是否满足sr>er或者
接着,搜索单元10确定是否满足
如果在步骤e2中的确定结果为“是”(即,如果满足
另一方面,如果在步骤e2中的确定结果为“否”,则搜索单元10通过使用关于在图10中示出的“rank”的四个表达式来计算左子节点的区间[sleft,eleft]和右子节点的区间[sright,eright],其中,bvr表示与πr对应的节点vr的位序列(步骤e4)。
此后,为了对右子节点和左子节点执行相同的处理,搜索单元10递归地调用以下函数。
returnrange_search_1d_rec(πr+"0",vleft,sleft,eleft,lqr,uqr)∪range_search_1d_rec(πr+"1",vright,sright,eright,lqr,uqr)
步骤a4
接下来,将描述在图6中示出的步骤a4中调用的函数“aggregate({y})”。该功能由聚合单元20来执行。
通过使用函数“aggregate({y})”,聚合单元20可以相对于在{y}中包括的每个选定的区间节点y,计算关于与选定的区间节点y对应的点的集合的统计量。此后,通过使用该统计量,聚合单元20可以计算关于包括在查询区域q中的点的统计量。
函数“aggregate({y})”是各种聚合函数的抽象,并且可以使用信息处理装置100来通过用特定聚合函数替换该函数执行各种类型的正交范围搜索。
例如,可以使用信息处理装置100来对包括在查询区域q中的点的数量进行计数。具体地,如果选定的区间节点y=(πr,<vr,[sr,er]>)被包括在输入{y}中,则在坐标子序列中的区间pr(πr)[sr,er]与包括在查询区域q中的点对应。这意味着包括在该区间中的(er-sr+1)个点包括在查询区域q中。换句话说,可以通过计算所有获得的选定的区间节点y的(er-sr+1)的总和来计算包括在查询区域中的点的数量。如果是这种情况,则聚合单元20输出包括在查询区域q中的点的数量作为统计量。
而且,如果所有的点p都赋有权重w(p),则信息处理装置100可以计算在查询区域中包括的点的权重的总和。如果已经准备好允许计算在序列中的区间的总权重的数据结构,则可以在通过按照已经针对在每个坐标子序列pr(πr)中的每个坐标设定了通过以相同次序排列对应点p的权重w(p)而获得的序列wr(πr)的情况下实现上述操作。
这种数据结构的示例是处理“部分和”的现有数据结构。在这种数据结构的情况下,如果已知在坐标子序列中的区间pr(πr)[sr,er]与包括在查询区域中的点对应,则可以通过计算在与区间[sr,er]对应的权重的序列中的每个区间wr(πr)[sr,er]中的总权重来计算包括在查询区域q中的所有点的权重的总和,并且可以对总权重进行求和。如果是这种情况,则聚合单元20输出包括在查询区域q中的所有点的总权重作为统计量。
类似地,信息处理装置100可以用作返回包括在查询区域q中的每个点的列表的报告查询。换句话说,针对坐标子序列中的区间pr(πr)[sr,er],可以通过回溯小波树来指定包括在该区间中的元素pr(πr)[j]在原始整数序列pr中的位置i。在这种情况下,点p[i]包括在查询区域中。如果是这种情况,则聚合单元20输出包括在查询区域q中的每个点的列表作为统计量。
如上所述,根据本实施例,可以实现各种类型的正交范围搜索。同样,本实施例不限于在图6至图10中示出的独立使用的算法的模式,并且可以是其中(在适当的时候)将其它搜索算法与在图6至图10中示出的算法结合的模式。
例如,在本实施例中,可以将简单的扫描处理与在图1至图10中示出的算法相结合。根据在图6至图10中示出的算法,通过使用z值搜索节点v划分在由z值组成的序列z中的范围z[sz,ez]执行搜索。然而,与回溯小波树结构相比较,如果范围z[sz,ez]变窄,则可以通过扫描与坐标序列pk对应的范围pk[sz,ez]并且相对于每个值pk[i]检查是否满足条件来实现更快的速度。为此,如上面描述的那样结合扫描处理。如果是这种情况,则虽然需要保留坐标序列pk,但是总数据结构也具有线性大小。
实施例的效果
本实施例具有时间复杂度低于k-d树的效果。为了表明该事实,将对最差时间复杂度进行分析。通常的k-d树是通过该方法执行划分直到包括维度数达到d的方法,而本实施例是通过该方法执行划分直到包括维度数达到d-1的方法。下文描述了该事实对最差时间复杂度的影响。
首先,与根据k-d树和本实施例的方法相似,当树结构平衡时,相对于在针对每个深度交替地切换维度的同时通过将空间划分为两个空间而进行的搜索,估计节点的划分数量。当空间划分的数量处于最大值时,时间复杂度最差。换句话说,当通过执行一次划分而产生的两个覆盖区域始终与查询区域重叠时,时间复杂度最差。
图11示出了在最差的情况下的搜索节点的数量与包括维度数之间的关系。图11是示出了在二维情况下的搜索节点的数量变化和包括维度数量变化的示意图。如在图11中示出的,树结构中的一个节点与一个搜索节点对应。当树结构中的深度增加1时,节点被划分一次,成为两个搜索节点。节点上的数字示出了包括维度数。可以看出,包括维度数高的节点的数量随着划分的执行而增加。
此处,将执行d次的划分视为一个集合。将考虑在th(m)与th(m-1)之间为真的递归公式,其中,th(m)表示包括维度数在深度m*d处为h的节点的数量。如果执行d次划分,则将一个覆盖区域划分为2d个覆盖区域。在这点上,始终相对于每个维度划分覆盖区域一次。即使相对于已经包括的维度执行划分,包括维度数也不增加。因此,为了计算在深度m*d处包括维度数为h的节点的数量,考虑相对于在(m-1)*d处包括维度数为i(≤h)的节点的新包括的h-i维度的数量。
该递归公式如下面的数学式1所示。注意,在下面的数学式1中的c(x,y)表示组合的数量。
数学式1
通过上面的数学式1可以看出,当执行d次划分时,节点的总数增加了2d倍,并且在这些节点中,包括维度数为h的节点的数量增加了2h倍。
由于重复了这种划分log(n)/d次,搜索树整体变为深度为logn的二叉树,并且节点的总数达到o(n),并且划分完成。在这些节点中,包括维度数为h的节点的数量为o(n(h/d))。注意,包括维度数为0的节点的数量为o(logn)。
因此,可以做出如下说明。首先,如果搜索完全根本未终止,则划分的次数最多为o(n)次。如果划分在包括维度数达到d时终止,则划分的次数为o(n(d-1)/d)。如果划分在包括维度数达到d-1时终止,则划分的次数为o(n(d-2)/d)。根据k-d树,划分在包括维度数达到d时终止,并且因此,时间复杂度为o(n(d-1)/d)。这与常规已知的阶数相匹配。
可以将对k-d树的这种分析应用于本实施例。这是因为在根据本实施例的搜索中的z值搜索节点相对于每个维度交替地划分空间,并且可以通过使用与用于k-d树的方法相同的方法来估计时间复杂度。然而,需要进行少量修改以适合本实施例。
根据本实施例,划分在包括维度数达到d-1时终止,并且因此,划分的次数或者z值搜索节点的数量最大为o(n(d-2)/d)。然而,z值的长度为dlogn,并且z值搜索节点可以包括仅具有一个子节点的节点。因此,在最坏的情况下,可以对通过划分生成的每个z值搜索节点执行dlogn次不必要的计算。当d为常数时,时间复杂度为o(logn)。
同样,相对于每个z值搜索节点的range_search_1d的时间复杂度为o(logn)。因此,在根据本实施例的方法中,相对于o(n(d-2)/d)个z值搜索节点中的每一个的时间复杂度为o(logn)+o(logn),并且总时间复杂度为o(n(d-2)/dlogn)。
然而,满足d=2的情况是特殊情况。搜索循环在包括d-1=1维时终止,并且因此,进行了划分的节点的数量与包括维度数为0的节点的数量o(logn)成比例,该o(logn)为其包括维度数为0的节点的数量。每个节点的时间复杂度为o(logn),并且因此,当d=2时,总时间复杂度为o(log2n)。
上面的描述是用于输出包括在查询区域中的点的数量的计数查询的情况。在用于输出每个包括的点的列表的报告查询的情况下,要输出的每个f点的计算时间为o(logn)。图12是总结。如在图12中示出的,与使用k-d树执行的搜索处理相比较,本发明改进了时间复杂度的阶次,并且此外,与常规的小波树不同,本发明可应用于维度的数量为三个或者更多个的情况。图12是示出了本发明与传统方案之间针对时间复杂度的比较的示意图。
程序
根据本发明的实施例的程序可以是使计算机执行在图6中示出的步骤a1至a5的程序。可以通过将该程序安装到计算机并且执行程序来实现根据本实施例的信息处理装置和信息处理方法。如果是这种情况,则计算机的cpu(中央处理单元)起到搜索单元10、聚合单元20、输入接收单元30、和输出单元40的作用,并且执行处理。同样,在本实施例中,通过将构成这些单元的数据文件存储在为计算机提供的存储装置(诸如,硬盘)中来实现存储单元50。
注意,根据本实施例的程序可以由构建为包括多个计算机的计算机系统来执行。例如,如果是这种情况,则多个计算机可以分别起到搜索单元10、聚合单元20、输入接收单元30、和输出单元40的作用。同样,可以在与执行根据本实施例的程序的计算机不同的计算机中构建存储单元50。
此处,将参照图13来描述通过执行根据本实施例的程序来实现信息处理装置100的计算机。图13是示出了根据本发明的实施例的实现信息处理装置的计算机的示例的框图。
如在图13中示出的,计算机110包括cpu111、主存储器112、存储装置113、输入接口114、显示控制器115、数据读取器/写入器116、和通信接口117。经由总线121来使这些单元彼此连接,从而使得可以在其间执行数据通信。
cpu111将存储在存储装置113中的根据本实施例的程序(代码)加载到主存储器112,并且按照预定次序来执行程序以执行各种计算。通常,主存储器112是易失性存储装置,诸如,dram(动态随机存取存储器)。根据本实施例的程序提供为处于存储在计算机可读存储介质120中的状态。可以通过经由通信接口117连接的互联网来分布根据本实施例的程序。
除了硬盘驱动器之外,存储装置113的具体示例包括,半导体存储装置,诸如,闪速存储器。输入接口114协调cpu111与输入装置118(诸如,键盘或者鼠标)之间的数据传输。显示控制器115连接至显示装置119,并且控制在显示装置119上的显示。
数据读取器/写入器116协调cpu111与存储介质120之间的数据传输,从存储介质120读取程序,并且将由计算机110进行的处理的结果写入存储介质120。通信接口117协调cpu111与其它计算机之间的数据传输。
存储介质120的具体示例包括:通用半导体存储装置(诸如,cf(compactflash(紧凑型闪存)(tm))、sd(安全数字)、磁存储介质(诸如,柔性盘)、和光存储介质(诸如,cd-rom(光盘只读存储器))。
虽然一部分或者全部上述实施例可以由下面描述的补充说明1至21来表示,但是本发明不限于该描述。
补充说明1
一种处理表示在多维度空间中包括的点的集合的数据结构的信息处理装置,该信息处理装置包括:
搜索单元,当将特定多维度区域指定为查询区域时,该搜索单元在构建数据结构的多维度区域内指定被表示为在以特征值前缀开始的区域与相对于相应维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域,并且输出作为在与指定区域对应的数据结构中包括的区间的选定的区间,特征值前缀是从点的特征值的位表示获得的前缀,并且坐标前缀是相对于特定维度从点的坐标的位表示获得的前缀;以及
聚合单元,该聚合单元通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
补充说明2
根据补充说明1的信息处理装置,
其中,构建数据结构,从而使得通过使用子序列的位表示的一部分来表示数据结构,子序列是相对于每个维度在保持次序的同时使用坐标序列从相对于维度的坐标序列中仅提取其位表示以相同的坐标前缀开始的坐标来获得,并且从而使得可以指定包括在子序列中、并且满足以下条件的区间:与包括在区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件;通过相对于每个维度按照与特征值相同的次序从特征值序列中取出相对于所述维度的点的坐标来获得所述坐标序列,并且通过按照升序来排列在所述多维度空间中的所述点的集合的特征值来获得所述特征值序列,以及
搜索单元输出包括在子序列中并且满足以下条件的区间作为选定的区间:与包括在所述区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件;以及与包括在所述区间中的坐标对应的点的集合被全部包括在所述查询区域中的条件。
补充说明3
根据补充说明2的信息处理装置,
其中,所述搜索单元针对在所述子序列中包括的、并且满足与包括在所述区间中的坐标对应的点的特征值的位表示以特征值前缀开始的条件的所述区间,确定所述区间是否满足以下条件:与包括在所述区间中的坐标对应的点的集合完全包括在查询区域中的条件,以及
如果确定所述区间不是完全包括在查询区域中的区间,则通过扩展用于提取已经经过所述确定的子序列的坐标前缀来设置第二坐标前缀,以及
输出在通过使用所述第二前缀提取坐标而获得的第二子序列中包括的、并且满足以下条件的区间作为选定的区间:与包括在第二子序列中的所述区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件;以及与包括在第二子序列中的所述区间中的坐标对应的点的集合被全部包括在查询区域中的条件。
补充说明4
根据补充说明1的信息处理装置,
其中,所述点的特征值是基于通过交替地组合在相应维度中的点的坐标的位表示而获得的位表示的值。
补充说明5
根据补充说明2的信息处理装置,
其中,构建数据结构,从而使得:数据结构具有多个节点;通过使用位的序列来表示多个节点中的每一个节点,位的序列是从与所述子序列对应的坐标的位表示的特定数位取出的、并且按照与所述子序列相同的次序排列的;以及数据结构允许指定包括在所述子序列中、并且满足以下条件的区间:与包括在区间中的坐标对应的点的特征值的位表示以特征值前缀开始的条件。
补充说明6
根据补充说明1的信息处理装置,
其中,聚合单元计算选定的区间的长度和的值作为所述信息,并且输出这样计算出的值。
补充说明7
根据补充说明1的信息处理装置,
其中,聚合单元相对于每个维度计算包括在选定的区间中的所有坐标作为所述信息,并且输出这样计算出的所有坐标。
补充说明8
一种用于处理表示在多维度空间中包括的点的集合的数据结构的信息处理方法,该信息处理方法包括:
(a)步骤:当将特定多维度区域指定为查询区域时,在构建数据结构的多维度区域内指定表示为在以特征值前缀开始的区域与分别相对于维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域,特征值前缀是从点的特征值的位表示获得的前缀,并且坐标前缀是相对于特定维度从点的坐标的位表示获得的前缀;
(b)步骤:输出作为包括在与在步骤(a)中指定的区域对应的数据结构中的区间的选定的区间;以及
(c)步骤:通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
补充说明9
根据补充说明8的信息处理方法,
其中,构建数据结构,从而使得通过使用子序列的位表示的一部分来表示数据结构,子序列是相对于每个维度在保持次序的同时通过使用坐标序列从相对于维度的坐标序列中仅提取其位表示以相同的坐标前缀开始的坐标来获得,并且从而使得可以指定包括在子序列中并且满足与包括在区间中的坐标对应的点的特征值的位表示以特征值前缀开始的条件的区间,通过相对于每个维度从特征值序列中按照特征值与相同的次序取出相对于该维度的点的坐标来获得所述坐标序列,并且通过按照升序来排列在所述多维度空间中的点的集合的特征值来获得所述所述特征值序列,以及
在步骤(a)中,输出包括在子序列中并且满足以下条件的区间,作为选定的区间:与包括在区间中的坐标对应的点的特征值的位表示以特征值前缀开始的条件;以及与包括在区间中的坐标对应的点的集合被全部包括在查询区域中的条件。
补充说明10
根据补充说明9的信息处理方法,
其中,在步骤(a)中,针对包括在子序列中、并且满足与包括在区间中的坐标对应的点的特征值的位表示以特征值前缀开始的条件的区间,确定所述区间是否满足以下条件:与包括在区间中的坐标对应的点的集合完全包括在查询区域中,以及
如果确定所述区间不是完全包括在查询区域中的区间,则通过扩展用于提取已经经过确定的子序列的坐标前缀来设置第二坐标前缀,以及
输出包括在通过使用所述第二前缀提取坐标而获得的第二子序列中的、并且满足以下条件的区间作为选定的区间:与包括在第二子序列中的区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件;以及与包括在第二子序列中的区间中的坐标对应的点的集合被全部包括在查询区域中的条件。
补充说明11
根据补充说明8的信息处理方法,
其中,点的特征值是基于位表示的值,该位表示是通过交替地组合在相应维度中的点的坐标的位表示而获得的。
补充说明12
根据补充说明9的信息处理方法,
其中,构建数据结构,从而使得:数据结构具有多个节点;通过使用位的序列来表示多个节点中的每一个节点,所述位的序列是从与子序列对应的坐标的位表示的特定数位取出的并且按照与所述子序列相同的次序排列的;以及数据结构允许指定包括在子序列中并且满足以下条件的区间:与包括在区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始。
补充说明13
根据补充说明8的信息处理方法,
其中,在步骤(c)中,计算选定的区间的长度和的值作为所述信息,并且输出这样计算出的值。
补充说明14
根据补充说明8的信息处理方法,
其中,在步骤(c)中,相对于每个维度计算包括在选定的区间中的所有坐标作为所述信息,并且输出这样计算出的所有坐标。
补充说明15
一种计算机可读存储介质,该计算机可读存储介质存储用于使计算机执行信息处理以处理表示在多维度空间中包括的点的集合的数据结构的程序,该程序使计算机执行:
(a)步骤:当将特定多维度区域指定为查询区域时,在构建数据结构的多维度区域内指定表示为在以特征值前缀开始的区域与分别相对于维度以坐标前缀开始的区域之间共享的部分、并且包括在查询区域中的区域,特征值前缀是从点的特征值的位表示获得的前缀,并且坐标前缀是相对于特定维度从点的坐标的位表示获得的前缀;
(b)步骤:输出作为包括在与在步骤(a)中指定的区域对应的数据结构中的区间的选定的区间;以及
(c)步骤:通过使用选定的区间来计算关于包括在查询区域中的点的集合的信息。
补充说明16
根据补充说明15的计算机可读存储介质,
其中,构建所述数据结构,从而使得通过使用子序列的位表示的一部分来表示数据结构,所述子序列是相对于每个维度在保持次序的同时通过使用坐标序列从相对于维度的坐标序列中仅提取其位表示以相同的坐标前缀开始的坐标来获得的,并且从而使得可以指定包括在子序列中、并且满足包括在区间中的坐标对应的点的特征值的位表示以特征值前缀开始的条件的区间,通过相对于每个维度从特征值序列中取出相对于维度在与特征值相同的次序中的点的坐标来获得所述坐标序列,并且通过按照升序排列在所述多维度空间中的点的集合的特征值来获得所述特征值序列,以及
在步骤(a)中,输出包括在子序列中并且满足以下条件的区间,作为选定的区间:与包括在区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件;以及与包括在区间中的坐标对应的点的集合被全部包括在查询区域中的条件。
补充说明17
根据补充说明16的计算机可读存储介质,
其中,在步骤(a)中,针对包括在子序列中并且满足与包括在区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件的区间,确定所述区间是否满足以下条件:与包括在所述区间中的坐标对应的点的集合完全包括在查询区域中,以及
如果确定所述区间不是完全包括在查询区域中的区间,则通过扩展用于提取已经经过确定的子序列的坐标前缀来设置第二坐标前缀,以及
输出包括在通过使用第二前缀提取坐标而获得的第二子序列中、并且满足以下条件的区间,作为选定的区间:与包括在第二子序列中的区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始的条件;以及与包括在第二子序列中的区间中的坐标对应的点的集合被全部包括在查询区域中的条件。
补充说明18
根据补充说明15的计算机可读存储介质,
其中,所述点的特征值是基于通过交替地组合在相应维度中的点的坐标的位表示而获得的位表示的值。
补充说明19
根据补充说明16的计算机可读存储介质,
其中,构建所述数据结构,从而使得:所述数据结构具有多个节点;通过使用位的序列来表示多个节点中的每一个节点,位的序列是从与子序列对应的坐标的位表示的特定数位取出的并且按照与子序列相同的次序排列的;以及所述数据结构允许指定包括在子序列中并且满足以下条件的区间:与包括在所述区间中的坐标对应的点的特征值的位表示以所述特征值前缀开始。
补充说明20
根据补充说明15的计算机可读存储介质,
其中,在步骤(c)中,计算选定的区间的长度和的值作为所述信息,并且输出这样计算出的值。
补充说明21
根据补充说明15的计算机可读存储介质,
其中,在步骤(c)中,相对于每个维度计算包括在选定的区间中的所有坐标作为所述信息,并且输出这样计算出的所有坐标。
尽管上面参照实施例描述了本发明,但是本发明不限于该实施例。本领域的技术人员压要了解,在本发明的范围内,可以对本发明的构成和细节进行各种修改。
本申请基于并且要求2014年9月19日提交的日本专利申请第2004-191102号的优先权,其公开内容通过引用的方式全部并入本文。
工业实用性
如上所述,根据本发明,可以通过使用具有线性大小的数据结构来以与k-d树的情况相比较更快的速度实现相对于期望维度的正交范围搜索。在其中需要从大量数据集中搜索需要的数据的各种领域中,本发明是有用的。
附图标记的描述
10:搜索单元
20:聚合单元
30:输入接收单元
40:输出单元
50:存储单元
51:数据结构
100:信息处理装置
110:计算机
111:cpu
112:主存储器
113:存储装置
114:输入接口
115:显示控制器
116:数据读取器/写入器
117:通信接口
118:输入装置
119:显示装置
120:存储介质
121:总线
- 还没有人留言评论。精彩留言会获得点赞!