一种镁合金材料本构关系模型的建立方法与流程

本发明属于镁合金材料塑性变形本构模型的建立方法，可以适用于不同牌号镁合金塑性变形本构模型的建立。

背景技术：

材料的本构模型是塑性变形数值模拟重要的基础理论，是工艺规程制定的重要参考要素。由于材料在塑性加工变形过程中的动态响应是材料内部组织演化过程引起的硬化与软化综合作用的结果，其本构关系是高度非线性的。目前普遍的做法是通过数学处理方法依据arrhennius方程对恒条件下变形的实验数据进行拟合来建立本构关系。用来表征镁合金单向拉伸、压缩变形的本构模型已在不同变形条件下建立，预测精度不高是这些模型存在的普遍问题，然而尚未提出有效的解决办法。本发明专利就是针对当前镁合金已有本构模型预测精度低的技术问题，提出了一种高预测精度的镁合金材料本构关系模型的建立方法。

技术实现要素：

本发明专利的目的就是根据镁合金的高温压缩应力—应变关系，提供一种高预测精度的镁合金材料本构关系模型的建立方法

本发明是这样实现的，一种镁合金材料本构关系模型的建立方法的具体步骤如下：

步骤一、简化arrhennius方程

镁合金的本构方程采用弹塑性体关于双曲正弦模型的热变形方程，即修正后的arrhennius方程：

(1)

对于双曲正弦模型，将代入(1)式中进行简化，得出以下结论：

当时，，其相对误差小于1.48%。

(2)

当时，，其相对误差为0.46%~2.8%。

(3)

时，，其相对误差小于2.8%。

(4)

式中，—应变速率，s^-1；q—变形激活能，j/mol，与材料有关；—流变应力，mpa；n—应力指数；t—温度，k；r—摩尔气体常数，；a和为与材料有关的常数；。

步骤二、求解所有温度范围内的变形激活能q值

通过分析变形激活能随温度的变化规律可知，随着温度的增大变形激活能q值逐渐减小，但是下降趋势有所差别，某些温度范围呈现急剧性，而有些则较为平缓。当拟合整体温度范围下的本构方程时，传统的材料本构模型往往以所有温度下的变形激活能平均值作为材料的变形激活能值，这样会造成整体本构模型误差较大。

步骤三、划分温度范围建立本构方程

将整体变形温度范围根据变形激活能随温度变化规律分解为2—4个区间来分别建立本构方程。分别计算不同温度区间下的变形激活能q。对各温度区间分别建立镁合金本构模型。

进一步，所述求解所有温度范围内的变形激活能q值的具体方法与过程为：

①的求解

对式（2）和式（4）两边取对数得到

（5）

（6）

取所有温度、应变速率下的峰值应力(即一定变形温度、应变速率下应力的最大值)—应变速率值按式（5）和（6）进行线性拟合，做拟合直线图和，拟合直线斜率的均值分别为1/n和的值，1/n和两值相除便可求出。

②n的求解

对式（1）两边取对数得到

（7）

取所有温度、应变速率下的峰值应力—应变速率值按式（7）进行线性拟合，做拟合直线图，则拟合直线斜率倒数的平均值即为n的值。

③变形激活能q的求解

对式（7）改变形式

（8）

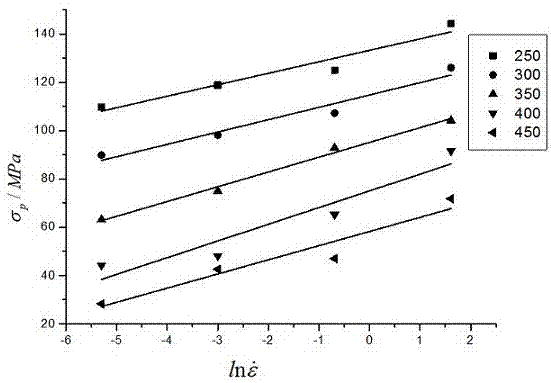
取所有温度、应变速率下的峰值应力σp-温度t值按式（8）进行线性拟合，做拟合直线图，则拟合直线的斜率的均值就是的值，

对式（7）改变形式

两边对1/t求导

（9）

将所求的和n值代入式（9）即可求出所有变形条件下的变形激活能q值。

所述划分温度范围建立本构方程的具体方法为：

①的求解

取所划分的某个变形温度范围内的峰值应力—应变速率值按式（5）和（6）进行线性拟合，做拟合直线图和，拟合直线斜率的均值分别为1/n和的值，1/n和两值相除便可求出。

②n的求解

取所划分的某个变形温度范围内的峰值应力-应变速率值按式（7）进行线性拟合，做拟合直线图，则拟合直线斜率倒数的平均值即为n的值。

③变形激活能q的求解

取所划分的某个变形温度范围内的峰值应力-温度t值按式（8）进行线性拟合，做拟合直线图，则拟合直线的斜率的均值就是的值。

将本具体方法所求的和②中所求n值代入式（9）即可求出所划分的某个变形温度范围内的的变形激活能q值。

④a，a1，a3的求解

本具体方法②中所得拟合直线的截距为，将本具体方法②和③中所求n和q值代入即可求出a的值，由式（2）和式（4）可求得，。

⑤n*，a2的求解

对式（3）两边取对数并将所求代入

（10）

取所划分的某个变形温度范围内的峰值应力-应变速率值按式（10）进行线性拟合，做拟合直线图，则拟合直线斜率的均值即为2n*的值，可求出n*。将③所求变形激活能q代入直线斜率即可求出a2。

根据该温度范围的峰值应力-应变速率数据，按照本划分温度范围建立本构方程的具体方法①~⑤即可确定a，a1，a2，a3，，n，n*，q值，由此可确定该温度范围的镁合金材料本构关系模型。同理，对于其它温度范围，按照相同的方法可确定其它温度范围的本构模型。

本发明专利的原理：

将镁合金材料加工成一定规格的圆柱体，在圆柱体上下端面涂抹润滑剂以消除试样与压头间的摩擦，通过热模拟试验机对材料进行等温压缩，热压缩压力与材料受挤压变形时的应力变化规律相同，因此可以用热模拟试验机压缩实验的应力—应变数据来建立材料的本构模型。

本发明的优点是：相对于传统的镁合金材料本构模型，通过本发明提供的方法建立的镁合金材料本构模型具有更高的预测精度。

附图说明

图1250℃~450℃下拟合直线图

图2250℃~450℃下拟合直线图

图3250℃~450℃下拟合直线图

图4不同应变速率（0.005~5s^-1）下拟合直线图

图5铸态az31b镁合金不同变形速率（0.005~5s^-1）下变形激活能与变形温度的关系曲线

图6250℃~300℃下拟合直线图

图7应变速率（0.005~5s^-1）下拟合直线图

图8250℃~300℃下拟合直线图

具体实施方式

下面结合实施例对本发明做进一步说明，可以知道，本实施例仅仅用以解释本发明，并不用于限定本发明。

本实施例选定某公司生产的铸态az31b镁合金，热模拟试验机采用gleeble1500热/动模拟试验机。将试样加工成圆柱试样，试样两端均匀地涂抹上机油用来润滑。在变形温度250~450℃、应变速率0.005~5s^-1下对试样进行等温压缩试验，得到不同温度、不同应变速率下的应力应变数据。

表1测得的不同变形条件下的峰值应力（mpa）

（1）简化arrhennius方程

简化后的arrhennius方程如下：

当时，，其相对误差小于1.48%。

(11)

当时，，其相对误差为0.46%~2.8%。

(12)

当时，，其相对误差小于2.8%。

(13)

式中，—应变速率，s^-1；q—变形激活能，j/mol，与材料有关；—流变应力，mpa；n—应力指数；t—温度，k；r—摩尔气体常数，；a和为与材料有关的常数，。

（2）求解变形激活能q值

①的求解

取表一中所有温度、应变速率下的峰值应力-应变速率值按式（5）和（6）进行线性拟合，做拟合直线图，如图1和图2，由拟合直线斜率均值求出，两值相除便可求出=0.0112。

②n的求解

取表1中所有温度、应变速率下的峰值应力-应变速率值按式（7）进行线性拟合，做拟合直线图，如图3，则拟合直线斜率倒数的平均值为n的值，得到n=11.3820。

表2各温度条件下所求n值

③变形激活能q的求解

对式（7）改变形式

（14）

取表1中所有温度、应变速率下的峰值应力-温度t值按式（14）进行线性拟合，做拟合直线图，如图4，则拟合直线的斜率的均值就是的值，结果如表3

表3各应变速率下值

对式（7）改变形式

两边对1/t求偏导

将所求的和n值代入即可求出所有变形条件下的变形激活能q值。

表4250~450℃下变形激活能值

绘制q-t图如图5，通过分析变形激活能随温度的变化规律可知，随着温度的增大变形激活能q值逐渐减小，但是下降趋势有所差别，300~350℃范围呈现急剧性，250~300℃和350~400℃范围则较为平缓。当拟合整体温度范围下的本构方程时，传统的材料本构模型往往以所有温度下的变形激活能平均值作为材料的变形激活能值，这样会造成整体本构模型误差较大。

步骤三、划分温度范围建立本构方程

根据变形激活能随温度的变化规律这里将变形温度分解为3个区间（250~300℃，300~350℃，350~450℃）来分别建立本构方程。

250~300℃范围本构方程求解

①的求解

取250~300℃范围内的峰值应力-应变速率值按式（5）和（6）进行线性拟合，做拟合直线图，由拟合直线斜率求出=24.2611和=0.2036，两值相除便可求出=0.0084。

②n的求解

取250~300℃范围内的峰值应力-应变速率值按式（7）进行线性拟合，做拟合直线图，如图6，则拟合直线斜率倒数的平均值为n的值，得到n=18.1549。

③变形激活能q的求解

取250~300℃范围内的峰值应力-温度t值按式（9）进行线性拟合，做拟合直线图，如图7，则拟合直线的斜率的均值就是的值，将上面所求n=18.1549代入即可求出该温度范围内的变形激活能q值，q=204950j/mol。

④a，a1，a3的求解

②中按式（7）进行拟合所得直线的截距为，将②和③中所求n和q值代入即可求出a=7.2415×10¹⁷，由式（2）和式（4）可求得=1.4974×10^-20，=2.4812×10¹²。

⑤n*，a2的求解

取250~300℃范围内的峰值应力-应变速率值按式（10）进行线性拟合，做拟合直线图，如图8，则拟合直线斜率的均值即为2n*的值，可求出2n*=36.3。将③所求变形激活能q代入直线斜率即可求出a2=6.79×10¹⁷。

将=0.0084、n=18.1549、q=204950、a=7.2415×10¹⁷、a1=1.4974×10^-20、a2=6.79×10¹⁷、a3=2.4812×10¹²代入则所求250~300℃范围的本构方程为：

同理，分别利用300~350℃和350~400℃范围内的峰值应力-应变速率值按照同样的求解过程可求出300~350℃和350~400℃范围的本构方程，结果如下：

300~350℃范围的本构方程为：

350~400℃范围的本构方程为：

。