一种基于实数编码量子进化算法的不规则排样方法与流程

本发明涉及玻璃切割、服装及皮革剪裁等加工领域中的计算机辅助排样技术领域，特别是涉及一种不规则形状的样片在宽度固定而长度不固定的矩形母板上的排样方法。

背景技术：
不规则多边形排样问题广泛地存在于金属冲裁、玻璃切割及服装、皮革剪裁等加工中，在批量生产中排样效率微小的提高，就可能为企业带来巨大的经济效益。目前，一些企业还是靠人工经验进行排样，不仅工作量大、效率低，且排样效果远不能满足生产需求，带来原材料的浪费。不规则形状排样问题的求解方法最早使用传统的数学方法或一些启发式算法，这些方法一般仅适用于小规模排样问题，难以满足实际需求；目前大部分排样问题主要采用人工智能的方法来求解，如遗传算法、模拟退火算法或粒子群算法等，在实践中，这些方法的局部搜索能力和全局搜索能力很难达到平衡，从而导致排样时间长、排样的搜索精度低及原材料的利用率低的问题。2002年提出的量子进化算法使用量子比特对个体编码，量子染色体可表示多个模态解的叠加，具有全局搜索能力强、不易陷入局部最优等优点，在解决利用遗传算法求解不理想的问题时表现出了优异的性能。目前量子进化算法已广泛应用于多重二次背包问题、柔性作业车间调度问题和多目标随机需求车辆路径问题等众多领域的优化问题，表现出了优异的性能。迄今为止，国内外少有将量子进化算法应用到二维不规则排样领域的相关研究。

技术实现要素：
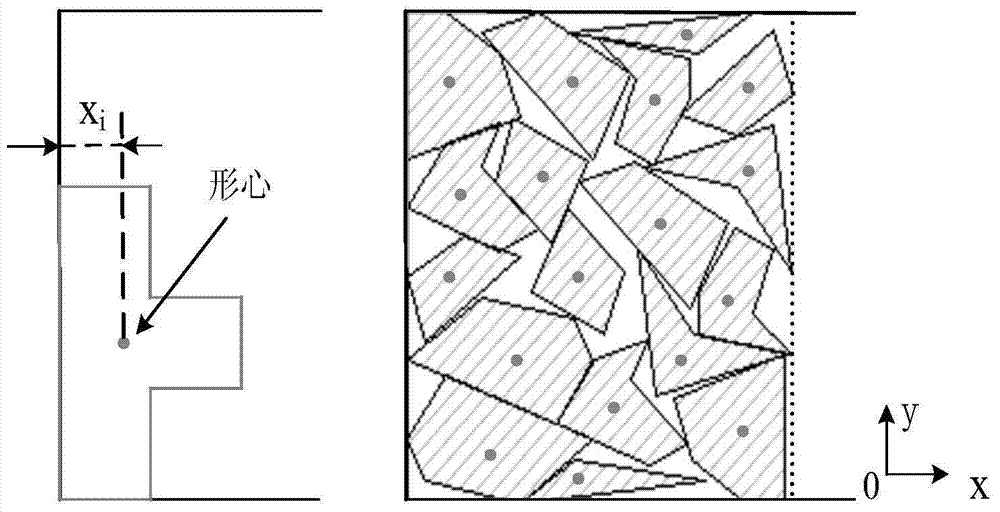
本发明要解决现有排样方法排样时间长、排样的搜索精度低及原材料的利用率低的问题，而提出一种基于实数编码量子进化算法的不规则排样方法。本发明解决其技术问题所采用的技术方案是：一种基于实数编码量子进化算法的不规则排样方法，包括以下步骤：步骤1、实数编码，采用实数量子几率幅值对排样编号序列和旋转角度序列进行统一编码，对于具有n个排样件和每个排样件允许沿顺时针方向旋转m个角度的排样问题，用n×(n+m)的二维量子位概率幅矩阵表示第t代第k个量子染色体为：式中，inf为无穷大数，βij(0≤i≤n-1,1≤j≤i+1)用来编码排样件的编号,β′iu(0≤i≤n-1,1≤u≤m)用来编码排样件的旋转角度索引；步骤2、系统初始化，利用不规则形状样片的几何特征，构造启发式算法生成初始排样序列种群U(0)及第0代的量子种群Q(0)；步骤3、计算U(0)中各个个体的适应度，将最优个体赋值给初始种群最优个体步骤4、种群更新，进化迭代次数t＝t+1，采用量子旋转门更新量子染色体种群，得到第t代的量子种群Q(t)；步骤5、量子观测，对种群Q(t)分别进行排样编号序列量子观测与旋转角度索引序列量子观测，生成排样序列种群U(t)；步骤6、利用基于临界多边形(NFP)的不规则样片形心最低的放置策略将由种群U(t)确定的排样顺序将样片排入母板，然后进行个体适应度评价，将其中的最优个体赋值给第t代种群最优个体步骤7、判断迭代次数t是否达到预先设定的数目，若否转步骤3，是则输出当前最优个体算法结束。进一步，所述步骤2中，系统初始化参数包括最大迭代代数，量子旋转门初始旋转角度，变异间隔代数。进一步，所述步骤4中，如果在连续n代迭代过程中没有找到更优解，则对Q(t)中的各个个体进行量子变异操作。更进一步，所述步骤6中，基于NFP的不规则样片形心最低的放置策略如下：以样片的形心坐标作为参考点来构造形心NFP，放置时选取形心NFP中具有最小横坐标值的顶点作为排样件的放置位置，再由多边形的拓扑关系确定其他各个顶点的具体排放位置。在进行排样时，优化的目标是在满足约束条件下使原材料的利用率η最高，即：式中，s(i)为第i个样片的面积。本发明与已有技术相比，具有如下优点与有益效果：1、将实数编码量子进化算法应用到计算机排样技术领域，实数编码方式减少了染色体编码长度，有效地缩短了排样时间；2、量子观测过程始终保持概率运算，解码效率高，提高了排样的搜索精度；3、通过构造启发式算法生成高质量的初始种群，提高了算法的优化能力，提高了原材料的利用率。附图说明图1为本发明方法的流程图。图2为不规则多边形形心与排样放置策略示意图。图3为通用二维不规则多边形排样基准用例Blaz1基于本发明的排样效果示意图。具体实施方式下面结合附图对本发明作进一步的描述。参考图1～图3，一种基于实数编码量子进化算法的不规则排样方法，包括以下步骤：步骤1、H＝[h(1),h(2),…h(n)](1≤h(i)≤n)为n个排样件的排样编号序列，T＝[δ(1),δ(2),…,δ(n)]为排样件的旋转角度序列，采用实数量子几率幅值对排样编号序列和旋转角度序列进行统一编码，对于具有n个排样件和每个排样件允许沿顺时针方向旋转m个角度的排样问题，用n×(n+m)的二维量子位概率幅矩阵表示第t代第k个量子染色体为：式中，inf为无穷大数，βij(0≤i≤n-1,1≤j≤i+1)用来编码排样件的编号,β′iu(0≤i≤n-1,1≤u≤m)用来编码排样件的旋转角度索引；步骤2、不规则形状的排样样具有如下几何方面的特征：①面积较大的排样件放置后产生的孔洞较大，反之面积较小的放置后产生的孔洞较小；②较大的孔洞通常可以装入面积较小的排样件；③几何相似度较高的排样件放置在一起，有利于提高原材料的填充率。利用上述不规则形状样片的几何特征，构造启发式算法生成初始排样序列种群的步骤可描述为：初始化生成一个初始排样序列X；按面积从大到小的顺序样片进行排序，根据排序结果调整序列X；按照排样件几何相似度较高(大于0.8)则放置在一起的原则，调整X；按X确定的顺序和旋转角度放置排样件，若排放某样片后形成的孔洞面积足以容纳较小的样片，则调整二者的顺序；对X执行反转变异；反复执行上述步骤得到数量为N的初始排样序列种群。同时初始化如下系统参数：最大迭代代数，量子旋转门初始旋转角度，变异间隔代数。步骤3、计算U(0)中各个个体的适应度，将最优个体赋值给初始种群最优个体原材料的利用率η定义为：因此，定义个体的适应度评价函数为：如果f(x)值越大，则表示个体的排样布局越优。步骤4、进化迭代次数t＝t+1，采用量子旋转门更新量子染色体种群，得到第t代的量子种群Q(t)；量子旋转角采用动态自适应旋转角调整策略，令为中第i行第j列元素对应的旋转角，定义式中：fmax和favg分别为当前种群最优适应度和平均适应度，f(x)为当前个体适应度，因此量子的更新操作为：在量子进化过程中，如果最优解在连续n代迭代过程中没有找到更优解，则对种群中的各个个体进行量子变异操作。采用量子非门对量子染色体实现变异操作，过程为：令a,b＝random[1,n+m](1≤a<b≤n+m)，对中的任意第i行(0≤i≤n-1)中的中的各个元素(除去几率幅值为inf的元素)施加量子非门变换，扰动方式如下：步骤5、量子观测，对种群Q(t)分别进行排样编号序列量子观测与旋转角度索引序列量子观测，排样编号序列量子观测方法为：(1)令i＝1，以元素inf产生一个初始向量A＝[α(n-1),α(n-2),…,α(1)]；(2)j＝random[1,i+1]，产生随机数rand,rand∈[0,1]；(3)若rand>|βij|2，则a(i)＝j-1，转(4)，否则转(2)；(4)i＝i+1，如果i≤n-1则转(2)；(5)完成向量集合A的赋值；(6)由A得到排样编号序列。旋转角度索引序列量子观测方法为：首先定义编号为i的排样件选择旋转角度为r(u)的概率为：(1)令i＝1；(2)令u＝1,sum＝0；(3)sum＝sum+piu；(4)产生随机数rand∈[0,1]，若rand<sum，则k(i)＝u，转(6)；(5)u＝u+1，如果u≤m则转(3)；(6)令i＝i+1，如果i≤n则转(2)；(7)输出旋转角度索引序列。步骤6、参考图2，基于临界多边形(NFP)的不规则样片形心最低的放置策略为：以样片的形心坐标作为参考点来构造形心NFP，放置时选取形心NFP中具有最小横坐标值的顶点作为排样件的放置位置，再由多边形的拓扑关系确定其他各个顶点的具体排放位置。根据此策略将种群U(t)确定的排样顺序将样片排入母板，然后进行个体适应度评价，同时将其中的最优个体赋值给第t代种群最优个体步骤7、判断迭代次数t是否达到预先设定的数目，若否转步骤3，是则输出当前最优个体算法结束。参考图3，本发明对通用二维不规则多边形排样基准用例Blaz1的排样效果图(材料宽度：15，样片数：28；迭代次数：83；排样高度：27.03，材料利用率：80.10％)。系统初始化参数设置为：最大迭代代数为150，量子旋转门初始旋转角度为0.01π，变异间隔代数为10，inf可以取值为10000。以上结合附图对本发明的具体实施方式作了说明，但这些说明不能被理解为限制了本发明的范围，本发明的保护范围由随附的权利要求书限定，任何在本发明权利要求基础上的改动都是本发明的保护范围。