对基于矩阵的分布式编程语言进行自动优化的方法与流程

本发明涉及大数据处理技术领域，特别涉及一种对基于矩阵的分布式编程语言进行自动优化的方法。

背景技术：

传统的基于矩阵的编程语言，比如说MATLAB、R等，能够用一种紧凑的方法表达对数据的操作。因此，他们被广泛地应用于数据分析和科学计算领域。为了保证这些语言的易用性，并同时能够通过增加机器数目进行线性扩展，很多工具被研究人员们提出。这些工具一般来说会提供一个与上述语言相似的基于矩阵的编程接口，同时它们的底层实现会基于MapReduce等大数据编程模型。通过自动地将这两种模型进行转换得到既保留上层语言的可编程性，又能够做到扩展以及容错的系统。然而，由于这些面向于MapReduce的底层系统缺乏相应的原语，它们执行矩阵运算时的效率并不高，并且通讯量也很大，因此并不是一个合适的方法。

由于上述的问题，后续的研究人员尝试开发了直接基于分布式矩阵操作的分布式计算框架。这些框架(比如Spartan，ComBLAS等)将数据描述为一维或多维的数组，并利用矩阵计算原语对它们进行操作。由于利用了目前已有的一些技术实现，比如2.5D矩阵乘法、分片等，它们得以获得了很高的运行效率。根据它们的测评结果，这一类的计算框架一般都远快于传统的计算框架(至少10倍的效率提升)。

然而，这样的体系结构仍然是不完美的。有一类重要的组件不存在于这一类结构之中，即优化器。优化器应该要可以通过讲操作进行合并或者调整操作间的顺序等办法对程序进行优化。相对地，目前的这一类系统基本上都采取的是最简单的实现方法，既完全按照程序员所给定的步骤，一步一步地执行，这就好像是在程序编译的时候加上了–O0选项一样。这一状况昭示了在这一部分仍然有很大的优化空间。举例来说Spartan系统采用了一个很简单的优化策略，既将相邻的多个Map操作或者Map－Reduce对组合到一个函数中去一起执行。根据它们的测试，这样简单的优化就能够取得最高达到两倍的优化。

虽然在传统的单机领域对基于矩阵的编程语言进行优化是一个已经被研究了很多年的话题，但在多机领域仍然没有先例。在多极情况下优化器必须考虑到数据间的同步情况，因此并不能进行任意的跳换按顺序。根据相关研究发现，现有的方法主要面临着以下几个问题：1)现有的编程模型要么过于局限以至于有很大一类的算法不能够被支持，要没过于广泛以至于无法进行有效的优化；2)利用传统的基于矩阵的语言进行编程的时候会产生很多的中间结果数组，需要对他们进行合并处理；3)数据同步的顺序需要仔细考虑，从而减少网络通讯的开销。

技术实现要素：

本发明旨在至少在一定程度上解决上述相关技术中的技术问题之一。

为此，本发明的目的在于提出一种对基于矩阵的分布式编程语言进行自动优化的方法，该方法可以自动地对给定的基于矩阵的程序进行优化，通过减少内存的读取与写入，提升缓存的利用率，减少通讯量等手段将程序的运行效率提升。

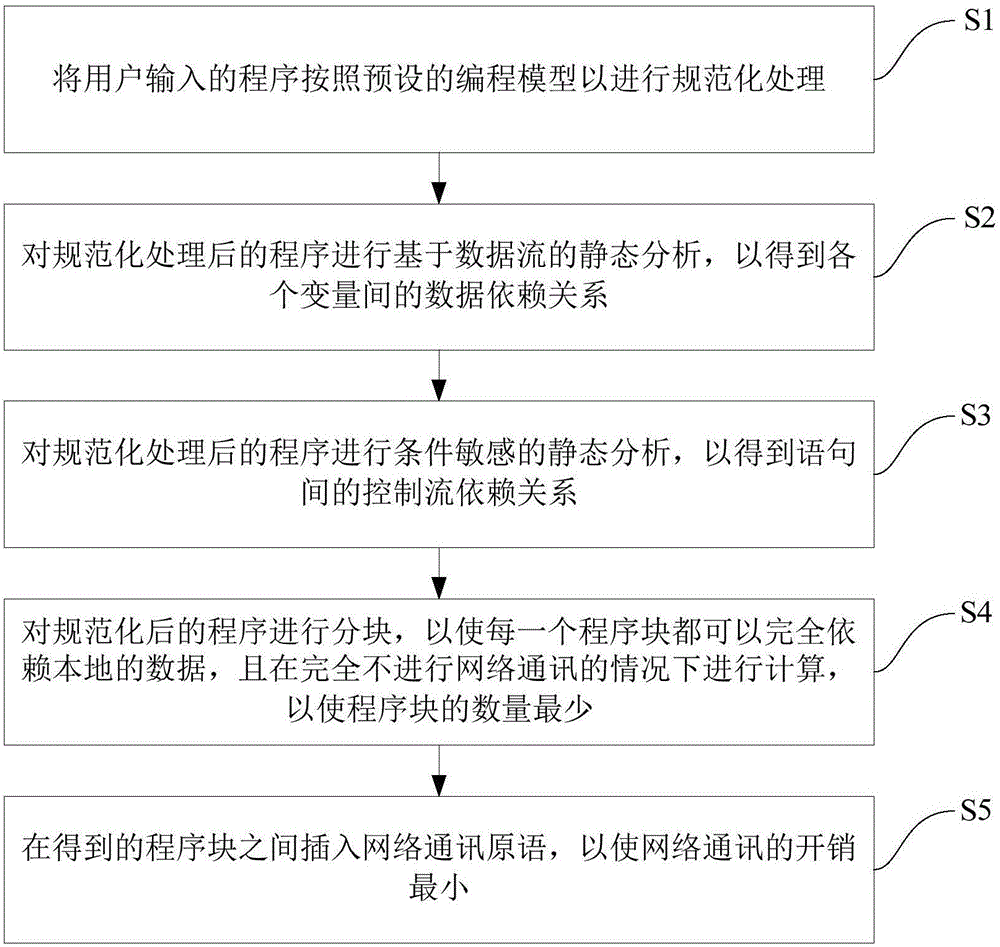
为了实现上述目的，本发明的实施例提出了一种对基于矩阵的分布式编程语言进行自动优化的方法，包括以下步骤：S1：将用户输入的程序按照预设的编程模型进行规范化处理；S2：对规范化处理后的程序进行基于数据流的静态分析，以得到各个变量间的数据依赖关系；S3：对规范化处理后的程序进行条件敏感的静态分析，以得到语句间的控制流依赖关系；S4：对规范化后的程序进行分块，以使每一个程序块都可以完全依赖本地的数据，且在完全不进行网络通讯的情况下进行计算，以使程序块的数量最少；以及S5：在得到的程序块之间插入网络通讯原语，以使所述网络通讯的开销最小。

根据本发明实施例的对基于矩阵的分布式编程语言进行自动优化的方法，可以自动的对给定的基于矩阵的程序进行优化，通过减少内存的读取与写入，提升缓存的利用率，减少通讯量等手段将程序的运行效率提升。

另外，根据本发明上述实施例的对基于矩阵的分布式编程语言进行自动优化的方法还可以具有如下附加的技术特征：

在一些示例中，所述预设的编程模型为KASEN编程模型，所述KASEN编程模型为自定义的编程模型，具有如下特征：对局部变量和全局变量的区分，并且规定局部变量仅可通过局部变量计算得出，全局变量仅可通过全局变量计算得出；定义了完全分开的网络通讯及计算原语；定义了两类共4个不同的计算原语，其中，vector-only类的原语包括Map，Reduce和ZipWith；matrix-vector类的原语包括MxV，所述S1进一步包括：所述KASEN编程模型通过定义Local类变量、Shared类变量、Vector类变量和Matrix类变量对数据进行存储，其中，Local类变量表示的是局部数据，每一个Local类变量在各个机器上都各自有一份实例，并且这些实例之间不需要进行同步，Shared类变量表示的是一种全局变量，每一个Shared类变量在各个机器上也都各自有一份实例，并且Shared类变量的值需要实时保持同步，各个机器上的Shared变量的值必须相等，Vector类变量同样是一种全局变量，且Vector类变量中的每一个元素只会被存储在一个机器之上，Matrix类变量也是一种分布式的存储在集群中的全局变量，其存储方式由用户预先设定；所述KASEN编程模型通过定义Map操作、Reduce操作、ZipWith操作和MxV操作对数据进行相应操作，其中，Map操作的输入和输出分别是一个数组，系统将给定的用户函数应用于输入数组的每一个元素上，以得到输出数组，Reduce操作的输入为一个数组，但输出仅为一个标量，系统利用用户给定的归并函数不断的将输入数组的数据归并，直至得到最终的结果，将所述最终的结果作为所述标量，ZipWith操作的输入为两个数组，输出为一个数组，系统将用户给定的函数应用于两个输入数组中下标相等的两个元素中从而得到相应的输出，MxV操作执行类似于线性代数中矩阵与向量的乘积操作，将输入的一个数组和一个矩阵相乘得到结果数组。

在一些示例中，还包括：所述编程模型提供两种不同的网络原语，分别为gather和scatter，其中，所述gather用于将分布式状态下的全局变量转换成集中式的存储；所述scatter用于将集中式存储的变量转换成分布式状态。

在一些示例中，所述S2进一步包括：对规范化处理后的程序进行流敏感的数据流分析，以得到每一个变量的always-depended信息和may-depended信息，其中，所述always-depended信息为一个变量的集合，在该集合中的所有变量，无论输入数据如何都会被该输入数据所依赖，所述may-depended信息为一个变量的集合，在该集合中的所有变量，在特定的条件下会被输入数据所依赖；根据所述always-depended信息和may-depended信息得到所述规范化处理后的程序中各个变量间的依赖关系。

在一些示例中，所述S3进一步包括，对于一个变量，判断所述变量相关的语句是否可以执行或已经执行了：1)判断所述语句没有任何属于may-depended类的依赖关系，2)判断所述语句的所有的属于always-depended类的依赖关系是否已经被执行或者可以执行了，并根据判断结果得到变量相关的语句的控制依赖关系。

在一些示例中，所述S4进一步包括：根据所述always-depended信息和may-depended信息将所述规范化处理后的程序建模成一个数据库可用性组(Database Availability Group，DAG)，并对所述数据库可用性组DAG进行等价的变化；对每一种变换得到的DAG进行分块，以使每一个程序块都可以完全依赖本地的数据，并在完全不进行网络通讯的情况下进行计算；枚举所有可能的变换形式，以得到最优的结果。

在一些示例中，网络通讯模式为eager或lazy，其中，所述eager在计算前同步所有数据，所述lazy在计算后同步所有数据。

在一些示例中，所述S5进一步包括：S51：尝试将相应的网络原语gather和scatter插入到所有计算的执行之前，并计算相应的通讯和计算开销之和；S52：尝试将相应的网络原语gather和scatter插入到所有计算的执行之后，并计算相应的通讯和计算开销之和；S53：比较所述S51中得到的开销之和及所述S52中得到的开销之和，选择其中开销之和较小的方式执行。

本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

附图说明

本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：

图1是根据本发明实施例的对基于矩阵的分布式编程语言进行自动优化的方法的流程图；

具体实施方式

下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，仅用于解释本发明，而不能理解为对本发明的限制。

以下结合附图描述根据本发明实施例的对基于矩阵的分布式编程语言进行自动优化的方法。

图1是根据本发明一个实施例的对基于矩阵的分布式编程语言进行自动优化的方法的流程图。如图1所示，该方法包括以下步骤：

步骤S1：将用户输入的程序按照预设的编程模型进行规范化处理，从而使得对用户编写的程序进行精确的静态分析成为可能。

具体地说，在本发明的一个实施例中，上述预设的编程模型为KASEN编程模型，该编程模型的特征例如包括：1)对局部变量和全局变量的区分，并且规定局部变量仅可通过局部变量计算得出，全局变量仅可通过全局变量计算得出。这一规定明确地规范了数据同步所能发生的区域，从而方便了后续程序分析的进行；2)定义了完全分开的网络通讯及计算原语，即计算时所有的数据均在本地可以获得，因此不会出现计算和通讯同时进行的情况；3)定义了两类共4个不同的计算原语。其中，vector-only类的原语包括Map，Reduce和ZipWith；matrix-vector类的原语包括MxV。

需要说的是，经过大量研究发现，大多数的机器学习和数据发掘的算法都可以很简单的通过本发明实施例定义的这种编程模型进行描述。因此，可以认为，本发明实施例的编程模型并没有降低程序语言的可编性。

更为具体地，上述预设的编程模型KASEN可以由以下的数据模型、计算模型、和通讯模型三个部分进行定义。具体为：

首先，在编程模型方面允许用户定义两类共四种类型的变量。KASEN编程模型通过定义Local类变量、Shared类变量、Vector类变量和Matrix类变量对数据进行存储，其中，Local类变量表示的是局部数据，每一个Local类变量在各个机器上都各自有一份实例，并且这些实例之间不需要进行同步，Shared类变量表示的是一种全局变量，与Local类变量相似，每一个Shared类变量在各个机器上也都各自有一份实例，但不同的是，Shared类变量的值需要实时保持同步，即各个机器上的Shared变量的值必须相等，Vector类变量同样是一种全局变量，但与Shared类变量不同的地方在于，Vector类变量中的每一个元素只会被存储在一个机器之上，Matrix类变量也是一种分布式的存储在集群中的全局变量，其存储方式由用户预先设定。

在通过如上述的数据模型定义好数据的存储后，KASEN编程模型通过定义Map操作、Reduce操作、ZipWith操作和MxV操作对数据进行相应操作。其中，Map操作的输入和输出分别是一个数组，系统将给定的用户函数应用于输入数组的每一个元素上，以得到输出数组；Reduce操作的输入为一个数组，但输出仅为一个标量，系统利用用户给定的归并函数不断的将输入数组的数据归并，直至得到最终的结果；ZipWith操作的输入为两个数组，输出为一个数组，系统将用户给定的函数应用于两个输入数组中下标相等的两个元素中从而得到相应的输出；MxV操作执行类似于线性代数中矩阵与向量的乘积操作，将输入的一个数组和一个矩阵相乘得到结果数组。

最后，上述的编程模型会提供两种不同的网络原语，分别是gather和scatter。其中，gather用于将分布式状态下的全局变量转换成集中式的存储；scatter用于将集中式存储的变量转换成分布式状态。

步骤S2：对规范化处理后的程序进行基于数据流的静态分析，以得到各个变量间的数据依赖关系。

具体地说，步骤S2进一步包括：对规范化处理后的程序进行流敏感的数据流分析，以得到每一个变量的always-depended信息和may-depended信息，其中，always-depended信息为一个变量的集合，在该集合中的所有变量，无论输入数据如何都会被该输入数据所依赖，always-depended信息为一个变量的集合，在该集合中的所有变量，在特定的条件下会被输入数据所依赖；根据always-depended信息和may-depended信息得到规范化处理后的程序中各个变量间的依赖关系。

其中，在步骤S2中，例如使用常用的迭代类算法，由每个块的近似入口状态信息出发，然后应用转移函数基于这些入口状态信息计算出口状态信息，然后，使用连接运算符更新入口状态信息，最后两步将一直进行下去直至到达不动点，即此时入口状态信息和出口状态信息都不再改变。

步骤S3：对规范化处理后的程序进行条件敏感的静态分析，以得到语句间的控制流依赖关系。

具体地说，对于一个变量，判断所述变量相关的语句是否可以执行或已经执行了它没有任何属于may-depended类的依赖关系和它所有的属于always-depended类的依赖关系，并根据判断结果得到所述变量相关的语句的控制依赖关系。换言之，对于一个变量，其相关的语句已经可以执行了等价于：1)它没有任何属于may-depended的依赖关系；2)它所有的属于always-depended类的依赖关系都已经被执行或者可以被执行了。通过上述条件就可以很简单的判断一条语句的控制依赖关系。

步骤S4：对规范化后的程序进行分块，以使每一个程序块都可以完全依赖本地的数据，且在完全不进行网络通讯的情况下进行计算，以使程序块的数量最少。

具体地说，步骤S4进一步包括：根据always-depended信息和may-depended信息将规范化处理后的程序建模成一个数据库可用性组DAG，并对数据库可用性组DAG进行等价的变化；对每一种变换得到的DAG进行分块，以使每一个程序块都可以完全依赖本地的数据，并在完全不进行网络通讯的情况下进行计算；最终通过枚举所有可能的变换形式，以得到最优的结果。

步骤S5：在得到的程序块之间插入网络通讯原语，以使网络通讯的开销最小。在本发明的一个实施例中，最优的网络通讯模式例如为eager或lazy，其中，eager在计算前同步所有数据，lazy在计算后同步所有数据。基于此，步骤S5进一步包括：

S51：尝试将相应的网络原语gather和scatter插入到所有计算的执行之前，并计算相应的通讯和计算开销之和。

S52：尝试将相应的网络原语gather和scatter插入到所有计算的执行之后，并计算相应的通讯和计算开销之和。

S53：比较S51中得到的开销之和及S52中得到的开销之和，选择其中开销之和较小的方式执行。

综上，根据本发明实施例的对基于矩阵的分布式编程语言进行自动优化的方法，可以自动的对给定的基于矩阵的程序进行优化，通过减少内存的读取与写入，提升缓存的利用率，减少通讯量等手段将程序的运行效率提升。并且在具体示例中，经过测试得到，本发明实施例的方法可以提供最高达到5.8倍的加速比。其中，经测试，在PageRank算法上的加速度最高达到2.2倍；在Black-Scholes算法上的加速度最高达到1.9倍；在K-Means算法上的加速度最高达到5.8倍；在LBFGS算法上的加速度最高达到3.5倍。

在本发明的描述中，需要理解的是，术语“中心”、“纵向”、“横向”、“长度”、“宽度”、“厚度”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”“内”、“外”、“顺时针”、“逆时针”、“轴向”、“径向”、“周向”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。

此外，术语“第一”、“第二”仅用于描述目的，而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括至少一个该特征。在本发明的描述中，“多个”的含义是至少两个，例如两个，三个等，除非另有明确具体的限定。

在本发明中，除非另有明确的规定和限定，术语“安装”、“相连”、“连接”、“固定”等术语应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或成一体；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连，可以是两个元件内部的连通或两个元件的相互作用关系，除非另有明确的限定。对于本领域的普通技术人员而言，可以根据具体情况理解上述术语在本发明中的具体含义。

在本发明中，除非另有明确的规定和限定，第一特征在第二特征“上”或“下”可以是第一和第二特征直接接触，或第一和第二特征通过中间媒介间接接触。而且，第一特征在第二特征“之上”、“上方”和“上面”可是第一特征在第二特征正上方或斜上方，或仅仅表示第一特征水平高度高于第二特征。第一特征在第二特征“之下”、“下方”和“下面”可以是第一特征在第二特征正下方或斜下方，或仅仅表示第一特征水平高度小于第二特征。

在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不必须针对的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任一个或多个实施例或示例中以合适的方式结合。此外，在不相互矛盾的情况下，本领域的技术人员可以将本说明书中描述的不同实施例或示例以及不同实施例或示例的特征进行结合和组合。

尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。