一种基于配点理论的高维随机热传导问题谱分析方法与流程

本发明属于机械工程领域，具体涉及一种基于配点理论的高维随机热传导问题谱分析方法。

背景技术：

在生产实践活动中，通过物体直接接触进行热量传递的热传导是一种极其普遍的物理现象。尤其是在航空航天等工业装备以及电子器件等精密产品的生产制造过程中，如何有效的实现热量传递，已成为产品设计的一个重要方面。而这类问题的关键首先要确定系统温度场的分布规律。现有关于热分析的许多研究都是针对确定性模型进行的，而实际工程中，由于制造工艺的限制、测量的误差以及认知的局限，结构的材料属性、外部载荷和边界条件等物理参数不可避免的受到多种不确定因素的影响，使得系统的温度响应也表现出一定的不确定性，这就使得传统基于确定性模型的传热数值计算方法不够准确。

事先通过试验信息确定模型输入参数的概率分布规律，随机不确定模型将系统中的不确定性看作随机变量或随机过程，进而利用概率论和统计方法研究不确定性传播规律。随机建模及数值计算方法具有成熟的理论基础，在不确定分析领域发挥了重要作用。以蒙特卡洛抽样、随机摄动法、矩分析为代表的随机数值计算方法在不确定结构的静、动力特性分析方面已经取得了不少研究成果，但在传热领域的应用还十分有限。另外，传统的蒙特卡洛抽样方法，通过数字模拟和统计分析来求取系统响应的概率特征。尽管操作简单，但其计算精度依赖于大量的抽样实验，因此很难应用于复杂的工程系统。随机摄动方法计算量小，但由于忽略了部分高阶项，计算精度难以满足工程需求。对于不确定参数较多的情况，矩分析方法需要求解大量耦合方程，计算量大，并且计算误差难以估计。因此，如何建立准确高效的随机分析方法对高维不确定传热问题进行数值求解，是目前学术领域的一个研究热点，对于弥补现有传热数值计算方法的不足，具有重要的工程应用价值。

技术实现要素：

本发明所要解决的技术问题为：克服现有技术在热传导问题数值求解中存在的不足，充分考虑热传导模型中输入参数的随机不确定性，基于正交多项式逼近理论和配点分析技术，提出了一种有效求解随机温度响应均值、标准差等概率特征的数值计算方法，可系统化解决含有不确定参数的高维随机热传导问题，有效提高了随机有限元数值方法的计算精度和计算效率。

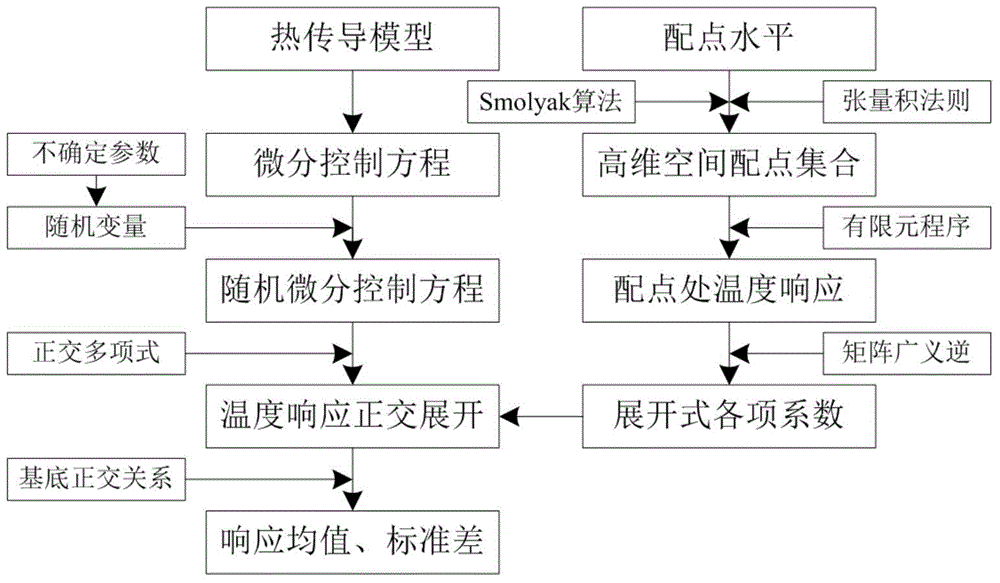
本发明为解决上述技术问题采用的技术方案为：一种基于配点理论的高维随机热传导问题谱分析方法，包括以下步骤：

步骤一：根据传热模型建立稳态热传导问题的微分控制方程；

步骤二：用随机变量表示传热模型中的不确定输入参数，根据步骤一中的微分控制方程建立热传导问题的随机微分控制方程；

步骤三：根据步骤二中随机变量的分布类型选用正交多项式，对步骤二随机微分控制方程中涉及的温度响应进行近似表示，得到随机温度响应的正交展开式；

步骤四：设定配点水平，利用张量积法则和smolyak(斯莫利亚克)算法构造高维不确定空间的配点集合；

步骤五：利用有限元程序计算步骤四配点集合中所有配点处的温度响应；

步骤六：根据步骤五中所有配点处的温度响应，建立步骤三随机温度响应正交展开式中各项系数的线性方程组，并利用矩阵广义逆进行求解，得到各项系数的一组值；

步骤七：将步骤六中得到的各项系数的一组值代回到步骤三随机温度响应正交展开式中，根据正交多项式基底函数的正交关系，计算随机温度响应的均值和标准差。

其中，所述步骤二中用随机变量表示传热模型中的不确定输入参数时，随机变量的数量和分布类型并不是固定不变的，与实际传热模型中不确定输入参数的数量特征和分布规律保持一致。

其中，所述步骤三中利用正交多项式对步骤二随机微分控制方程中涉及的温度响应进行近似表示时，正交多项式的类型和截断阶数并不是固定不变的，根据随机变量分布类型和逼近精度要求进行选取，例如正态分布的随机变量对应埃尔米特正交多项式，指数分布的随机变量对应拉盖尔正交多项式，另外正交多项式截断阶数越高，逼近精度就越高。

其中，所述步骤四中高维不确定空间配点集合的建立并不是固定不变的，根据计算耗费和计算精度的要求来设定配点水平，配点水平越高，计算精度就越高，而计算耗费就越大。

上述各步骤具体包括以下过程：

步骤一：根据传热模型建立稳态热传导问题的微分控制方程；

其中x为物理坐标，t(x)为温度响应，k(x)为热传导系数，f(x)为系统的热源强度。

步骤二：用随机变量ξ1,ξ2,...,ξn表示传热模型中的不确定输入参数，并记为向量的形式ξ＝(ξ1,ξ2,...,ξn)，其中n为不确定参数的数量。于是步骤一中热传导问题的微分控制方程可改写为随机微分控制方程

步骤三：根据步骤二中随机变量的分布类型选用对应的正交多项式，将步骤二随机微分控制方程中涉及的温度响应t(x；ξ)进行近似表示，得到随机温度响应的正交展开式

其中φi(ξ)为事先选定的正交多项式基底函数，ti(x)为对应的各项系数，多维指标i可表示为i＝(i1,i2,...,in)且满足|i|＝i1+i2+...+in，n为正交多项式的截断阶数。上述正交多项式中展开项的个数可用随机变量数n和截断阶数n按组合公式来计算。

步骤四：设定配点水平，利用张量积法则和smolyak算法构造高维不确定空间的配点集合。首先，对于随机变量ξj而言，确定其主要分布区间其中ξj和表示下界和上界。其次，将配点水平设定为k，令l＝k+n，则根据张量积法则和smolyak算法构造n维不确定空间的配点集合θ：

其中∪为并集运算的符号；ijj＝1,2,...,n表示第j个随机变量ξj在分布区间上的配点水平；表示第j个随机变量ξj对应配点水平ij在分布区间上的所有配点组成的集合，其配点数量和配点位置分别为：

其中和表示区间的中点和半径。

设上述配点集合θ中的配点总数为m，因此配点集合可具体表示为的形式，其中上标node表示配点。

步骤五：利用有限元程序计算步骤四配点集合中所有配点处的温度响应。首先，在配点处，步骤二中随机微分控制方程可具体表示为：

接着，利用现有的有限元程序对上述方程进行求解，可以得到步骤四配点集合θ中所有配点处的温度响应

步骤六：根据步骤五中所有配点处的温度响应建立步骤三随机温度响应正交展开式中各项系数ti(x)的线性方程组：

利用矩阵广义逆对此线性方程组进行求解，得到各项系数ti(x)的一组值。

步骤七：将步骤六中得到的各项系数ti(x)的一组值代回到步骤三随机温度响应正交展开式中，根据正交多项式基底函数φi(ξ)的正交关系，可以快速得到随机温度响应t(x；ξ)的均值e[t(x；ξ)]和标准差σ[t(x；ξ)]：

e[t(x；ξ)]≈e[tn(x；ξ)]＝t1(x)

本发明与现有技术相比的优点在于：

(1)与传统的热传导分析技术相比，所提出的随机模型和谱分析方法充分计及传热系统中输入参数的不确定性，计算结果对结构温度场分析具有更重要的指导意义。

(2)利用正交多项式对随机温度响应进行近似表示，可有效提高逼近精度。同时，利用基底函数的正交关系，可快速得到随机温度响应均值、标准差等概率特征。

(3)利用张量积法则和smolyak算法构造高维不确定空间的配点集合，在可有效求解正交展开式各项系数的前提下，进一步减少了所需的配点数量。

(4)本发明操作简单，实施方便，有效提高了随机分析方法的计算精度和计算效率。

附图说明

图1为本发明的一种基于配点理论的高维随机热传导问题谱分析方法流程图；

图2为本发明的三维夹芯传热结构有限元模型示意图。

具体实施方式

下面结合附图和实施例对本发明做进一步说明。

本发明适用于含有随机不确定参数的热传导问题温度响应计算。本发明实施方式以某三维夹芯传热结构模型为例，具体说明所述的一种基于配点理论的高维随机热传导问题谱分析方法。另外，此三维夹芯传热结构模型的随机温度响应谱分析方法可以推广到其他含有随机不确定参数的热传导问题温度响应计算中。

一种基于配点理论的高维随机热传导问题谱分析方法的计算过程如图1所示，建立热传导问题的微分控制方程，用随机变量表示不确定输入参数，改写热传导问题的微分控制方程为随机微分控制方程，利用正交多项式对随机温度响应进行近似表示，根据张量积法则和smolyak算法构造高维不确定空间的配点集合，并利用有限元程序计算所有配点处的温度响应，基于矩阵广义逆，求得温度响应正交展开式中的各项系数，最终根据基底函数的正交关系计算随机温度响应的均值和标准差。可分为如下几个步骤进行：

步骤一：考虑如图2所示的三维夹芯传热结构有限元模型，外面板5和内面板6离散为640个四边形单元，腹板7划分为720个四边形单元，上下面板采用热传导系数为k1的结构材料，而腹板材料的热传导系数为k2，外表面8施加热流载荷qs，内面板6与周围环境发生表面换热，环境温度为te，表面换热系数记为h，选定编号为1～4的四个节点作为此结构温度场的观测点。根据传热模型建立稳态热传导问题的微分控制方程；

其中x,y,z为三个空间方向上的物理坐标，t(x,y,z)为温度响应，k(x,y,z)为热传导系数。

步骤二：由于制造工艺的限制、测量的误差以及环境的变化，此传热模型的结构热传导系数k1和k2、热流密度qs、环境温度te、表面换热系数h五个参数均含有一定的不确定性，且满足正态分布规律，引入五个(n＝5)随机变量ξii＝1,...,5表示这五个不确定输入参数，其均值和变异系数如表1所示，并记为向量的形式ξ＝(ξ1,ξ2,ξ3,ξ4,ξ5)＝(k1,k2,qs,te,h)。

表1传热模型随机不确定输入参数

于是步骤一中热传导问题的微分控制方程可改写为随机微分控制方程

步骤三：根据步骤二中随机变量的正态分布规律，选用埃尔米特正交多项式，将步骤二随机微分控制方程中涉及的温度响应t(x,y,z；ξ)进行近似表示，截断阶数设定为n＝3，得到随机温度响应的正交展开式

其中φi(ξ)为事先选定的埃尔米特正交多项式基底函数，ti(x,y,z)为对应的各项系数，多维指标i可表示为i＝(i1,i2,...,i5)且满足|i|＝i1+i2+...+i5，上述正交多项式中展开项的个数为

步骤四：设定配点水平，利用张量积法则和smolyak算法构造高维不确定空间的配点集合。首先，对于正态随机变量ξj而言，根据概率理论确定其主要分布区间其中ξj＝ej-3σj和表示下界和上界，ej和σj为随机变量ξj的均值和标准差。其次，设定配点水平k＝3，令l＝k+n＝8，则根据张量积法则和smolyak算法构造五维不确定空间的配点集合θ：

其中∪为并集运算的符号；ijj＝1,2,...,5表示第j个随机变量ξj在分布区间上的配点水平；表示第j个随机变量ξj对应配点水平ij在分布区间上的所有配点组成的集合，其配点数量和配点位置分别为：

其中和表示区间的中点和半径。

上述配点集合θ中的配点总数为m＝241，因此配点集合可具体表示为的形式，其中上标node表示配点。

步骤五：利用有限元程序计算步骤四配点集合中所有配点处的温度响应。首先，在配点处，步骤二中随机微分控制方程可具体表示为：

接着，利用软件nastran中的有限元程序对上述方程进行求解，可以得到步骤四配点集合θ中所有配点处的温度响应

步骤六：根据步骤五中所有配点处的温度响应建立步骤三随机温度响应正交展开式中各项系数ti(x,y,z)的线性方程组：

利用矩阵广义逆对此线性方程组进行求解，得到各项系数ti(x,y,z)的一组值。

步骤七：将步骤六中得到的各项系数ti(x,y,z)的一组值代回到步骤三随机温度响应正交展开式中，根据正交多项式基底函数φi(ξ)的正交关系，可以快速得到随机温度响应t(x,y,z；ξ)的均值e[t(x,y,z；ξ)]和标准差σ[t(x,y,z；ξ)]：

e[t(x,y,z；ξ)]≈e[tn(x,y,z；ξ)]＝t1(x,y,z)

四个观测点处随机温度响应的均值和标准差如表2和表3所示。与样本数为10⁷的传统蒙特卡洛抽样方法对比可以看出，本发明方法的计算误差小于10^-3，计算精度完全满足工程需求。另外，从计算时间上看，蒙特卡洛方法的计算时间为7870秒，本发明方法的计算时间仅为67秒，计算耗费远远小于蒙特卡洛方法。用本发明方法解决随机变量数大于等于5的高维随机热传导问题，计算精度高，计算耗费少，此功能是一般商用软件所不能实现的。

表2观测点处随机温度响应的均值

表3观测点处随机温度响应的标准差

以上所述的仅为本发明的较佳实施例而已，本发明不仅仅局限于上述实施例，凡在本发明的精神和原则之内所作的局部改动、等同替换、改进等均应包含在本发明的保护范围之内。