一种保持河道规模的临界流量计算方法与流程

本发明涉及一种保持河道规模的临界流量计算方法，是一种生态水文分析计算方法，是一种适用于枯水期河流生态安全，以保持河道规模对应河流生态水文条件为参考指标的计算方法。

背景技术：
生态水文季节的概念表明：河流生态系统一年内随水文情脉动，由汛前期、汛期、汛后枯水期构成一个完整的生理变化周期。每一个季节的生态保护目标不同。对于持续时间较长的汛后枯水期，河流处于低水流量，必须保持一种临界流量，以维持河流的一定规模，当流量小于这个数值时，河流将迅速消退直至干涸。保持河道规模的临界流量，其最基本的功能是要维持目标水体的基本形态，保证其成为一个连续体，并且以最小的水分条件，获得尽可能大的水域活动空间。本项技术主要适用于枯水季节的生态流量分析计算，与较为流行的计算最小生态流量分析方法不同之处在于：一是方法规范无计算者个人偏好，二是物理意义明确，计算出的临界流量有对应的河流规模物理参数支持。

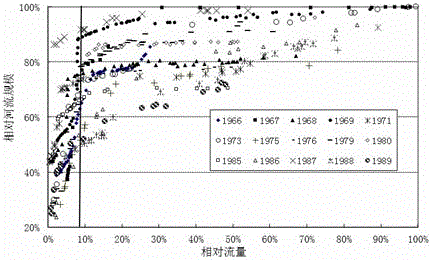
技术实现要素：
本发明提出了一种保持河道规模的临界流量计算方法。所述的方法通过水文观测记录数据，通过模型计算，在获取保持河道规模的临界流量的同时，还包含描述河道规模的物理参数。本发明的目的是这样实现的：一种保持河道规模的临界流量计算方法，其特征在于，所述的方法包括如下步骤：收集资料的步骤：用于收集至少一个河段观测站点的多年资料，包括：各种不同水文情势的流量及其对应的河流规模的数据；建立数值分析模型的步骤：用于首先设相对流量的初始值为q0，以相对流量的数值取整数为相对流量等步长：Δq=qi－qi－1等步长，其中：qi为断面流量系列中第i个流量，qi－1为第i－1个流量；则通过公式：计算各个与相对流量等步长Δq对应的各个相对河流规模平均值的变化量，其中：Δl为相对河流规模变化系列，为以Δq为步长时第i个相对河流规模变化；建立流量与规模曲线的步骤：用于以相对流量为横坐标，相对河流规模变化量为纵坐标，将q以Δq为步长变化时，其相对应的绘制相对流量和相对河流规模变化量的曲线；获取临界点的步骤：用于取相对河流规模变化量最大的点为保持河道临界流量的临界点E，E可表达为：E≈q0＋kmaxΔq，其中：kmax为最大处计算的步数；计算河流规模的步骤：用于通过公式计算与E对应的河流规模平均值LE：，其中：n为系列中的样本数，为正整数；计算动态变化范围的步骤：用于通过公式计算河流规模动态变化范围[B，A]：式中B为最小动态范围，A为最大动态范围，lj为与临界点对应的河流规模。本发明产生的有益效果是：本发明以多年平均流量和河流规模作为参照，针对低水情景（小于多年平均流量）进行无量纲处理，计算方法系统、规范，无个人偏好。可以方便地分析多沙河流和复杂断面，消除了个人偏好等主观因素的影响，成果客观性和适用性。所述计算方法物理过程与作用机制明确，临界流量包含了河流规模的物理参数，可为河流生态安全管理、保护、规划以及河道整治提供技术支撑。附图说明下面结合附图和实施例对本发明作进一步说明。图1是本发明的实施例所述q~l关系图；图2是本发明的实施例所述实际举例的利津站相对流量—河道规模关系图；图3是本发明的实施例所述实际举例的利津站相对流量—河道规模曲线的变化率曲线示意图。具体实施方式实施例：本实施例是一种保持河道规模的临界流量计算方法。本实施例所指临界流量，是以最少的水量保持河流尽可能大的规模。这是一种临界状态：当流量大于此临界流量时，河流规模没有显著变化；当流量小于此临界流量时，河流规模迅速衰减几近消失。因此临界流量可以认为是河道最小生态需水。河流生存条件由两类基本要素决定：一是水，没有水不成为河流，可以用水文学因素概括；二是河道空间特性，这些约束水的运动空间的条件，可以用形态学因素概括。临界流量取决于流量Q与河流规模L（河流规模可以是水面宽度或湿周）变化关系。建立无量纲的相对流量（q，低水流量占多年平均流量比重Qi/）和河流相对规模（，低水流量时的河流规模占平均河流规模比重Li/）的变化关系。通过对长系列多相位的河道（大断面观测资料）、水位流量关系等实测水文资料进行计算分析，绘制出相对流量—相对河道规模即q-l关系图，集中进行综合分析，如图1。大量的计算点据显示，在相对流量E处，相对流量－相对河道规模关系出现明显转折。尽管由于河道冲淤，各不同年份转折点对应的河道规模有所不同（变化范围在A和B之间），但相对流量基本不变。因此，可以判定流量E处是河流生存的临界点，当流量大于E时，河流规模变化不大，而当流量小于E时，河流规模迅速衰减，直至消失。由此，确定E为该断面的保持河道规模稳定的临界点：Qmin=E。其对应河流规模在A和B之间。对以上内容进行数学描述。观察q-l曲线，在临界流量E左右，即曲线斜率即其一阶导数发生剧变，求曲线一阶导数，则有：（1）在E左右发生剧变：，流量E处曲线斜率最大，则其二阶导数等于零，也即：（2）在实际中以数值分析处理找到q-l关系曲线，利用河流大断面观测水文资料进行数值分析，通过差分插值求解导数，计算临界流量。对于实测河流，以n年资料，建立数值模拟模型。采用数值插值差分，式（1）变为：（3）对n年求和平均：（4）近似处理为：（5）设q初始值为q0取Δq=qi－qi－1等步长，其中：qi为断面流量系列中第i个流量，qi－1为第i－1个流量。上式简化为：（6）利用式（6）进行计算，点绘关系曲线。其顶点处i=kmax，此时q=E，或：E≈q0＋kmaxΔq（7）E对应的河流平均规模LE：（8）其变化范围[B，A]：（9）根据以上描述，本实施例所述的方法的具体步骤如下：收集资料的步骤：用于收集至少一个河段观测站点的多年河段资料，包括：各年的流量和河流规模的数值；建立数值模拟模型的步骤：用于首先设相对流量的初始值为q0，以相对流量的数值取整数为相对流量等步长：Δq=qi－qi－1等步长，则通过公式：计算各个与相对流量等步长Δq对应的各个相对河流规模平均值的变化量，其中：Δl为相对河流规模变化系列，为以Δq为步长时第i个相对河流规模变化；建立流量与规模曲线的步骤：用于以相对流量为横坐标，相对河流规模变化为纵坐标，将q，及相对应的绘制曲线；获取临界点的步骤：用于取关系曲线中相对河流规模变化量最大的点为保持河道临界流量的临界点E，E可表达为：E≈q0＋kmaxΔq，其中：kmax为相对河流规模变化量最大处计算的步数。计算河流规模的步骤：用于通过公式计算与E对应的河流规模平均值LE：，其中：n为系列中的样本数，为正整数。计算动态变化范围为的步骤：用于通过公式计算河流规模动态变化范围[B，A]：式中B为最小动态范围，A为最大动态范围，lj为与临界点对于的河流规模。实际举例：利津站是黄河最下游的一个水文站，位于山东省东营市利津县利津镇刘家夹河村，距离黄河入海口104km，控制断面泥沙多，冲淤严重。以利津站资料为例，说明临界流量计算过程。（1）相对流量～相对河道规模关系图采用1966~1989年利津站资料，绘制低水期利津站相对流量～相对河道规模关系图，见图2。从图中可以看出，虽然利津站冲淤频繁，但在相对流量约9.0%处，相对流量～相对河流规模关系出现明显转折。因此确定利津站保持河道规模的临界流量百分比为9.0%，相应的临界流量为166m3/s。不同年份临界流量维持的河流规模范围为40.0％～91.8%。（2）计算临界流量采用1966~1989年利津站资料，取初始点=1（即多年平均径流量的1%），步长Δq=0.1。利用式（6）进行计算，点绘利津站相对河流规模与相对流量曲变化量线一阶导数变化，见图3。kmax=73时，相对流量的变化量最大，因此E=q0+kmaxΔq=8.3。由此确定利津站临界相对流量为8.3%。利津多年平均流量为1840m3/s，因此，利津站最小生态流量为153m3/s。以式（8）、（9）计算对应的河流规模为68%，变化范围50%~86%。最后应说明的是，以上仅用以说明本发明的技术方案而非限制，尽管参照较佳布置方案对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案（比如曲线的拟合方式、E的求解方式等）进行修改或者等同替换，而不脱离本发明技术方案的精神和范围。