一种非轴对称元件的二维数值计算方法与流程

本发明涉及空气系统二维数值模拟方法，尤其涉及一种非轴对称元件的二维数值计算方法。

背景技术：

燃气轮机的空气系统流路中元件丰富，流路复杂，能够直接开展整机空气系统三维数值的计算机价格昂贵难度较大，目前开展流路层面的计算分析手段主要是一维流路计算配合局部的二维/三维计算，一维计算的效率高但简化处理较多，对内部流动细节反映不足，而局部二维/三维模拟获得的细节丰富但计算效率低，且不能反映空气系统全局，这些方法的适用范围受到限制，计算结果的参考价值有限。由于处理非对称元件的技术存在欠缺，限制了二维CFD(Computational Fluid Dynamics,计算流体力学)技术在燃气轮机空气系统领域的应用。

在空气系统中有大量旋转的元件或结构，这类元件或结构通过运动对流经其间的空气起作用。从结构上看有完全关于发动机转轴对称的元件，如盘腔、中心通气管等；也有关于转轴不对称的元件，如与发动机轴线不同轴的孔、喷嘴、缝隙等。将轴对称元件按等面积原则简化为二维模型时误差较小，但非轴对称元件在二维数值模拟时则丢失元件对流体的作用以及周向流动信息。因此简单的二维化数值模拟应用到发动机空气系统时会带来一系列问题，比如，旋转的流通元件处于旋转态或元件所处环境为强旋流，此时采用前述方法模拟会丢失大量的流动信息，如预旋喷嘴出口气流的强烈周向旋转，气流过孔时气流与静止/旋转孔之间的相互作用等。对这类场合的非对称元件做简单简化将带来较大误差。

技术实现要素：

本发明提供一种非轴对称元件的二维数值计算方法，解决非轴对称元件在二维数值模拟时丢失元件对流体的作用以及周向流动信息造成的较大模拟误差的问题，提高空气系统二维模拟的准确性和实用性。

为实现以上目的，本发明提供以下技术方案：

一种非轴对称元件的二维数值计算方法，包括以下步骤：

根据非轴对称元件的物理模型简化所述物理模型；

根据所述物理模型的类型建立二维计算模型，确定计算域的范围，并根据所述计算域划分网格；

根据所述物理模型的类型建立周向速度比模型，确定流体域的范围，并计算所述流体域的周向速度比和虚转速所述周向速度比表征所述非轴对称元件前后的周向速度变化量，所述虚转速表征所述非轴对称元件对流场的作用；

根据所述网格和所述虚转速计算出元件进口速度向量V_i，如果所述元件进口速度向量V_i-V_i-1的差值小于设定阈值V₀，则所述二维数值计算完成，否则返回计算所述虚转速

优选的，所述根据非轴对称元件的物理模型简化所述物理模型包括：

按等流通面积原则简化流通区域；

去除非轴对称元件对流动影响不大的边角、退刀槽；

简化非轴对称元件的垫片、锁片、配重；

合并相邻具有相同运动特征的结构。

优选的，所述根据所述物理模型的类型建立二维计算模型，确定计算域的范围，并根据所述计算域划分网格，包括：

确定孔类或凸起类的模型处理方法；

对互相冲突的非轴对称元件进行折中。

优选的，所述根据所述物理模型的类型建立周向速度比模型，包括：孔类周向速度比模型和凸起类周向速度比模型。

优选的，所述周向速度变化量为周向速度比C_V，其中C_v＝V_2,θ/V_1,θ，V_2,θ为进口处气流的平均周向速度，V_1,θ为出口处气流的平均周向速度。

优选的，周向速度比C_V为

$C_v=\frac{{\mathrm{Sr}}_2}{{\mathrm{Sr}}_1}=\frac{{\mathrm{Sr}}_1(A_{cross}/A)+1(1-A_{cross}/A)}{{\mathrm{Sr}}_1}$

其中，l为孔的厚度，d为孔径，α为进口气流与孔轴线夹角，β为径向夹角，γ临界角度，A为孔的面积，A_cross为孔的流通直通面积，Sr₁、Sr₂为旋流比。

优选的，所述虚转速包括孔类元件的虚转速和凸起类元件的虚转速；

所述孔类元件的虚转速ω¹＝(C_v-1)V_1,θ/r₂，其中，V_1,θ为进口周向速度，r₂为出口径向位置；

所述凸起类元件的虚转速为

其中，V_1,θ为凸起元件进口周向速度，r为凸起元件旋转半径，d为凸起元件当量直径，ω'为旋转系的转速。

本发明提供一种非轴对称元件的二维数值计算方法，通过对非轴对称元件设置虚旋转的方法，获得一个虚转速，使非轴对换元件对流场的作用和真实流动相同。解决非轴对称元件在二维数值模拟时丢失元件对流体的作用以及周向流动信息造成的很大模拟误差的问题，提高空气系统二维模拟的准确性和实用性。

附图说明

为了更清楚地说明本发明的具体实施例，下面将对实施例中所需要使用的附图作简单地介绍。

图1：是本发明提供的一种非轴对称元件的二维数值计算方法流程图；

图2：是本发明实施例提供的一种基于虚旋转方法的二维CFD分析流程图；

图3：本发明实施例提供的孔模型示意图；

图4：是本发明实施例提供的一种盘结构及其气流流路示意图；

图5：是本发明实施例提供的盘结构凸起流线对比示意图；

图6：是本发明实施例提供的盘结构压力等值线对比示意图；

图7：是本发明实施例提供的盘结构周向速度等值线对比示意图。

具体实施方式

为了使本技术领域的人员更好地理解本发明实施例的方案，下面结合附图和实施方式对本发明实施例作进一步的详细说明。

针对当前二维CFD技术在对非对称元件存在忽略其周向流动的作用，易使二维数值模拟与真实流动造成很大的误差，本发明提供一种非轴对称元件的二维数值计算方法，通过对非轴对称元件设置虚旋转的方法，获得一个虚转速，使非轴对换元件对流场的作用和真实流动相同。解决非轴对称元件在二维数值模拟时丢失元件对流体的作用以及周向流动信息造成的很大模拟误差的问题，提高空气系统二维模拟的准确性和实用性。

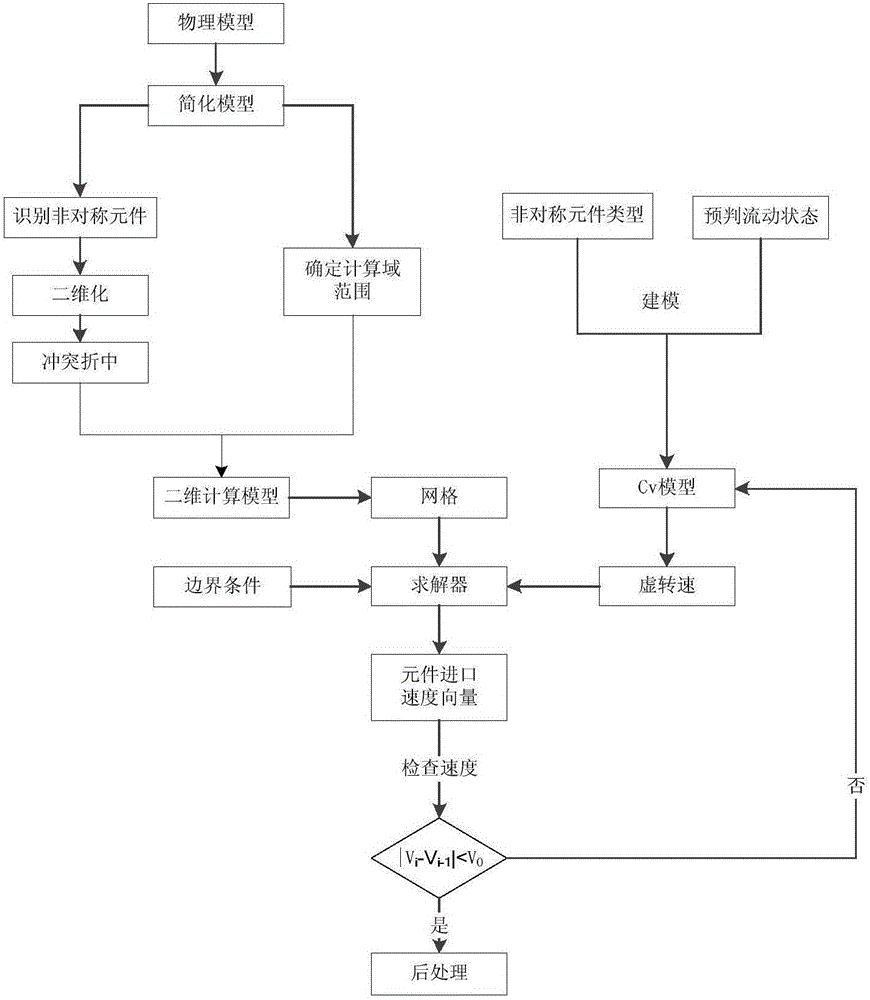
如图1所示，为本发明提供的一种非辆对称元件的二维数值计算方法流程图，包括以下步骤：

S1：根据非轴对称元件的物理模型简化所述物理模型；

S2：根据所述物理模型的类型建立二维计算模型，确定计算域的范围，并根据所述计算域划分网格；

S3：根据所述物理模型的类型建立周向速度比模型，确定流体域的范围，并计算所述流体域的周向速度比和虚转速所述周向速度比表征所述非轴对称元件前后的周向速度变化量，所述虚转速表征所述非轴对称元件对流场的作用；

S4：根据所述网格和所述虚转速计算出元件进口速度向量V_i，如果所述元件进口速度向量V_i与其上一次的值V_i-1的差值小于设定阈值V₀，则所述二维数值计算完成，否则重新计算所述周向速度比。

具体地，如图2所示，为本发明实施例提供的一种基于虚旋转方法的二维CFD分析流程图，包括以下步骤：

S11：输入物理模型本流程的输入为研究对象的物理模型和边界条件，计算目的为获得研究对象的周向速度分布、腔压分布等流场信息；

S12：简化模型对研究对象的CAD图纸或物理模型，其做模型清理和简化，去除对流动影响不大的边角、退刀槽等，简化垫片、锁片、配重等，合并相邻或具有相同运动特征的结构，获得简化模型；

S13：识别非对称元件分析物理模型的流路，确认模型内各个元件的结构参数和运动信息，区分对称元件和非轴对称元件，识别非轴对称元件的类型和运动形态；

S14：二维化在S13之后确立各个非轴对称元件的二维化原则和方法；根据需求和对计算结果的影响确定计算域的范围；

S15：建立二维模型在S14之后依据确定的原则对非轴对称元件做平面化处理，在该过程中互相冲突的非轴对称元件应根据各自的影响做折中，而后融入整个流路计算域，建立二维计算模型；按数值模拟的要求对计算域做网格划分；

S16：网格导入在S15之后将网格导入求解器，设置边界条件，按常规方法完成首次计算；

S17：建立周向速度比模型在S13识别出非轴对称元件后整理被识别的非轴对称元件类型，对每个非轴对称元件预判流动状态，据此建立周向速度比模型；

S18：计算虚转速在S17之后，读取各非轴对称元件进口速度分量，根据进口的速度分量计算周向速度比，而后计算该元件在该状态的虚转速；将虚转速赋给各个非轴对称元件，在求解器中计算至满足收敛判据；

S19：检查本轮CFD计算的非轴对称元件进口速度和上轮计算的差值，若差值小于指定值，停止计算。进行后处理。否则返回第S17步骤。

进一步，所述根据非轴对称元件的物理模型简化所述物理模型包括：

步骤一：去除非轴对称元件对流动影响不大的边角、退刀槽；

步骤二：简化非轴对称元件的垫片、锁片、配重；

步骤三：合并相邻具有相同运动特征的结构。

同时，所述根据所述物理模型的类型建立二维计算模型，确定计算域的范围，并根据所述计算域划分网格，包括：确定孔类或凸起类的模型处理方法和对互相冲突的非轴对称元件进行折中。

进一步，所述根据所述物理模型的类型建立周向速度比模型，包括：孔类周向速度比模型和凸起类周向速度比模型。

周向速度变化量由周向速度比C_V表征，其中C_v＝V_2,θ/V_1,θ，V_2,θ为进口处气流的平均周向速度，V_1,θ为出口处气流的平均周向速度。

周向速度比C_V为

其中，

a<γ且β<γ

l为孔的厚度，d为孔径，α为进口气流与孔轴线夹角，β为径向夹角，γ临界角度，A为孔的面积，A_cross为孔的流通直通面积，Sr₁、Sr₂为旋流比。可参考图3所示，为本发明实施例提供的孔模型示意图。

进一步，所述虚转速包括孔类元件的虚转速和凸起类元件的虚转速；所述孔类元件的虚转速ω₁＝(C_v-1)V_1,θ/r₂，其中，V_1,θ为进口周向速度，r₂为出口径向位置；所述凸起类元件的虚转速，其中，V_1,θ为凸起元件进口周向速度，r为凸起元件旋转半径，d为凸起元件当量直径，ω'为旋转系的转速。

在实际应用中，如图4所示，为本发明实施例提供的一种盘结构及其气流流路示意图，该盘结构的空腔即为空气流路，气流从下方进入盘腔，从孔流出，盘腔内有螺栓，盘1、2处于旋转状态，其中螺栓和孔为模型内的两个非轴对称元件。气流进入盘腔后一部分向外直接穿过孔流出，另一部分需要流经螺栓之间的空间，而后经孔流出，即螺栓间的区域实质上也是气流通道，经该非对称轴元件的二维数值计算方法可获得如图5、图6、图7所示的效果，图5为本发明实施例提供的盘结构凸起流线对比示意图，图6为本发明实施例提供的盘结构压力等值线对比示意图，从图6上可见，常规方法计算的结果显示在低半径压力损失较大，上方腔压有一定恢复，采用本申请所述方法计算，低半径损失较小，上方腔压随半径增大而增大，与实际流动现象一致，下方盘腔内由于凸起物搅拌造成的压力等值线密集，压力梯度比常规方法的更大。图7为本发明实施例提供的盘结构周向速度等值线对比示意图，从常规方法的模拟结果中可见，气流穿过旋转孔前后的周向速度变化很小，等值线呈纵向排列，从本申请的计算方法结果中则观察到，气流穿过旋转孔前后周向速度有明显变化，等值线形态和常规方法结果显著不同。采用虚旋转方法也获得了凸起元件位置的周向速度分布。

可见，本发明提供一种非轴对称元件的二维数值计算方法，通过对非轴对称元件设置虚旋转的方法，获得一个虚转速，使非轴对换元件对流场的作用和真实流动相同。解决非轴对称元件在二维数值模拟时丢失元件对流体的作用以及周向流动信息造成的很大模拟误差的问题，提高空气系统二维模拟的准确性和实用性。

以上依据图示所示的实施例详细说明了本发明的构造、特征及作用效果，以上所述仅为本发明的较佳实施例，但本发明不以图面所示限定实施范围，凡是依照本发明的构想所作的改变，或修改为等同变化的等效实施例，仍未超出说明书与图示所涵盖的精神时，均应在本发明的保护范围内。