一种基于挠度影响线的桥梁局部损伤量化方法与流程

本发明涉及工程结构健康监测领域，具体是涉及结构健康监测系统下一种基于挠度影响线的桥梁局部损伤量化方法。
背景技术：
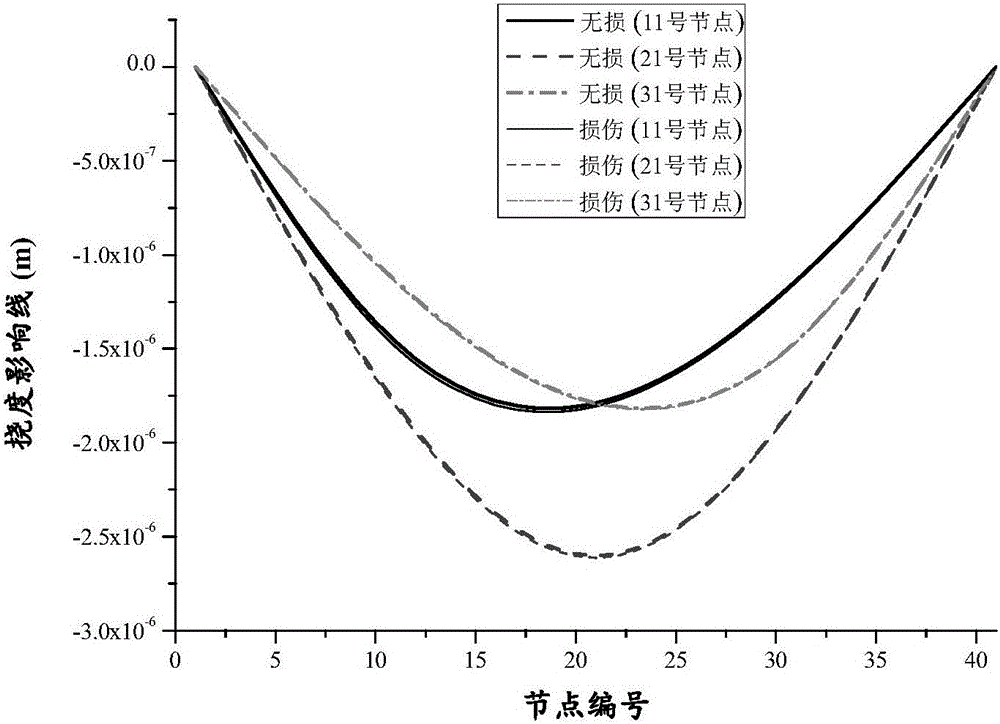
：在过去的几十年内，中国修建了大量的桥梁，其中不乏跨径达千米级的大跨桥梁。考虑到环境腐蚀、材料老化、荷载的长期与疲劳效应，以及台风、地震等突发灾难的影响，桥梁建成伊始便伴随结构劣化。损伤始于局部，但桥梁局部损伤往往不会造成结构整体特性的显著改变，这给损伤识别带来了很大的困难。结构损伤识别通常是指检测结构构件刚度的减少。Rytter将损伤识别分为4个层次：(1)确定结构中是否存在损伤；(2)确定损伤的位置；(3)对损伤程度进行量化；(4)预测结构的剩余使用寿命[1]。判定损伤是否发生是损伤识别的基础，损伤定位是核心，损伤程度量化及剩余寿命预测则是损伤识别的终极目标，现阶段大多数损伤识别方法无法达到该层次。近年来，有学者致力于研究基于静力特性的损伤指标，基于桥梁影响线构造损伤指标就是其中很有代表性的一种。Zaurin和Catbas[2]就提出影响线会是一个良好的损伤指标，并通过实验室试验进行损伤识别验证。Chen等[3]基于影响线变化的一次差分指标，较好地进行了定位了大跨悬索桥模型上模拟的损伤。Sun等[4]也提出类似于坐标模态置信度法的影响线损伤指标。上述基于影响线损伤识别的文献都仅仅做到了判断损伤或损伤定位，没有实现损伤程度的量化。目前，较为成功的损伤量化方法是基于模型更新的方法。模型更新方法主要包括直接法和灵敏度修正法。直接法是直接修正结构的系统矩阵(主要指质量、刚度和阻尼矩阵)，使得数值模拟与实测结果相符。一般的做法，如文献[5]假设结构的质量矩阵是准确的，进而基于结构的特征向量修正刚度矩阵。但该方法的局限性就是，更新后的系统矩阵会失去原先的物理意义，同时单元节点之间的连续性也无法得到保证[6]。基于灵敏度是另一类方法，是通过建立目标函数表示物理系统响应的解析解和试验值之间的差异，再通过优化算法最小化该差异，常用于参数识别和损伤识别。在损伤识别方面，在Fritzen等[7]1998年一篇文献中，就尝试通过灵敏度的模型更新方法进行损伤识别，基于无损的结构模型和对损伤的描述数据进行损伤定位及程度量化。Teughel等[8]提出了通过特征频率及模态的迭代进行敏感性模型更新，根据更新结果和损伤函数量化损伤。进一步，Fang等[9]将Teughel所提出的一维损伤函数扩展成了二维函数，用以修正平面有限元模型，并在实验室做了验证。基于灵敏度的模型更新方法进行损伤量化的研究，虽然已取得了一些成果，但也仍旧存在不足。例如，(1)灵敏度矩阵的构造往往存在困难，并且容易出现迭代不收敛的情况；(2)优化迭代过程计算量大，修正效率得不到提高。参考文献：[1]RytterA.Vibrationbasedinspectionofcivilengineeringstructures[D].AalborgUniversity,Copenhagen,Denmark,1993.[2]ZaurinR,CatbasFN.Structuralhealthmonitoringusingvideostream,influencelines,andstatisticalanalysis[J].StructuralHealthMonitoring,2011,10(3):309-332.[3]ChenZW,ZhuS,XuYL,LiQandCaiQL.Damagedetectioninlongsuspensionbridgesusingstressinfluencelines[J].JournalofBridgeEngineering,2015,20(3):05014013.[4]SunS,SunLandChenL.DamageDetectionBasedonStructuralResponsesInducedbyTrafficLoad:MethodologyandApplication[J].InternationalJournalofStructuralStabilityandDynamics,2015:1640026.[5]BaruchM.Optimizationproceduretocorrectstiffnessandflexibilitymatricesusingvibrationtests[J].AIAAjournal,1978,16(11):1208-1210.[6]FriswellM,MottersheadJE.Finiteelementmodelupdatinginstructuraldynamics[M].SpringerScience&BusinessMedia,1995.[7]FritzenCP,JenneweinDandKieferT.Damagedetectionbasedonmodelupdatingmethods[J].MechanicalSystemsandSignalProcessing,1998,12(1):163-186.[8]TeughelsA,MaeckJandDeRoeckG.DamageassessmentbyFEmodelupdatingusingdamagefunctions[J].Computers&structures,2002,80(25):1869-1879.[9]FangSE,PereraRandDeRoeckG.Damageidentificationofareinforcedconcreteframebyfiniteelementmodelupdatingusingdamageparameterization[J].JournalofSoundandVibration,2008,313(3):544-559.技术实现要素：本发明要解决的技术问题是提供一种基于挠度影响线的桥梁局部损伤量化方法。本发明包括以下步骤：1)刚度矩阵的特征值分解与组合：当单元刚度矩阵Ki不满秩时，假设Ki的秩为r，则单元刚度矩阵的特征值分解可表示为：Ki=UiΛiUiT=Σj=1rσijuij(uij)T---(1)]]>式中，是Ki的第j个特征值，是对应的特征向量，Λi和Ui分别是特征值矩阵和特征向量矩阵，令qij=σijuij---(2)]]>ci=[qi1,qi2,...qir]---(3)]]>式中，和ci分别定义为第i个单元的刚度连接向量和刚度连接矩阵，维数分别为n×1和n×r，n为自由度数，则Ki还可表示为：Ki=ciciT---(4)]]>整体刚度矩阵可通过整体坐标系下单元刚度矩阵的叠加得到：K=Σi=1NKi---(5)]]>其中，N是单元数，并且单元刚度矩阵Ki与整体刚度矩阵K的维数保持一致，将式(4)代入(5)中，则整体刚度矩阵可表达为：K=Σi=1Nγi·ciciT---(6)]]>或K＝CPCT(7)式中，C＝[c1c2,…,cN]定义为整体刚度连接矩阵，其维数为n×s，其中s＝r×N；γi表示第i个单元的损伤参数，γi＝1则为无损，0＜γi＜1则表示存在某种程度的损伤，P是损伤识别矩阵，维数为s×s；若无损，则P为单位矩阵；若某单元出现损伤，则矩阵对角线上的对应值不为1；2)影响线矩阵的构造：从结构的整体刚度矩阵K和柔度矩阵F的物理意义出发，有如下表达式：KF＝I(8)式中，I为单位阵；由式(7)和式(8)，可重新构造柔度矩阵如下：F＝(C-1)TP-1C-1(9)令B＝P-1,D＝(C-1)T则F＝DBDT(10)式中，D是C矩阵虚拟逆的转置，定义为整体柔度连接矩阵，其维数与C一致；根据挠度影响线的定义，移动的竖向单位力仅作用在单元竖向位移自由度上，引入荷载输入自由度选择矩阵Q(维数n×m，n为自由度数，m表示竖向位移自由度个数)，如下所示：矩阵Q中相应的行与列上的数值为1，则表示该自由度被选中施加单位力/力矩荷载；若为0，则表示未被选中；式(10)右乘矩阵Q得：FQ＝DBDTQ(12)另外，考虑到实际情况，无法也无必要输出所有自由度的响应，故选择性地输出其中部分自由度的响应；定义响应输出自由度选择矩阵S(维数为l×n，l表示输出的挠度自由度个数)如下所示：S=0...10...0...0...00...0...10...0...00.........10...0---(13)]]>矩阵S中相应的行与列上的数值为1，则表示该自由度被选中输出响应；若为0，则表示未被选中，式(12)左乘矩阵S可得：SFQ＝SDBDTQ(14)从影响线的定义可知，上式可表示特定响应输出自由度的挠度影响线矩阵DIL，而DIL其实是柔度矩阵的一部分，通过选择荷载输入自由度和响应输出自由度，如下式可将柔度矩阵转化为挠度影响线矩DIL：DIL＝SFQ(15)3)损伤程度的量化：若待检测结构出现损伤，用ΔK和ΔF表示损伤所引起的整体刚度矩阵和整体柔度矩阵的变化量，将损伤前后的整体刚度矩阵和柔度矩阵表示为增量形式：Fd＝Fu+ΔF(16)Kd＝Ku-ΔK(17)其中，刚度矩阵K和柔度矩阵F的下标u表示无损状态，d则表示损伤状态；由式(5)可知，整体刚度矩阵的增量ΔK可表示为在同一坐标系下的单元刚度矩阵的增量和，即：ΔK=Σi=1NαiΔKi---(18)]]>其中Ki是第i号单元的单元刚度矩阵的增量，αi是第i号单元的健康系数(0≤αi≤1)；αi＝0表示无损，αi＝1表示全部损伤；由公式(6)、(7)和(18)可得：Kd=Σi=1N(1-αi)ciciT---(19)]]>则ΔK＝Ku-Kd＝CΔPCT(20)其中，ΔP是由αi(i＝1,…,N)所组成的斜对角矩阵，可表示为：相应地，柔度矩阵的变化量可表示为：ΔF＝DΔBDT(22)相似于ΔP矩阵的推导，矩阵ΔB可表达为：其中，由式(15)和式(22)可得损伤前后的影响线变化量ΔZ：ΔZ＝DILu-DILd＝S(Fu-Fd)Q＝SΔFQ＝SDBDTQ(24)式中，DILu和DILd分别表示所选择自由度在损伤前后的挠度影响线。令L＝SD,R＝DTQ，式(24)可以重写成：ΔZ＝LΔBR(25)矩阵L,ΔB,R,ΔZ的维数分别为l×s、s×s、s×m和l×m，具体形式如下：L=a1,1a1,2...a1,sa2,1a2,2...a2,s............al,1al,2...al,s,R=b1,1b1,2...b1,mb2,1b2,2...b2,m............bs,1bs,2...bs,m,ΔZ=d1,1d1,2...d1,md2,1d2,2...d2,m............dl,1dl,2...dl,m---(26-28)]]>整理矩阵运算结果，可得如下表达式：dij=Σk=1sλkai,kbk,j---(29)]]>还可写成矩阵的形式：a1,1b1,1a1,2b2,1...a1,sbs,1............ai,1b1,jai,2b2,j...ai,sbs,j............al,1b1,mal,2b2,m...al,sbs,mλ1...λk...λs=d1,1...di,j...ds,m---(30)]]>其中，定义为柔度系数矩阵。若定义第e列的柔度系数矩阵：则式(30)可改写为：λk(k＝1,…,s,且s＝r×N)是反映单元k损伤的系数，N是单元数，r是单元刚度矩阵的秩；在多数情况下，单元刚度矩阵的秩大于1，于是出现r≥N的情况，即多个损伤系数对应于同一个单元；为此，采用了类似矩阵压缩的方法，经处理后，式(32)可表示为：θ1...θi...θNβ1...βi...βN=d1,1...di,j...dl,m---(33)]]>其中，在矩阵[θ1…θi…θN]和[d1,1…di，j…dl,m]T已知的前提下，可通过公式(33)反求第i号单元的损伤系数βi(i＝1,…,N)；对于这样一个逆问题求解，采用有约束的最小二乘法求解法，即在考虑残差最小二乘解最小的基础上，还要求待识别的单元损伤系数βi落在[0,1]的区间范围内。本发明基于刚度矩阵特征分解构造影响线矩阵，建立损伤参数与影响线变化之间的联系，进而提出基于挠度影响线的损伤量化方法。本发明通过特征参数分解的方法利用影响线对损伤进行量化，获得类似灵敏度的矩阵更方便，求解过程可不迭代，求解速度更快。本发明基于桥梁挠度影响线，可实现对局部损伤定位的同时，更能准确量化损伤程度。与现有技术相比，本发明具有以下的主要优点：一、同现有的损伤指标相比，基于影响线的损伤指标对桥梁局部损伤更敏感，而对环境因素变化不敏感，较适用于在运营环境下检测桥梁的局部损伤。二、相比传统基于灵敏度矩阵的损伤定位方法，类似灵敏度矩阵的构造更加简单方便，求解过程可不迭代，避免了数值求解的迭代不收敛问题，并且提高了求解速度。附图说明图1为简支梁示意图。图2为单处损伤前后的挠度影响线。图3为单处损伤的挠度影响线变化。图4为基于单条影响线的损伤程度识别结果：损伤工况一。图5为基于多条影响线的损伤程度识别结果：损伤工况一。图6为多处损伤前后的挠度影响线。图7为多处损伤前后的挠度影响线。图8为基于多条影响线的损伤程度识别结果：损伤工况二。图9为连续梁示意图。图10为基于多条影响线的损伤程度识别结果：连续梁损伤工况。图11为实验室的简支铝梁示意图。图12为损伤阶段的实验室梁示意图。图13为模型更新输出响应与实测响应对比。图14为不同位置的挠度影响线变化：实验室损伤工况一。图15为基于单条影响线的损伤程度识别结果：实验室损伤工况一。图16为基于多条影响线的损伤程度识别结果：实验室损伤工况一。图17为基于不同数量影响线的损伤程度识别结果：实验室损伤工况二。在图1、9、11和12中，标记A为移动力。具体实施方式下面结合附图和实施例对本发明做进一步的详细说明。本发明提出结构健康监测系统下基于影响线的桥梁局部损伤识别方法，主要包括以下几个步骤：步骤1，刚度矩阵的分解与组合在大多数情况下，单元刚度矩阵Ki都不是满秩的。假设Ki的秩为r，则单元刚度矩阵的特征值分解可表示：Ki=UiΛiUiT=Σj=1rσijuij(uij)T---(1)]]>式中，是Ki的第j个特征值，是对应的特征向量。Λi和Ui分别是特征值矩阵和特征向量矩阵。令qij=σijuij---(2)]]>ci=[qi1,qi2,...qir]---(3)]]>式中，和ci分别定义为第i个单元的刚度连接向量和刚度连接矩阵，维数分别为n×1和n×r，n为自由度数。则Ki还可表示为：Ki=ciciT---(4)]]>众所周知，整体刚度矩阵可通过整体坐标系下单元刚度矩阵的叠加得到：K=Σi=1NKi---(5)]]>其中，N是单元数，并且单元刚度矩阵Ki与整体刚度矩阵K的维数保持一致。将式(4)代入(5)中，则整体刚度矩阵可表达:K=Σi=1Nγi·ciciT---(6)]]>或K＝CPCT(7)式中，C＝[c1c2,…,cN]定义为整体刚度连接矩阵，其维数为n×s，其中s＝r×N。γi表示第i个单元的损伤参数，γi＝1则为无损，0＜γi＜1则表示存在某种程度的损伤。P是损伤识别矩阵，维数为s×s。若无损，P为单位矩阵；若某单元出现损伤，则矩阵对角线上的对应值不为1。步骤2，影响线矩阵的构造从结构的整体刚度矩阵K和柔度矩阵F的物理意义出发，可如下表达式：KF＝I(8)式中，I为单位阵。由式(7)和式(8)，可重新构造柔度矩阵如下：F＝(C-1)TP-1C-1(9)令B＝P-1,D＝(C-1)T则F＝DBDT(10)式中，D是C矩阵虚拟逆的转置，定义为整体柔度连接矩阵，其维数与C一致。根据挠度影响线的定义，移动的竖向单位力仅作用在单元竖向位移自由度上。引入荷载输入自由度选择矩阵Q(维数n×m，m表示竖向位移自由度个数)，如下所示：矩阵Q中相应的行与列上的数值为1，则表示该自由度被选中施加单位力/力矩荷载；若为0，则表示未被选中。式(10)右乘矩阵Q得：FQ＝DBDTQ(12)另外，考虑到实际情况，无法也无必要输出所有自由度的响应，故选择性地输出其中部分自由度的响应。定义响应输出自由度选择矩阵S(维数为l×n，l表示输出的挠度自由度个数)如下所示：S=0...10...0...0...00...0...10...0...00.........10...0---(13)]]>矩阵S中相应的行与列上的数值为1，则表示该自由度被选中输出响应；若为0，则表示未被选中。式(12)左乘矩阵S可得：SFQ＝SDBDTQ(14)从影响线的定义可知，上式可表示特定响应输出自由度的挠度影响线矩阵DIL，而DIL其实是柔度矩阵的一部分。通过选择荷载输入自由度和响应输出自由度，如下式可将柔度矩阵转化为挠度影响线矩DIL。DIL＝SFQ(15)步骤3，损伤程度的量化若待检测结构出现损伤，用ΔK和ΔF表示损伤所引起的整体刚度矩阵和整体柔度矩阵的变化量。将损伤前后的整体刚度矩阵和柔度矩阵表示为增量形式：Fd＝Fu+ΔF(16)Kd＝Ku-ΔK(17)其中，下标u表示无损状态，相应的d表示损伤状态。由式(5)可知，整体刚度矩阵的增量ΔK可表示为在同一坐标系下的单元刚度矩阵的增量和，即：ΔK=Σi=1NαiΔKi---(18)]]>其中Ki是第i号单元的单元刚度矩阵的增量，αi是第i号单元的健康系数(0≤αi≤1)。αi＝0表示无损，αi＝1表示全部损伤。由公式(6)、(7)和(18)可得：Kd=Σi=1N(1-αi)ciciT---(19)]]>则ΔK＝Ku-Kd＝CΔPCT(20)其中，ΔP是由αi(i＝1,…,N)所组成的斜对角矩阵，可表示为：相应地，柔度矩阵的变化量可表示为：ΔF＝DΔBDT(22)相似于ΔP矩阵的推导，矩阵ΔB可表达为：其中，由式(15)和式(22)可得损伤前后的影响线变化量ΔZ：ΔZ＝DILu-DILd＝S(Fu-Fd)Q＝SΔFQ＝SDBDTQ(24)式中，DILu和DILd分别表示所选择自由度在损伤前后的挠度影响线。令L＝SD,R＝DTQ，式(24)可以重写成：ΔZ＝LΔBR(25)矩阵L,ΔB,R,ΔZ的维数分别为l×s、s×s、s×m和l×m，具体形式如下：L=a1,1a1,2...a1,sa2,1a2,2...a2,s............al,1al,2...al,s,R=b1,1b1,2...b1,mb2,1b2,2...b2,m............bs,1bs,2...bs,m,ΔZ=d1,1d1,2...d1,md2,1d2,2...d2,m............dl,1dl,2...dl,m---(26-28)]]>整理矩阵运算结果，可得如下表达式：dij=Σk=1sλkai,kbk,j---(29)]]>还可写成矩阵的形式：a1,1b1,1a1,2b2,1...a1,sbs,1............ai,1b1,jai,2b2,j...ai,sbs,j............al,1b1,mal,2b2,m...al,sbs,mλ1...λk...λs=d1,1...di,j...ds,m---(30)]]>其中，定义为柔度系数矩阵。若定义第e列的柔度系数矩阵：则式(30)可改写为：λk(k＝1,…,s,且s＝r×N)是反映单元k损伤的系数，N是单元数，r是单元刚度矩阵的秩。在多数情况下，单元刚度矩阵的秩大于1，于是出现r≥N的情况，即多个损伤系数对应于同一个单元。为此，采用了类似矩阵压缩的方法，经处理后，式(32)可表示为：θ1...θi...θNβ1...βi...βN=d1,1...di,j...dl,m---(33)]]>其中，在矩阵[θ1…θi…θN]和[d1,1…di，j…dl,m]T已知的前提下，可通过公式(33)反求第i号单元的损伤系数βi(i＝1,…,N)。对于这样一个逆问题求解，本文采用了有约束的最小二乘法求解法，即在考虑残差最小二乘解最小的基础上，还要求待识别的单元损伤系数βi落在[0,1]的区间范围内。以下给出具体实施例：实施例1：简支梁及连续梁数值模型损伤量化简支梁模型设计尺寸如图1所示(节点编号为1～41)，长2m，矩形横截面尺寸0.03m×0.05m。其他材料参数包括：弹性模量E＝205GPa；密度ρ＝7800kg/m3。有限元建模采用欧拉-伯努利梁单元，将梁划分成40个单元(1～40)，从左至右顺序编号。为了验证该方法识别一处损伤和多处损伤的能力，设计如下两个损伤工况：(1)损伤工况一：模拟简支梁第8号单元的刚度减少30％；(2)损伤工况二：模拟简支梁第8、22、36号单元刚度分别减少20％，25％和15％。由于测量误差的客观存在，在数值算例的验证中加入了一定程度的白噪声干扰。在本发明数值模拟算例中，统一取噪声水平10％。通过移动单位竖向力在简支梁模型上加载确定影响线，并选择梁的1/4跨、1/2跨和3/4跨位置(对应于有限元模型的第11、21、31号节点)作为竖向位移响应的输出位置。照此可分别得到无损状态与损伤工况一状态下的挠度影响线DILu和DILd，进一步可得损伤前后挠度影响线变化量ΔZ。图2显示了1/4、1/2和3/4跨位置损伤前后的挠度影响线，从中可发现损伤前后的影响线区别并不明显。故仅从损伤前后的影响线，难以直接判断损伤和定位损伤位置。由公式(24)计算的影响线变化量，考虑了10％噪声水平的白噪声后，如图3所示，仍能通过曲线上峰值出现的位置，定出损伤的大致位置。1/4跨位置的影响线变化量峰值要大于1/2跨和3/4跨的结果，原因是损伤出现在8号单元位置，最靠近1/4跨位置，其次是1/2跨位置，离3/4跨位置最远。基于图3的结果可知，此时S和ΔZ都已确定。按照上节的理论对刚度矩阵分解组装，可构造得式(25)，然后采用有约束的最小二乘进行求解。图4展示了采用单个输出响应(1/2跨位置处的挠度影响线)进行损伤量化时的结果，此时仅仅能够得到一个可接受但不算准确的识别结果，此时，柔度系数矩阵的行数与一条影响线的离散点数量相同，但是略少于单元数。损伤位置虽然能够较好地识别出来，但损伤量化最大识别误差约达到了7％，其他非损伤位置也出现了些峰值。之所以出现这么大的误差，主要是由于以下两个原因：(1)柔度系数矩阵在这个情况下并非方阵，其行数小于列数，即未知量个数大于求解的等式个数，这会导致识别结果中出现较大误差；(2)噪声干扰不可忽略。除此之外，本实施例采用不同数量输出响应对损伤量化结果的影响。当采用三个输出响应共同进行损伤量化时，其识别结果见图5。不仅可准确地定位损伤位置，而且损伤量化的识别误差也非常小(<1％)，结果验证了这种基于挠度影响线损伤量化方法的有效性。为了验证此种方法是否适用于识别多处损伤。随后，模拟了简支梁上第8、22、36号单元刚度分别减少20％、25％和15％。此时，响应输出位置、噪声水平都与损伤工况一的相同。其输出位置的损伤前后挠度影响线及其变化绘于图6和7中，单单从挠度影响线或其变化这些结果，已经无法准确地进行损伤定位，只能粗略地判断有损伤存在。同时，考虑到在损伤工况一时，仅仅使用单一挠度影响线对简支梁的单点损伤进行损伤量化，其结果并非十分理想，所以针对于损伤工况二，这里选择3条挠度影响线共同进行损伤量化。采用上节所述理论，基本的识别框架与损伤工况一相同，其识别结果可见于图8，可以发现：(1)该方法可非常准确地定位出多处损伤位置，并未出现误判；(2)损伤量化结果非常接近于真实值，最大识别误差仅约为2.2％。这表明了此种基于DIL的损伤量化方法可用于多点损伤检测，并不依赖于一个“可视化”的影响线变化结果，即不依赖于由影响线变化的峰值来判断损伤位置。为了验证该方法是否适用于超静定结构，这里构造了一个两跨连续梁的数值模型。图9(节点编号为1～81，单元编号为1～80)展示了所应用的两跨连续梁数值模型，其截面尺寸与上节简支梁相同(0.03m×0.05m)，每跨长2m并划分40个单元。选择左跨1/4、左跨跨中和右跨跨中位置的竖向位移作为输出响应。将左跨的第8、22号单元和右跨的56号单元抗弯刚度分别减小30％，25％和15％。在此工况中，采用三个输出响应对损伤进行量化，识别结果见于图10中(识别误差为3.9％)。从图中可以推断，这种方法有希望应用于更复杂的结构。实施例2：实验室简支铝梁损伤量化简支铝梁采用箱型截面，长3.16m，高0.025m，宽0.15m，箱壁厚0.0015m。其有限元模型正视图和横截面如图11所示。模型更新后的杨氏模量为E＝6.9×1010Pa，采用2.47Kg的质量块按照特定间距(模型划分的单元间距)进行静载加载，以模拟移动竖向单位力。选择性地在梁的1/4跨、1/2跨、5/8跨和3/4跨位置布置位移计，采样频率为50Hz。除此之外，为了模拟损伤和定位损伤，整根梁被划分为32个区域，并从左至右进行编号，除了起始端的区域范围是8cm外其余都是10cm。这也是为了方便后续的模型参数更新。下面将对此实验所模拟的损伤工况进行描述：损伤工况一：在进行有损阶段实验时，在梁从左端算起2.205～2.255m位置(23号区域)处切割一个口以模拟第一处损伤，其惯性矩减少了55％(详细可见图12)。损伤工况二：在这之后，在梁1/4跨位置附近切割了第2个口，将其惯性矩减少30％，以模拟第二处损伤(见图12)。在图12中，节点编号为1～33，单元编号为1～32，箱形截面长3.16m，高0.025m，宽0.15m，箱壁厚0.0015m；标记D1：0.625m，D2：0.60m。此实验通过静载加载重物的方式施加荷载，输出上述4个位置的位移计响应数据，进而得到其对应的挠度影响线。除此之外，需要强调的是，本发明提出的损伤程度量化方法，需有无损状态下的整体刚度矩阵K和整体柔度矩阵F，进而构造柔度系数矩阵。即要求基于实测数据更新针对该铝梁建立的有限元模型，模型参数更新的准确性直接影响此种方法后续柔度矩阵构造和损伤参数的求解。因此，这里根据无损条件下的实测挠度影响线数据，对建立的有限元模型进行参数更新，更新后模型的输出位置响应与实测响应对比如图13所示，图中，exp1/4、exp1/2和exp3/4分别表示实验梁1/4跨、1/2跨和3/4跨位置的实测挠度影响线，FEM1/4、FEM1/2和FEM3/4则表示更新后的有限元模型相应位置的挠度影响线。由图可见，两者差距非常小，这验证了此时模型更新的准确性。损伤工况一下，安装了位移计位置的挠度影响线变化可见图14，从图中可见，虽然存在噪声干扰，试验的DIL变化仍旧可以较好地定位出损伤位置，并且距离损伤最近的3/4跨位置的挠度影响线变化最为显著，随后为5/8跨，1/2跨和1/4跨。同时，基于这些实验DIL变化数据和更新参数后的有限元模型，采用上述所提方法构造柔度系数矩阵以识别损伤位置及损伤程度，结果可见图15。即使仅仅使用单条DIL，损伤位置——单元23仍旧可以较好地被定位出来，而损伤程度的识别效果随着位移计距离损伤位置的远近有所差异，距离越近，其效果越好。由于距离损伤位置较远，1/4跨位置的位移计信息相对于其他的传感器信息，其信噪比较低，所以利用其识别的损伤程度误差最大，达到了12％。类似地，这里也输出了多传感器信息共同识别的结果(见图16)，当使用多个传感器时，非损伤位置都未出现大的峰值最大误差仅约为2％。上述结果表明：(1)距离损伤位置越近的输出响应，其损伤量化误差越小；(2)随着使用输出响应的增加，损伤识别效果越佳。同时，这些结果也证明了基于DIL进行损伤量化的实际可行性。图17是应用上述方法识别多处损伤的结果。由图可见，当仅仅使用1个传感器信息时，在区域1处出现了5％的识别误差。当同时利用3个传感器的信息时，区域1的识别误差得到了很大程度的降低，并且损伤位置——区域10和23，都被准确地被识别了出来。实验结果基本符合数值模拟的结论，即这种基于DIL的损伤识别方法不仅可以准确地实现损伤定位，同时拥有良好的损伤量化效果。本发明基于桥梁挠度影响线，除了可实现对桥梁局部损伤定位，更能准确量化损伤的程度。基于影响线的损伤指标对桥梁局部损伤更敏感，而对环境因素变化不敏感，较适用在运营环境下检测桥梁的局部损伤。相比传统基于灵敏度矩阵的损伤定位方法，类似灵敏度矩阵的构造更加简单方便，求解过程可不迭代，避免了数值求解的迭代不收敛问题，并且提高了求解速度。当前第1页1 2 3