基于单层感知机的欠定盲源分离源信号恢复方法与流程

本发明属于通信技术领域，更进一步涉及信号处理技术领域中的一种基于单层感知机的欠定盲源分离源信号恢复方法。本发明可以对军事通信信号，图像信号，生物医学信号进行处理，实现在混合矩阵已经估计完成的情况下欠定盲源分离源信号的恢复。

背景技术：

欠定盲源分离是在对传输信道参数未知且观测信号的数目小于源信号数目的情况下，仅仅利用观测信号将源信号估计出来。欠定盲源分离技术只需少量传感器来接收混合信号，不仅满足特定场合，还能节约成本。

现有的欠定盲源分离通常采用两阶段法，即先利用观测信号估计混合矩阵，再利用估计出的混合矩阵和观测信号恢复出源信号。在实际应用中，往往需要以较高的精度恢复源信号，但源信号恢复的时间复杂度也会相应的提高，因此，研究兼顾源信号恢复的时间复杂度和源信号恢复精度的方法成为欠定盲源分离中亟待解决的问题。

西安电子科技大学所拥有的专利技术“基于密度的欠定盲源分离方法”(申请号201310116467.8，申请日2013.04.03，授权号CN103218524B，授权日2016.01.20)中提出了一种基于密度的欠定盲源分离方法。该方法将观测信号去掉低能量采样数据后投影到右半超球面上，然后计算投影点的密度，删除密度较小的投影点，从而能够减少初始值对估计性能的影响，降低了计算复杂度。但是，该专利技术仍然存在的不足之处是，根据观测信号矩阵和估计完成的混合矩阵，采用线性规划法来恢复源信号，源信号的恢复精度易受误差的影响，在实际应用中很难保证以较高的精度实现源信号的恢复。

Vivekanand V等人在其发表的论文“RBF-network based sparse signal recovery algorithm for compressed sensing reconstruction”(Neural Networks，2015)中提出了一种基于径向基函数网络源信号恢复方法(RASR)。该方法先利用梯度下降法计算基于近似L0范数的近似最优值，然后利用梯度下降法对近似最优值进行修正使其满足欠定方程，提高了源信号恢复的精度。但是，该方法仍然存在的不足之处是，使用固定的迭代步长，源信号恢复精度和时间复杂度很难兼顾，在实际应用中很难保证以较快的速率实现源信号的恢复。

技术实现要素：

本发明的目的在于针对上述现有技术存在的不足，提出一种基于单层感知机的欠定盲源分离源信号恢复方法。本发明可以降低源信号恢复的复杂度，同时提高源信号恢复的精确度，兼顾源信号恢复的时间复杂度与精确度。

实现本发明目的的具体思路是：在压缩感知重构模型的基础上，引入单层感知机，寻找最优学习因子，在保持较高的源信号恢复精度的同时，降低计算的复杂度。

实现本发明目的的具体步骤如下：

(1)将采集到的通信信号存入观测信号矩阵；

(2)对观测信号矩阵进行聚类，得到混合矩阵；

(3)将欠定盲源分离的迭代次数初始化为1；

(4)按照下式，计算待恢复源信号列向量：

其中，表示待恢复源信号列向量，A表示混合矩阵，表示求伪逆操作，x(l)表示观测信号矩阵中的第l个列向量，l表示欠定盲源分离的迭代次数；

(5)赋值高斯参数：

(5a)搜索待恢复源信号列向量中的最大分量；

(5b)将搜索到的最大分量的值赋给高斯参数；

(6)更新待恢复源信号列向量：

(6a)将单层感知机法的迭代次数初始化为1；

(6b)利用最速下降法，计算单层感知机的增量；

(6c)将待恢复源信号列向量加上单层感知机的增量，得到更新后的待恢复源信号列向量；

(6d)将单层感知机法的迭代次数加1，得到单层感知机法的当前迭代次数；

(6e)判断单层感知机法的当前迭代次数是否小于等于M，若是，则执行步骤(6b)，否则，执行步骤(7)，其中，M表示待恢复源信号列向量的个数；

(7)将高斯参数乘以0.6，得到更新后的高斯参数；

(8)判断更新后的高斯参数是否大于10^-5，若是，则执行步骤(6)，否则，执行步骤(9)；

(9)存储利用单层感知机法更新后的待恢复源信号列向量；

(10)将欠定盲源分离的迭代次数加1，得到欠定盲源分离的当前迭代次数；

(11)判断欠定盲源分离的当前迭代次数是否小于等于观测信号矩阵的列数，若是，执行步骤(4)，否则，执行步骤(12)；

(12)获得恢复源信号矩阵：

将欠定盲源分离迭代得到的所有待恢复源信号列向量组成恢复源信号矩阵。

本发明与现有技术相比具有以下优点：

第一，由于本发明采用了单层感知机法更新待恢复的源信号列向量，克服了现有技术中欠定盲源分离源信号恢复精度易受噪声和误差影响的缺点，使得本发明能显著提高源信号恢复的精度。

第二，由于本发明采用最速下降法计算最优学习因子，克服了现有技术中欠定盲源分离源信号恢复过程中时间复杂度偏高的问题，使得本发明能保持较高恢复精度的同时快速的恢复源信号。

附图说明

图1是本发明的流程图；

图2是本发明的仿真图。

具体实施方式

下面结合附图对本发明做进一步的描述。

参照附图1，本发明的具体步骤如下。

步骤1，将采集到的通信信号存入观测信号矩阵。

步骤2，对观测信号矩阵进行聚类，得到混合矩阵。

对观测信号矩阵进行聚类的具体实施步骤如下：

剔除观测信号矩阵中全为0值的列，将剩余的列组成待恢复信号矩阵；选取待恢复信号矩阵中第一个分量为负数的列向量，对该列向量的所有元素乘以-1得到翻转列向量；将翻转列向量和未被选取的列向量组成翻转矩阵；对翻转矩阵进行归一化处理得到归一化信号矩阵；利用K-均值聚类方法，对归一化信号矩阵中的所有列向量进行聚类，得到所有的聚类中心；将所有的聚类中心组成混合矩阵。

步骤3，将欠定盲源分离的迭代次数初始化为1。

步骤4，计算待恢复源信号列向量。

按照下式，计算待恢复源信号列向量：

其中，表示待恢复源信号列向量，A表示混合矩阵，表示求伪逆操作，x(l)表示观测信号矩阵中的第l个列向量，l表示欠定盲源分离的迭代次数。

步骤5，赋值高斯参数。

搜索待恢复源信号列向量中的最大分量，将搜索到的最大分量的值赋给目标参数。

步骤6，更新待恢复源信号列向量。

第1步，将单层感知机法的迭代次数初始化为1。

第2步，按照下式，计算高斯对角矩阵：

$D=diag\[e^{-\frac{{\hat{s}}_1}{2{\mathrm{\σ}}^2}},e^{-\frac{{\hat{s}}_2}{2{\mathrm{\σ}}^2}},...,e^{-\frac{{\hat{s}}_N}{2{\mathrm{\σ}}^2}}\]$

其中，D表示高斯对角矩阵，diag[·]表示设定对角元操作，e^(·)表示以自然数为底数的求幂操作，σ表示高斯参数，N表示传感器的总数，表示待恢复源信号列向量的第一个分量，表示待恢复源信号列向量的第二个分量，表示待恢复源信号列向量的第N个分量。

第3步，按照下式，计算最优学习因子：

$\mathrm{\μ}=\frac{\left|\right|A_j^T(x_j-A_j\hat{s})-D\hat{s}\left|\right|}{\left|\right|(A_j^T{A}_j+D)\left(A_j^T\right(x_j-A_j\hat{s})-D\hat{s}\left)\right||}$

其中，μ表示最优学习因子，A_j表示混合矩阵的第j个行向量，(·)^T表示转置操作，x_j表示观测信号向量的第j个元素，表示待恢复源信号列向量，D表示高斯对角矩阵；||·||表示求模操作。

第4步，按照下式，计算单层感知机的增量：

$\mathrm{\Δ}=\mathrm{\μ}\left(A_j^T\right(x_j-A_j\hat{s})-D\hat{s})$

其中，Δ表示单层感知机的增量，μ表示最优学习因子，A_j表示混合矩阵的第j个行向量，(·)^T表示转置操作，x_j表示观测信号向量的第j个元素，表示待恢复源信号列向量，D表示高斯对角矩阵。

第5步，将待恢复源信号列向量加上单层感知机的增量，得到更新后的待恢复源信号列向量。

第6步，将单层感知机法的迭代次数加1，得到单层感知机法的当前迭代次数。

第7步，判断单层感知机法的当前迭代次数是否小于等于M，若是，则执行步骤6中的第2步，否则，执行步骤7，其中，M表示待恢复源信号列向量的个数。

步骤7，将高斯参数乘以0.6，得到更新后的高斯参数。

步骤8，判断更新后的高斯参数是否大于10^-5，若是，则执行步骤6，否则，执行步骤9。

步骤9，存储利用单层感知机法更新后的待恢复源信号列向量。

步骤10，将欠定盲源分离的迭代次数加1，得到欠定盲源分离的当前迭代次数。

步骤11，判断欠定盲源分离的当前迭代次数是否小于等于观测信号矩阵的列数，若是，执行步骤4，否则，执行步骤12。

步骤12，获得恢复源信号矩阵。

将欠定盲源分离迭代得到的所有待恢复源信号列向量组成恢复源信号矩阵。

下面结合仿真图对本发明做进一步的描述。

1.仿真条件：

本发明的仿真实验是在硬件环境为Pentium(R)Dual-Core CPU E5300@2.60GHz，软件环境为32位Windows操作系统的条件下进行的。

仿真参数设置为，使用matlab软件产生随机稀疏信号，源信号数目为5，采集次数为1000。分别对基于密度的欠定盲源分离方法、基于径向基函数网络的源信号恢复方法(RARS)和本发明的提出方法进行仿真。

2.仿真内容与结果分析：

本发明的仿真实验是使用本发明、基于密度的欠定盲源分离方法和RASR方法对稀疏信号进行恢复，得到恢复的源信号。

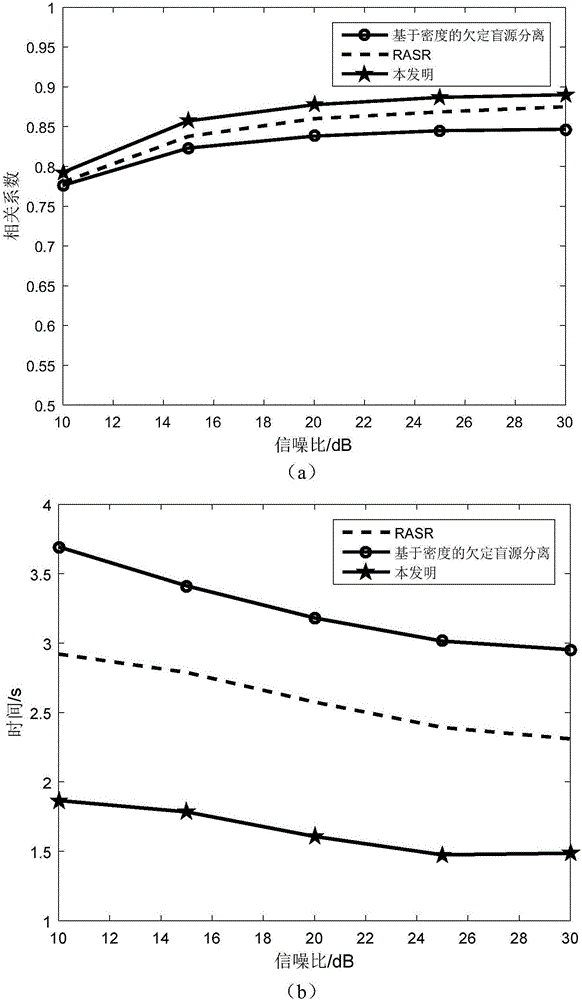
图2(a)是采用本发明和现有技术的两个方法(基于密度的欠定盲源分离方法和RASR方法)在稀疏度为0.8的情况下，分别对稀疏信号进行恢复得到的源信号的恢复精度的比较图。图2(a)中的横坐标表示信噪比，纵坐标表示相关系数。图2(a)中以五角星标示的曲线表示本发明所得到的相关系数随信噪比变化的曲线，以圆形标示的曲线表示基于密度的欠定盲源分离方法所得到的相关系数随信噪比变化的曲线，以点划线标示的曲线表示基于径向基函数网络的源信号恢复方法(RASR)所得到的相关系数随信噪比变化的曲线。

图2(b)是采用本发明和现有技术的两个方法(基于密度的欠定盲源分离方法和RASR方法)在稀疏度为0.8的情况下，分别对稀疏信号进行恢复得到的源信号的时间复杂度的比较图。图2(b)中的横坐标表示信噪比，纵坐标表示时间，运算时间越多表示源信号的时间复杂度越高。图2(b)中以五角星标示的曲线表示本发明所得到的运算时间随信噪比变化的曲线，以圆型标示的曲线表示基于密度的欠定盲源分离方法所得到的运算时间随信噪比变化的曲线，以点划线标示的曲线表示基于径向基函数网络的源信号恢复方法(RASR)所得到的运算时间随信噪比变化的曲线。

由图2(a)可见，在信噪比为10dB与30dB范围内，本发明所恢复的源信号的相关系数均大于基于密度的欠定盲源分离方法和RASR方法所恢复的源信号的相关系数。

由图2(b)可见，在信噪比为10dB到30dB范围内，本发明的时间复杂度均小于基于密度的欠定盲源分离方法和RASR方法的时间复杂度。

综上所述，在低信噪比和高信噪比情况下，本发明在时间复杂度和精确度方面均优于现有技术；在稀疏度较小的情况下，本发明能够在保持较高恢复精度的同时，显著降低了时间复杂度；在稀疏度较高的情况下，本发明获得很高的恢复精度。因此，本发明在保证源信号恢复精度的情况下，显著降低了恢复源信号的时间复杂度。