双线盾构隧道施工对地下管线安全造成影响的评估方法与流程

本发明涉及双线盾构垂直穿越地下管线的安全监管技术，具体涉及一种双线盾构隧道施工对地下管线安全造成影响的评估方法。
背景技术：
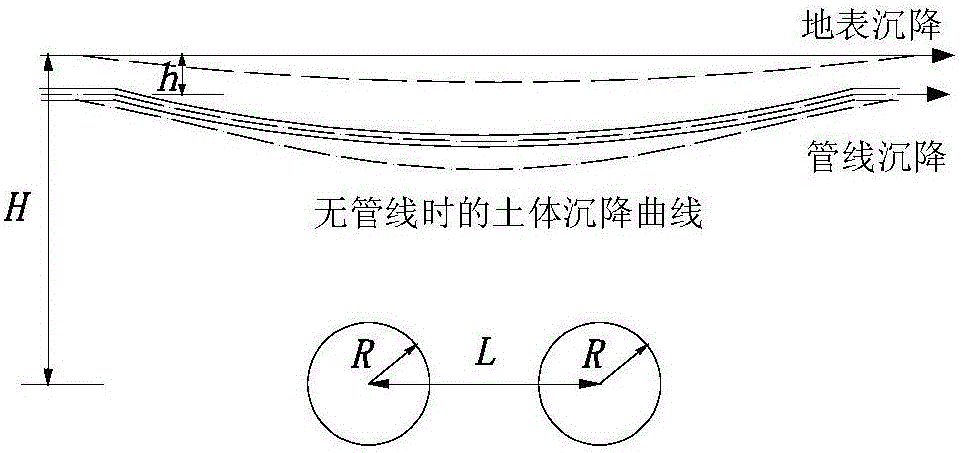
：地下管线是维系城市地上地下空间、保证城市整体运行的基础设施。由于地铁属于浅埋隧道，其施工扰动会对管线安全构成威胁，随着越来越多的城市开始大规模建设地铁工程，地铁施工引发管线损坏的事故也屡屡发生。这些事故给社会生产、生活带来巨大损失，因此亟需建立一套管线安全判别体系，预防事故的发生。目前关于管线安全性判别的研究方法可分为两类。第一类方法[1-2]是将隧道施工引起的管线受力变形的计算值，与规范中的安全允许值比较，以此判断管线是否安全。而实际工程中：一方面，管线埋置于地下且受力状态一直在改变，不容易及时测量其受力变形；另一方面，当通过计算发现管线存在危险时，管线可能已经破坏，因此实用性较低。第二类方法[3-4]是通过地表沉降这一指标反映管线状态，实用性较强，因为地铁施工时必须对地表沉降进行监测。但研究成果还不成熟，不足之处主要体现在未对管线受力变形的计算公式、管线处土体沉降与地表沉降的联系公式进行更新(应采用最新研究成果)，且未明确提出地表沉降与管线受力变形的计算关系式。两类方法的研究均未考虑管线的老化。且现有研究局限于单线盾构隧道施工，但实际工程往往采用双线平行盾构隧道进行施工。技术实现要素：本发明的目的是克服现有技术中不足，提供一种双线盾构隧道施工对地下管线安全造成影响的评估方法。本专利将管线受力变形与地表沉降联系起来，分别提出双线盾构施工情况下，邻近连续管线应变与地表沉降关系式和非连续管线接头转角与地表沉降关系式；并考虑管线老化，建立了一种双线盾构隧道施工对地下管线安全造成影响的评估方法。为了达到上述目的，小发明是通过以下技术方案实现的：本发明提出一种双线盾构隧道施工对地下管线安全造成影响的评估方法，主要分为以下4个步骤：一、通过修正PECK公式，建立地表沉降与土体损失关系。以右侧隧道先开挖为例，土体中任意一点(x，z)的沉降公式为：Sz(x)=Smax,f(1-z/H)nexp[-(x-0.5L)22if2(1-z/H)2n]+Smax,l(1-z/H)nexp[-(x+0.5L)22il2(1-z/H)2n]]]>式中：H为盾构轴线埋深，单位符号为mm；Sz(x)为双线盾构隧道施工引起的总的土体沉降，单位符号为mm；x为距双线盾构隧道中轴线的横向水平距离，单位符号为mm；z为距地表的距离，单位符号为mm；Smax，f、Smax，l分别表示先行隧道和后行隧道轴线正上方地表沉降值，单位符号为mm，π为圆周率，一般取3.14；ηf、ηl分别为先行和后行隧道产生的土体损失率；if、il分别为先行和后行隧道的地表沉降槽宽度系数，单位符号为mm；n为与隧道半径和土质条件有关的影响系数，对于黏性土，n的取值范围在[0.35～0.85]之间；对于砂土，n的取值范围在[0.85～1.0]之间；R为盾构半径，单位符号为mm；L为两条隧道轴线水平间距，单位符号为mm。二、管线受力变形与土体损失的关系式。(1)对于非连续管线，根据弹性地基梁理论，可以得到管线受隧道开挖影响的变形微分方程为：EI∂4w∂x4+kdw=kSz(x)d]]>式中：EI为管线抗弯刚度，单位符号为Pa；k为管线平面处的地基反力系数，单位符号为Pa；d为管线外径，单位符号为mm；w为管线的竖向挠度，单位符号为mm。解微分方程，可得管线纵向中心点处受到的最大弯矩Mmax为：Mmax=∫-∞∞dM(x)=∫-∞∞kSz(x)d4βexp(-βx)(cosβx-sinβx)dx.]]>式中：由此笔者提出管线在隧道开挖影响范围内任意一点(x0，h)的弯矩M(x)计算公式为：M(x)=EIβ3πR2ηfif2π(1-hH)-n·∫-∞+∞(cos(β|x-0.5L-x0|)-sin(β|x-0.5-L-x0|))·exp[-(x-0.5L)22if2(1-h/H)2n-β|x-0.5L-x0|]dx+EIβ3πR2ηlil2π(1-hH)-n·∫-∞+∞(cos(β|x+0.5L-x0|)-sin(β|x+0.5-L-x0|))·exp[-(x+0.5L)22il2(1-h/H)2n-β|x+0.5L-x0|]dx]]>式中：x0为坐标系上的任意一点坐标，单位符号为mm；h为管线轴线埋深，单位符号为mm。(2)对于连续管线，考虑管土效应，则管线的真实沉降一般会小于无管线存在时的土体沉降。理论上需要求出管线的真实沉降，来计算其真实接头转角。但由于弹性地基梁法求解管线位移比较困难，为简便计算，本文假定非连续管线沉降与无管线存在时的土体沉降一致。这种处理方法会比实际情况保守，不影响安全性判断。由于双线隧道水平间距L的不同，双线盾构施工引起的土体沉降曲线可能出现V型或W型。若施工时土体沉降曲线呈W型，其引起管线接头转角最大值分别出现在两条隧道轴线的下上方，则计算先行、后行盾构隧道轴线上方土体沉降时，可以以单线盾构隧道为计算模型。可设ηf＝ηl，则管线接头转角公式：θ=2tan-1{Sz(0)i(s)2π}]]>即式中：θ为管线和隧道垂直时产生的接头转角，单位符号为°；i(s)为地表沉降槽宽度系数，单位符号为mm。变换化简，可得土体损失率与管线接头转角θ的关系式：ηf=2[i(s)]2tan(θ/2)R2(1-h/H)2n]]>若施工中土体沉降曲线呈V型，其引起管线接头转角最大值出现在双线隧道正中间，可设ηf＝ηl、if＝il。以ηf为标准，则可得到土体损失率与管线接头转角θ的关系式：ηf=[i(s)]2tan(θ/2)R2exp{-0.25L22[i(s)]2(1-h/H)2n}]]>三、建立地表沉降与管线受力变形的关系式。将M(x)或θ用规范中的管线应变或转角安全允许值带入，求出管线安全前提下对应的土体损失率安全允许值[ηf]。最后，通过修正的二维Peck公式建立土体损失率与地表沉降的关系：[S′max(x)]=πR2[ηf]if2πexp[-(x-0.5L)22if2]+πR2[ηl]il2πexp[-(x+0.5L)22il2]]]>式中：[S′max(x)]为地表沉降安全允许曲线，单位符号位mm。四、考虑与时间相关的折减系数。根据城市给水排水技术规范，地下管道结构的设计使用年限不低于50年，安全等级不小于二级。假设管线设计使用年限为50年，根据工程结构可靠性设计统一标准，并结合结构可靠指标，规定50年后可靠指标不小于0.5，即α仍有0.5的富余，则：α＝1-t/100，式中t为管线年龄(年)。考虑管线老化，则地表沉降安全允许曲线的修正计算公式为：[Smax(x)]=απR2[ηf]if2πexp[-(x-0.5L)22if2]+απR2[ηl]il2πexp[-(x+0.5L)22il2]]]>式中：[Smax(x)]为考虑管线老化后修正的地表沉降安全允许曲线，单位符号位mm。根据上式，若实际监测的地表沉降曲线大于求得的地表沉降安全允许曲线，则表明管线存在危险，需要对施工条件进行改进，将地表沉降控制在允许范围内；若实际监测的地表沉降曲线小于求得的地表沉降安全允许曲线，则表明管线状态良好，可按目前的施工条件继续施工。本发明的有益效果如下：本专利考虑了实际情况中管线的老化问题，结合相关规范，成果以地表沉降为指标来监测地下管线安全状态，将难以测量观察的管线状态转化为直观可见的地表沉降，简化了监测方法。施工过程中，场地人员只需对地表沉降进行监测，即可同时对管线的安全状态进行评估。实际工程中，盾构半径R、盾构埋深H、管线埋深h、双线盾构间距L、地表沉降槽宽度系数i(s)、与隧道半径和土质条件有关的影响系数n、管线抗弯刚度EI、管线平面处的地基反力系数k、管线外径d、管线应变或转角安全允许值M(x)或θ均为已知条件，带入地表沉降安全允许曲线公式即可得到地表沉降安全允许曲线。若实际监测的地表沉降曲线大于求得的地表沉降安全允许曲线，则表明管线存在危险，需要对施工条件进行改进，将地表沉降控制在允许范围内；若实际监测的地表沉降曲线小于求得的地表沉降安全允许曲线，则表明管线状态良好，可按目前的施丁条件继续施工。附图说明图1为本发明中涉及到的非连续管线W型计算模型示意图；图2为本发明中涉及到的非连续管线V型计算模型示意图；图3本发明的基本流程图。图4本发明中所述的评估方法(即图4中简称为本文方法)与实测数据的比较示意图。具体实施方式下面结合说明书附图对本发明的技术方案作进一步说明：如图1～4所示，本发明提出一种双线盾构隧道施工对地下管线安全造成影响的评估方法的具体实施例，主要分为以下4个步骤：三、通过修正PECK公式，建立地表沉降与土体损失关系。以右侧隧道先开挖为例，土体中任意一点(x，z)的沉降公式为：Sz(x)=Smax,f(1-z/H)nexp[-(x-0.5L)22if2(1-z/H)2n]+Smax,l(1-z/H)nexp[-(x+0.5L)22il2(1-z/H)2n]]]>式中：H为盾构轴线埋深，单位符号为mm；Sz(x)为双线盾构隧道施工引起的总的土体沉降，单位符号为mm；x为距双线盾构隧道中轴线的横向水平距离，单位符号为mm；z为距地表的距离，单位符号为mm；Smax，f、Smax，l分别表示先行隧道和后行隧道轴线正上方地表沉降值，单位符号为mm，π为圆周率，一般取3.14；ηf、ηl分别为先行和后行隧道产生的土体损失率；if、il分别为先行和后行隧道的地表沉降槽宽度系数，单位符号为mm；n为与隧道半径和土质条件有关的影响系数，对于黏性土，n的取值范围在[0.35～0.85]之间；对于砂土，n的取值范围在[0.85～1.0]之间；R为盾构半径，单位符号为mm；L为两条隧道轴线水平间距，单位符号为mm。四、管线受力变形与土体损失的关系式。(1)对于非连续管线，根据弹性地基梁理论，可以得到管线受隧道开挖影响的变形微分方程为：EI∂4w∂x4+kdw=kSz(x)d]]>式中：EI为管线抗弯刚度，单位符号为Pa；k为管线平面处的地基反力系数，单位符号为Pa；d为管线外径，单位符号为mm；w为管线的竖向挠度，单位符号为mm。解微分方程，可得管线纵向中心点处受到的最火弯矩Mmax为：Mmax=∫-∞∞dM(x)=∫-∞∞kSz(x)d4βexp(-βx)(cosβx-sinβx)dx.]]>式中：由此笔者提出管线在隧道开挖影响范围内任意一点(x0，h)的弯矩M(x)计算公式为：M(x)=EIβ3πR2ηfif2π(1-hH)-n·∫-∞+∞(cos(β|x-0.5L-x0|)-sin(β|x-0.5-L-x0|))·exp[-(x-0.5L)22if2(1-h/H)2n-β|x-0.5L-x0|]dx+EIβ3πR2ηlil2π(1-hH)-n·∫-∞+∞(cos(β|x+0.5L-x0|)-sin(β|x+0.5-L-x0|))·exp[-(x+0.5L)22il2(1-h/H)2n-β|x+0.5L-x0|]dx]]>式中：x0为坐标系上的任意一点坐标，单位符号为mm；h为管线轴线埋深，单位符号为mm。(3)对于连续管线，考虑管土效应，则管线的真实沉降一般会小于无管线存在时的土体沉降。理论上需要求出管线的真实沉降，来计算其真实接头转角。但由于弹性地基梁法求解管线位移比较困难，为简便计算，本文假定非连续管线沉降与无管线存在时的土体沉降一致。这种处理方法会比实际情况保守，不影响安全性判断。由于双线隧道水平间距L的不同，双线盾构施工引起的土体沉降曲线可能出现V型或W型。若施工时土体沉降曲线呈W型，其引起管线接头转角最大值分别出现在两条隧道轴线的正上方，如图1。则计算先行、后行盾构隧道轴线上方土体沉降时，可以以单线盾构隧道为计算模型。可设ηf＝ηl，则管线接头转角公式：θ=2tan-1{Sz(0)i(s)2π}]]>即式中：θ为管线和隧道垂直时产生的接头转角，单位符号为°；i(s)为地表沉降槽宽度系数，单位符号为mm。变换化简，可得土体损失率与管线接头转角θ的关系式：ηf=2[i(s)]2tan(θ/2)R2(1-h/H)2n]]>若施工中土体沉降曲线呈V型，其引起管线接头转角最大值出现在双线隧道正中间，如图2。可设ηf＝ηl、if＝il。以ηf为标准，则可得到土体损失率与管线接头转角θ的关系式：ηf=[i(s)]2tan(θ/2)R2exp{-0.25L22[i(s)]2(1-h/H)2n}]]>三、建立地表沉降与管线受力变形的关系式。将M(x)或θ用规范中的管线应变或转角安全允许值带入，求出管线安全前提下对应的土体损失率安全允许值[ηf]。最后，通过修正的二维Peck公式建立土体损失率与地表沉降的关系：[S′max(x)]=πR2[ηf]if2πexp[-(x-0.5L)22if2]+πR2[ηl]il2πexp[-(x+0.5L)22il2]]]>式中：[S′max(x)]为地表沉降安全允许曲线，单位符号位mm。五、考虑与时间相关的折减系数。根据城市给水排水技术规范，地下管道结构的设计使用年限不低于50年，安全等级不小于二级。假设管线设计使用年限为50年，根据工程结构可靠性设计统一标准，并结合结构可靠指标，规定50年后可靠指标不小于0.5，即α仍有0.5的富余，则：a＝1-t/100，式中t为管线年龄(年)。考虑管线老化，则地表沉降安全允许曲线的修正计算公式为：[Smax(x)]=απR2[ηf]if2πexp[-(x-0.5L)22if2]+απR2[ηl]il2πexp[-(x+0.5L)22il2]]]>式中：[Smax(x)]为考虑管线老化后修正的地表沉降安全允许曲线，单位符号位mm。根据上式，若实际监测的地表沉降曲线大于求得的地表沉降安全允许曲线，则表明管线存在危险，需要对施工条件进行改进，将地表沉降控制在允许范围内；若实际监测的地表沉降曲线小于求得的地表沉降安全允许曲线，则表明管线状态良好，可按目前的施工条件继续施工。本专利考虑了实际情况中管线的老化问题，结合相关规范，成果以地表沉降为指标来监测地下管线安全状态，将难以测量观察的管线状态转化为直观可见的地表沉降，简化了监测方法。施工过程中，场地人员只需对地表沉降进行监测，即可同时对管线的安全状态进行评估。实际工程中，盾构半径R、盾构埋深H、管线埋深h、双线盾构间距L、地表沉降槽宽度系数i(s)、与隧道半径和土质条件有关的影响系数n、管线抗弯刚度EI、管线平面处的地基反力系数k、管线外径d、管线应变或转角安全允许值M(x)或θ均为已知条件，带入地表沉降安全允许曲线公式即可得到地表沉降安全允许曲线。若实际监测的地表沉降曲线大于求得的地表沉降安全允许曲线，则表明管线存在危险，需要对施工条件进行改进，将地表沉降控制在允许范围内；若实际监测的地表沉降曲线小于求得的地表沉降安全允许曲线，则表明管线状态良好，可按目前的施工条件继续施工。本发明专利中的基本流程示意图见图3。另外本发明还参考了孙宇坤[5]一文中的实测数据，对本专利方法进行验证。文献中未提到管线使用年限，因此不考虑管线老化。计算得到管线平面处土体沉降曲线呈V型，先行隧道的[ηf]＝0.817％，[Smax(x)]＝18.3mm，即两条隧道中轴线的地表沉降超过18.3mm后管线有破坏的危险。图4为实测数据和本文方法计算值的比较。如图所示，实测地表沉降曲线在本文方法计算曲线范围内，实测最大地表沉降值14.12mm也小于本文方法计算得到的[Smax(x)]值，判断管线安全。实际工程中管线未破坏，证明了本文方法的可靠性。上述实施例是对本发明的说明，不是对本发明的限定，任何对本发明简单变换后的方案均属于本发明的保护范围。其中：对木发明中所涉及的一些引用文献做如下简单说明：[1]向卫国.隧道开挖引起地下管线变形和安全性状的研究[D].北京：中国铁道科学研究院，2011.XIANGWei-guo.Studyontheeffectsandsafetyofexistingpipelineinducedbythetunneling[D].Beijing：ChinaAcademyofRailwaySciences，2011.[2]裴超.隧道施工对邻近地下管线的影响研究[J].山西建筑，2008，34(12)：325-327.PEIChao.Studytheinfluenceoftunnelconstructionontheneighboringundergroundpipeline[J].ShanxiArchitecture，2008，34(12)：325-327.[3]周成君.地铁盾构隧道施工对城市地下管线的影响研究[D].南京：南京林业大学，2010.ZHOUCheng-jun.Studyoneffectofsubwayshieldtunnelconstructiononadjacentburiedpipelines[D].Nanjing：NanjingForestryUniversity，2010.[4]李林.超大直径盾构穿越高危管线安全度判定方法及实测研究[J].现代隧道技术，2014，51(5)：134-138.LILin.Thejudgmentmethodandfieldresearchregardingsafetyforanextra-largediametershieldpassingunderhigh-riskpipelines[J].ModernTunnellingTechnology，2014，51(5)：134-138.[5]孙宇坤，吴为义，张土乔.软土地区盾构隧道穿越地下管线引起的管线沉降分析[J].中国铁道科学，2009，30(1)：80-85.SUNYu-kun，WUWei-yi，ZHANGTu-qiao.Analysisonthepipelinesettlementinsoftgroundinducedbyshieldtunnelingacrossburiedpipeline[J].ChinaRailwayScience，2009，30(1)：80-85.当前第1页1 2 3