一种桥梁挠度温度效应和长期挠度的分离方法与流程

本发明涉及桥梁监控研究领域，特别涉及一种桥梁挠度温度效应和长期挠度的分离方法。
背景技术：
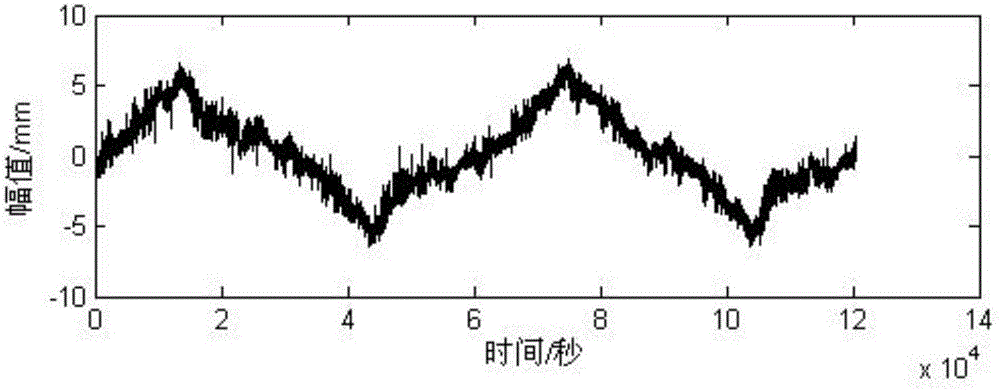
：挠度是桥梁安全评价中至关重要的参数，荷载与环境的作用、结构材料的变异都可以通过挠度的变化表现出来。精确获取挠度监测信号各响应分量，是正确诊断桥梁结构病害、准确评估其工作状态，以及分析病害发生机理的前提和基础。在桥梁挠度的实际监测数据中，其所含有的季节特征、趋势特征以及不规则变化是无法直接观察到的，也就不能直接从中研究温度场对挠度的影响，只能通过人为的方法去分解出来挠度的温度效应。这种方法对人的经验有很大的依赖，造成数据的不准确。为此，寻求一种能够准确分离桥梁挠度温度效应和长期挠度的方法，具有重要意义。技术实现要素：本发明的目的在于克服现有技术的缺点与不足，提供一种桥梁挠度温度效应和长期挠度的分离方法，该方法能够解决桥梁健康监控系统中挠度测量各组成成分的分离问题，精确获取挠度监测信号各响应分量，为正确诊断桥梁结构病害、准确评估其工作状态，以及分析病害发生机理提供基础。为解决上述技术问题，本发明采用如下技术方法予以实现：一种桥梁挠度温度效应和长期挠度的分离方法，包括步骤：(1)采集挠度数据，应用局部切空间排列方法(LocalTangentSpaceAlignment，LTSA)对N小时内时间序列的确定性成分与随机干扰成分进行分离，去掉随机干扰数据；(2)按照挠度数据的时间特征，对区段内确定性成分数据以小时为单位进行多尺度数据融合处理，得到第一融合数据的时间序列；(3)构建IHSSM模型(ImprovedHarrisonandStevensSeasonalModel,结构时间序列模型)，应用IHSSM模型对第一融合数据的时间序列进行分离，分离出第一季节项和第一趋势项，第一季节项即是日温度效应；(4)将分离出的第一趋势项以天(24小时)为单位进行多尺度数据融合处理，得到第二融合数据；(5)将第二融合数据分成若干片段，将片段中相同位置的数据组成若干数据组，对每组数据建立IHSSM模型分离第二季节项和第二趋势项，然后再将所有组的第二季节项和第二趋势项分别组合起来，形成第三季节项和第三趋势项，第三季节项为年温度效应，第三趋势项为长期挠度。优选的，步骤(1)中，采集挠度数据的步骤是：安装在桥梁上的各个传感器采集得到挠度信号，然后经低通滤波处理后得到挠度数据；每个传感器得到的挠度数据S(k)为：S(k)＝S1(k)+S2(k)+S3(k)+ε(k)(1)式中，S1(k)为日温度挠度信号、S2(k)为年温度挠度信号、S3(k)长期挠度信号(包括混凝土收缩徐变挠度、预应力损失及结构损伤等的挠度效应),ε(k)为随机时间序列。采用低通滤波预先处理用于剔除活荷载效应影响。优选的，步骤(1)中，应用局部切空间排列方法分离确定性成分和随机干扰成分的步骤是：(1-1)设挠度数据总长度为Lsecond，单位为秒，首先把序列S(k)在高维空间重构，当相空间嵌入维数为m时S(k)＝f(S(k-m),S(k-m+1),…,S(k-1))(2)对时间序列相空间重构得：p(j,k)＝S(k+(j-1)τ)(3)τ为时间延迟；(1-2)局部邻域构造：取式(3)组成的时间序列相空间样本点，记为xi，求样本点的邻域Xi＝[xi1,xi2,…,xik]，Xi为xi包括自身在内的k个临近点构成的集合；(1-3)局部坐标线性拟合：对Xi中心化，得为邻域数据均值，其中ek为k维单位向量；对进行SVD分解，记其中Λi为奇异值按降序排列的对角阵；(1-4)局部坐标系统的排列：构造其中Si是满足[x1,x2,…,xL]Si＝[xi1,xi2,…,xik]的选择矩阵，L为样本点数目，计算B对应的最小d+1个特征值对应的特征向量t1,t2,…,td+1，则T＝[t2,t3,…,td+1]即为整个样本的低维空间流形坐标；(1-5)通过式(4)把得出的低维空间流形坐标映射回原时间序列相空间：yi=x‾i+QiLi(ti-ti‾)---(4)]]>其中：Li为Xi到T的转化矩阵，随机成分为：σi＝xi-yi(5)然后通过下式分别把yi、σi映射到一维时间序列：S^(k)=Σt∈{Ii(j,k)}ytCk---(6)]]>σ^(k)=Σt∈{Ii(j,k)}σtCk---(7)]]>其中Ii(j,k)为相空间中所有下标满足k+(j-1)τ＝i的元素的集合，Ck为个数。这样就把确定性成分和非确定性成分分离，从而可以去掉随机干扰项。具体的，在步骤(1)得到确定性成分后，对数据进行如下处理，以得到第一融合数据的时间序列：将确定性成分以小时为单位取1小时内所有数据的加权均值得到第一融合数据Lhour为新形成的时间序列的长度，按以下方法确定加权均值：设1小时内所有数据范围为b～a，先取1小时内所有数据进行均匀量化，量化电平数为N，量化间隔为Δν＝(b-a)/N，令ωi为数据落入在第i区间的数目，则：ykhour=1M×Σj=1MωiΣi=1Nωi×xj---(8)]]>其中，xj为数据，M表示1小时内数据的个数。具体的，步骤(3)中，构建IHSSM模型的步骤是：确定挠度日温度效应的周期为24小时；令Ldaily＝24M，M为整数值，对时间序列建立IHSSM模型，IHSSM模型为：yk=μk+γk+ϵkμk+1=μk+νk+ξk+1νk+1=νk+ζk+1δk=δk-1+βk-1+ωkβk=βk-1+μk,ϵk~N(0,σϵ2)ξk~N(0,σξ2)ζk~N(0,σζ2)ωk~N(0,Ωs)μk~N(0,σμ2)---(9)]]>其中，μk为趋势成分；νk为体现了其中斜率成分的变化量；βk为季节趋势成分；δk是k时刻的季节波动；γk为随机虚拟变量形式；εk、ωk、ζk、ξk、μk为k时刻各种分量相应的干扰成分；将IHSSM模型写为状态空间形式：yk=Zkαk+ϵkαk+1=Tαk+Rηk+1---(10)]]>其中，各个变量定义的矩阵如下：αk=μkνkδkβ‾k(2s+2)×1,ηk=ξkζkωkμk(2s+2)×1,T=1101×s01×s0101×s01×s0s×10s×1Is×sWs×s0s×10s×10s×sIs×s(2s+2)×(2s+2).]]>优选的，在进行Kalman滤波前采用EM算法估计Kalman滤波的各种参数，EM分为E步和M步，E步计算出上一期迭代得到的参数估计结果导致的隐变量的当期值，以及由当期值决定的当期迭代所需的似然函数的期望，M步是使该期望最大化，得到被估计参数当期迭代的估计结果，步骤为：(3-1)设γ＝[γ1,γ2,…,γT]为不完全观测数据，β＝[β1,β2,…,βT]为缺失数据，记完全数据似然函数表示为：L(θ|γ,β)＝p(γ,β|θ)(11)其中p(γ,β|θ)为联合密度函数，θ是要求取的参数，给定θ0为其初始值；(3-2)给定未知参数的当前估计θk-1：Q(θ,θk-1)=Eθk-1[logp(γ,β|θ)]---(12)]]>(3-3)取θ的最大化：θk=argmaxθQ(θ,θk-1)---(13)]]>通过以上迭代求得θ值；应用Kalman滤波算法，通过预测和校正计算，计算出αk的校正值，从而应用IHSSM模型分离出第一季节项和第一趋势项这里是由于αk中含有季节项、趋势项等，意味着Kalman滤波算法实质是对季节项、趋势项进行计算，从而可以将季节项、趋势项进行分离。优选的，步骤(4)中，将分离出的第一趋势项以天(24小时)为单位，取1天内的所有数据取加权均值得到第二融合数据Lannual为新形成的时间序列的长度。具体的，步骤(5)中，以旬为单位将1年的数据分成36个片段，确定挠度年温度效应的周期为36；从每个片段的相同位置取1个数组成时间序列i是指片段中第i个数据，Ls是指片段的个数；对每组构建IHSSM模型，分离出第二趋势项和第二季节项然后将每组分离出的第二趋势项和第二季节项组合成第三趋势项和第三季节项从而得到需要的挠度年温度效应和长期挠度。更进一步的，如果片段的个数少于11，则将末尾的数据重复构成虚拟数据。本发明与现有技术相比，具有如下优点和有益效果：1、本发明通过多次应用IHSSM模型对信号进行分离，分离出日温度效应、年温度效应和长期挠度。解决了桥梁健康监控系统中挠度测量各组成成分的分离问题，精确获取挠度监测信号各响应分量，为正确诊断桥梁结构病害、准确评估其工作状态，以及分析病害发生机理提供基础。2、本发明基于桥梁挠度数据量大以及计算实时性要求，将桥梁挠度信号进行分段处理，从而处理速度较快。3、本发明利用局部切空间排列方法将挠度信号的随机干扰项去除，使得分离结果更加准确。4、本发明根据挠度数据的时间特点，对挠度数据进行数据融合处理，此方法可以减少计算量，提高计算效率。附图说明图1是本实施例所采用潭洲大桥立面图；图2为实例中实测挠度数据；图3为所有模拟挠度组成的混合模拟挠度时程曲线；图4(a)为混合后的挠度数据；图4(b)为图4(a)中一段数据的局部放大图；图5(a)为去掉随机干扰成分后的数据图；图5(b)为以小时为单位取加权均值的融合数据图；图6(a)为分离的挠度日温度效应季节项；图6(b)为分离的挠度日温度效应趋势项；图6(c)为分离的挠度日温度效应季节项和实际值的对比图，其中实线为季节项，虚线表示实际值；图7(a)为分离的桥梁挠度年温度效应季节项；图7(b)为分离的桥梁挠度年温度效应季节项和实际值的对比图，其中实线为季节项，虚线表示实际值；图8(a)为分离的桥梁挠度年温度效应趋势项；图8(b)为分离的桥梁长期挠度和实际值的对比图，其中实线为趋势项，虚线表示实际值；图9为本实施例方法的流程图。具体实施方式下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。实施例1为了说明本发明一种桥梁挠度温度效应和长期挠度的分离方法的具体步骤，本实施例以广东佛山市潭州大桥扩建桥为例进行具体说明。为了获取桥梁结构真实的挠度信号，对广东佛山市潭州大桥扩建桥进行连续48小时的现场挠度监测。潭洲大桥位于佛山莲塘水闸下游的潭洲水道，该桥扩建桥梁主桥采用75m+125m+75m预应力混凝土连续刚构箱梁桥(见图1)，桥梁宽14.25m(包括1.75m人行道)，箱梁采用单箱单室截面，墩身采用薄壁空心墩，墩身截面采用单箱单室结构，墩身纵桥向宽2.8m，横桥宽7.25m。设计荷载：公路-Ⅰ级；设计速度：120km/h。挠度监测采用BJQN-5B型动挠度仪，分辨率为测量量程的1‰，测量精度为±0.02mm，试验时实际采样频率为10Hz。挠度实测数据如图2所示。由于该桥建成后尚未通车，且监测时间相对较短，挠度监测结果中可以忽略混凝土徐变收缩等产生的影响，认为挠度主要由环境温度变化以及环境噪声所引起，即将所测数据看作S1(k)。以一座三跨预应力砼连续刚构桥为背景桥梁，采用有限元进行仿真分析，获取挠度的年温度效应和长期挠度的模拟数据。背景桥跨径组合为65m+100m+65m，预应力砼连续刚构体系。采用Midas软件计算主桥中跨挠度值,取年温度为35oC，f＝0.75因年温度为周期性函数，假设其按正弦变化，则可得到按时序变化的年温度效应：S2(k)=17.5×f×sinπk4380]]>其中：k为取样时间，S2(k)的单位为mm。假设长期挠度由混凝土收缩徐变因素导致，采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62-2004)可计算该桥梁收缩徐变效应S3(k)。图3为所有模拟挠度组成的混合模拟挠度时程曲线。将实测的挠度信号和挠度模拟信号相加，形成待分离挠度信号，其原因有两个：一方面是长期挠度(趋势项)的形成需要的时间很长，目前桥梁监控系统使用的时间有限，所以只好用模拟数据来替代实际值；另一方面，将实测的挠度信号和挠度模拟信号相加形成待分离挠度信号，可以将分离结果和各个分量进行比较，确认分离的效果。混合后的信号如图4(a)所示，其局部放大图如图4(b)所示。结合图9，对混合后的信号，进行如下处理：步骤1：先对挠度数据进行分段处理。因为挠度日温度效应的周期可认为是24小时，因此采用局部切空间排列方法对48小时内时间序列的确定性成分与随机成分进行分离，去掉随机干扰成分后的数据图如图5(a)所示。再以小时为单位以取加权均值的方式对数据进行融合，融合数据图如图5(b)所示。假设挠度数据总长度为Lsecond(单位：秒)，以小时为单位对采集的挠度数据进行数据融合：1)首先采用局部切空间排列方法(LocalTangentSpaceAlignment，LTSA)对48小时内时间序列的确定性成分与随机成分进行分离：①首先把序列S(k)在高维空间重构，当相空间嵌入维数为m时：S(k)＝f(S(k-m),S(k-m+1),…,S(k-1))对时间序列相空间重构可得：p(j,k)＝S(k+(j-1)τ)τ为时间延迟。②局部邻域构造：取上式组成的时间序列相空间样本点，为方便记为xi，求样本点的邻域Xi＝[xi1,xi2,…,xik]，Xi为xi包括自身在内的k个临近点构成的集合。③局部坐标线性拟合：对Xi中心化，得为邻域数据均值，其中ek为k维单位向量。对进行SVD分解，记其中Λi为奇异值按降序排列的对角阵。④局部坐标系统的排列。构造其中Si是满足[x1,x2,…,xL]Si＝[xi1,xi2,…,xik]的选择矩阵，L为样本点数目，计算B对应的最小d+1个特征值对应的特征向量t1,t2,…,td+1，则T＝[t2,t3,…,td+1]即为整个样本的低维空间流形。⑤把得出的低维空间流形坐标映射回原时间序列相空间：yi=x‾i+QiLi(ti-ti‾)]]>其中：Li为Xi到T的转化矩阵。随机成分为：σi＝xi-yi然后通过下式分别把yi、σi映射到一维时间序列：S^(k)=Σt∈{Ii(j,k)}ytCk]]>σ^(k)=Σt∈{Ii(j,k)}σtCk]]>其中Ii(j,k)为相空间中所有下标满足k+(j-1)τ＝i的元素的集合，Ck为个数。这样就把确定性成分和非确定性成分分离，从而可以去掉随机干扰项。2)将确定性成分以小时为单位取1小时内所有数据的加权均值得到第一融合数据的时间序列Lhour为新形成的时间序列的长度，按以下方法加权均值：设1小时内所有数据范围为b～a，先对1小时内所有数据进行均匀量化，量化电平数为N，量化间隔为Δν＝(b-a)/N，令ωi为数据落入在第i区间的数目，则ykhour=1M×Σj=1MωiΣi=1Nωi×xj]]>其中，xj为数据，M表示1小时内数据的个数。步骤2：确定挠度日温度效应的周期为24小时；令Ldaily＝24M(M为整数值)，对时间序列建立IHSSM模型，从中提取挠度日温度效应和趋势项。IHSSM模型为：yk=μk+γk+ϵkμk+1=μk+νk+ξk+1νk+1=νk+ζk+1δk=δk-1+βk-1+ωkβk=βk-1+μk,ϵk~N(0,σϵ2)ξk~N(0,σξ2)ζk~N(0,σζ2)ωk~N(0,Ωs)μk~N(0,σμ2)]]>其中，μk为趋势成分；νk为体现了其中斜率成分的变化；βk为季节趋势成分；δk是k时刻的季节波动；γk为随机虚拟变量形式；εk、ωk、ζk、ξk、μk为k时刻各种分量相应的干扰成分。将IHSSM模型写为状态空间形式：yk＝Zkαk+εkαk+1＝Tαk+Rηk+1其中，各个变量定义的矩阵如下：αk=μkνkδkβ‾k(2s+2)×1,ηk=ξkζkωkμk(2s+2)×1,T=1101×s01×s0101×s01×s0s×10s×1Is×sWs×s0s×10s×10s×sIs×s(2s+2)×(2s+2).]]>将时间序列表示成状态空间形式后，可以利用EM算法估计Kalman滤波的各种参数。EM分为E步和M步，E步计算出上一期迭代得到的参数估计结果导致的隐变量的当期值，以及由当期值决定的当期迭代所需的似然函数的期望，M步是使该期望最大化，得到被估计参数当期迭代的估计结果。①设γ＝[γ1,γ2,…,γT]为不完全观测数据，β＝[β1,β2,…,βT]为缺失数据，记完全数据似然函数表示为L(θ|γ,β)＝p(γ,β|θ)(6)其中p(γ,β|θ)为联合密度函数。θ是要求取的参数，给定θ0为其初始值。②给定未知参数的当前估计θk-1Q(θ,θk-1)=Eθk-1[logp(γ,β|θ)]---(7)]]>③取θ的最大化θk=argmaxθQ(θ,θk-1)---(8)]]>通过以上迭代可以求得θ值。应用Kalman滤波算法，通过预测和校正计算，计算出αk的校正值，由于αk中含有季节项、趋势项等，也就意味着Kalman滤波算法实质是对季节项、趋势项进行计算，从而可以将季节项、趋势项进行分离。分离结果如图6所示。图6(a)表示分离的挠度日温度效应季节项，图6(b)表示分离的挠度日温度效应趋势项，图6(c)表示分离的挠度日温度效应季节项和实际值的对比图。将趋势项以天(24小时)为单位取1天内的所有数据的按上面的方法取加权均值得到Lannual为新形成的时间序列的长度。步骤3：在分段分离挠度日温度效应后，再对分离出来的数据再以1天(24小时)为单位取加权均值进行数据融合，形成新的数据。步骤4：以旬为单位将1年的数据分成36个片段，确定挠度年温度效应的周期为36。从每个片段的相同位置取1个数组成时间序列i是指片段中第i个数据，Ls是指片段的个数，如果片段的个数少于11，则将末尾的数据重复构成虚拟数据(比如可以虚构的2月31日的数据，数据值等于2月28日或29日的实际数据值，1月31日和虚构的2月31日可以组成1组)。对每组构建IHSSM模型，共分离11次，分离出趋势项和季节项然后将每组分离出的趋势项和季节项组合成和(其中虚构的数据分离出的趋势和季节项可以省略)，此结果即是需要的挠度年温度效应和长期挠度，如图7和8所示。图7(a)表示分离的桥梁挠度年温度效应季节项，图7(b)表示分离的桥梁挠度年温度效应季节项和实际值的比对示意图，图8(a)表示分离的桥梁挠度年温度效应趋势项，图8(b)表示分离的桥梁长期挠度和实际值的比对示意图。上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受上述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。当前第1页1 2 3