一种基于Hadoop的自适应RK‑means算法的制作方法

本发明属于数据挖掘技术领域，涉及一种基于Hadoop的自适应RK-means算法。

背景技术：

K-means算法是数据挖掘中应用最经典的聚类算法，具有实现过程简单，并且收敛速度快等优点，但是由于初始聚类中心选择对聚类结果影响较大，K-means算法具有很强敏感性，针对PB集数据串行化处理方式的效率也很低。为此，许多学者采用了自适应选取聚类中心的K-means算法，实现了聚类数目的自适应选取，但是聚类中心点并不是全局最优，有的采用了面向全局优化的K-means算法，只能实现聚类数目的随机性选取，不能保证聚类数目的准确性。传统算法采取的串行化程序思想限制了对大数据的处理效率。

由于K-means算法能够实现基于MapReduce的并行K-means处理方式，本发明提出了将自适应初始聚类中心选取算法与RK-means算法相结合起来，并且在Hadoop平台下实现了自适应RK-means算法，不但保证了聚类中心数目的准确获取，而且保证了聚类中心的全局最优，在提高聚类结果的准确性的同时，也提升了算法的运行效率。

技术实现要素：

有鉴于此，本发明的目的在于提供一种基于Hadoop的自适应RK-means算法，该方法针对传统K-means算法对初始聚类中心选择的敏感、不具备全局优化能力，并且运行效率低下的问题，将自适应初始聚类中心选取算法与RK-means算法相结合，并且在Hadoop平台下实现了自适应RK-means算法，不但保证了聚类中心数目的准确获取，而且保证了聚类中心的全局最优。

为达到上述目的，本发明提供如下技术方案：

一种基于Hadoop的自适应RK-means算法，包括以下步骤：

S1：根据业务需求，输入待聚类的数据集；

S2：运用基于Hadoop的自适应聚类中心算法获取聚类中心点及数目；

S3：将上一步的结果作为算法的初始聚类中心，输入到基于Hadoop的RK-means算法中，获取全局最优的聚类簇；

S4：输出聚类结果。

进一步，所述步骤S1具体包括：

S11：确定业务需求；

S12：根据业务需求准备数据；

S13：数据预处理；

S14：得到待聚类的数据集。

进一步，所述步骤S13中的数据预处理通过分析数据、异常值处理、数据的抽取及数据的转换，直接作为算法的输入数据。

进一步，所述步骤S2具体包括：

S21：将数据集X读入，估计数据集内随机观测值的空间距离，按照升序排列，随机选取一观测点作为初始中心点，聚类数目设置为1，设定两观测值相似性阈值；

S22：估计其余观测点与初始聚类中心间的空间距离，将观测点的id作为map函数的key，观测点与初始聚类中心点的空间距离设为value输出到Combine函数中；

S23：Combine函数选取所有观测点中最小的空间距离，取该距离与两观测值相似性阈值进行比较：若偏大，则聚类数量进1，将该观测值的id作为key，该观测值的属性记为value输出到Reduce中；若偏小，则将初始中心点的id作为key，该观测值的属性记为value输出到Reduce；

S24：通过Reduce函数更新两观测值相似性阈值；

S25：判断数据集中所有数据是否都已分类完毕：若是，则输出聚类中心；反之，则重复执行S22至S24。

进一步，所述步骤S3具体包括：

S31：根据每个对象到初始聚类中心的距离，将对象分配给最近的聚类中心；

S32：Map函数中，key表示该类簇所属聚类中心类别，value表示类别及其对象的属性；

S33：Reduce函数读取Map函数写入的中间结果，即context.write(key，value)；

S34：获取每个簇的平均值；

S35：根据各对象到每个簇中心的距离，采用增加随机项的更新算法更新聚类中心，将它们重新分配给距离最近的簇；

S36：输出不同的簇，其中key为各个簇的编号，value为各个簇中每个对象对应的属性，最后的输出就是RK-means聚类的结果

本发明的有益效果在于：本发明将自适应初始聚类中心选取算法与RK-means算法相结合起来，并且在Hadoop平台下实现了自适应RK-means算法，不但保证了聚类中心数目的准确获取，而且保证了聚类中心的全局最优，在提高聚类结果的准确性的同时，也提升了算法的运行效率。

附图说明

为了使本发明的目的、技术方案和有益效果更加清楚，本发明提供如下附图进行说明：

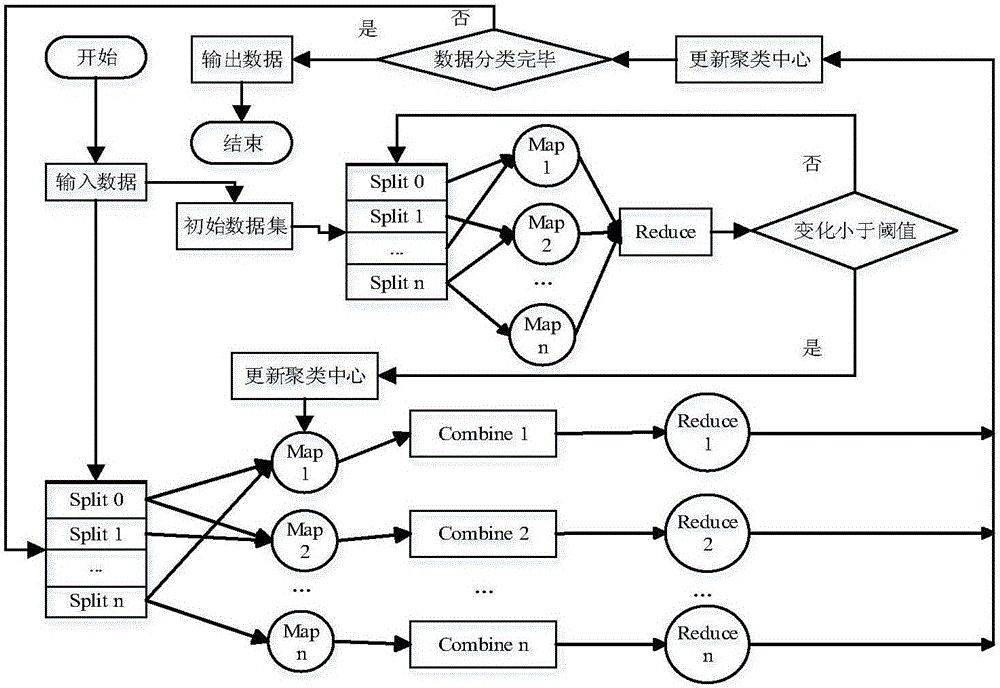
图1为本发明实施流程图；

图2为本发明算法框架图。

具体实施方式

下面将结合附图，对本发明的优选实施例进行详细的描述。

图1为本发明实施流程图，如图所示，该算法包括以下步骤：S1：根据业务需求，输入待聚类的数据集；S2：运用基于Hadoop的自适应聚类中心算法获取聚类中心点及数目；S3：将上一步的结果作为算法的初始聚类中心，输入到基于Hadoop的RK-means算法中，获取全局最优的聚类簇；S4：输出聚类结果。

图2为本发明算法框架图，实施例如下：

1、自适应选取初始中心选取算法实现

算法思想：假设用户群数目为N_s，样本数据集X＝{x_i|i＝1,2,...,n}，C_j(j＝1,2,...,k)表示k个聚类簇，聚类中心为c_j(j＝1,2,...,k)，两个不同对象间不相似的阈值设为ε，自适应初始中心选取的准则为：若d(x_i,c_i)＞ε，其中那么x_i不属于C_j类。

算法步骤：

Step 1：输入X＝{x_i|i＝1,2,...,n}的用户数据集；

Step 2：计算数据集内随机对象x_i,x_j间的空间距离D(x_i,x_j)，按照升序排列后放入数据集D；

Step 3：从数据集中随机选取一个对象作为初始聚类中心，设聚类数目为k＝1，两观测值相似性阈值取为

Step 4：估计数据集内其余对象与初始聚类中心间的空间距离，选出极小值与进行比较，若大于则聚类数量增加1，从而获得更新的聚类中心；若小于则将此点与对应的聚类中心归为一类，同时更新相似性阈值

Step 5：重复执行Step 4，直到数据集中所有对象分类完毕；

Step 6：输出聚类中心。

2、RK-means算法实现

聚类中心处于该类簇所有对象的中心位置，如果更新后的聚类中心距离其余对象很远，那么该聚类中心是一个没有实际意义的聚类中心，聚类质量很差。为此，RK-means算法在对聚类中心进行更新时，增加了一个与数据集的几何中心距离、以及初始聚类中心距离相关的随机项，保证每次更新的聚类中心距离簇中对象相对较近，偏差较少，从而提升算法的探索能力，以下给出RK-meanns算法的聚类中心更新方程。

假设算法到t-1步时，k个簇依次表示为C₁(t-1)，C₂(t-1)，C₃(t-1)，…，C_k(t-1)，则RK-means算法更新聚类中心的方程表示为：

其中，r是D维的随机变量，服从D维的超立方体[0,1]^D上均匀分布，a(t)是增加随机项的系数因子；随机变量r与(m-m_j(t-1))之间的乘积为两向量之间的点积；m是x₁,x₂,x₃,...,x_n的算术平均，代表数据集的几何中心。

可以看出，随机变量r增加了算法在迭代过程中的随机性，能够跳出传统K-means算法容易陷入局部最优的缺陷，使得算法具有全局探索的能力。因此，式(m-m_j(t-1))提高了算法迭代更新解的质量，若由m_j得到的当前聚类中心m₁(t),m₂(t),...,m_n(t)没有t-1步骤的聚类中心好，则不修正t-1步骤的聚类中心，往后执行t+1步，这样就可以保证算法在迭代过程具有较好的探索方向。

此外，RK-means算法中设置了随着迭代次数t的增加线性地减小的因子a(t)。在迭代初期a(t)较大，对聚类中心点更新的变化范围较大，算法的全局探索能力较强；在迭代后期a(t)较小，算法的局部搜索能力很强。假设最大迭代次数为GN，设a(t)最小值为a₀，最大值为a₁，则

RK-means算法步骤：

Step 1：将自适应选取初始中心选取算法中获取的k个聚类中心m₁(0),m₂(0),...,m_k(0)，作为RK-means算法的初始聚类中心；

Step 2：根据每个对象到初始聚类中心的距离，将其分配到离它最近的聚类中心所在的类中，k个聚类分别表示为C₁(t-1)，C₂(t-1)，C₃(t-1)，…，C_k(t-1)；

Step 3：按RK-means算法的聚类中心更新方程m_j更新聚类中心，得到新的聚类中心表示为m₁(t)，m₂(t)，…，m_k(t)；

Step 4：首先，计算出总类间离散度F(t)＝F(m₁(t),m₂(t),...,m_k(t))，若该值大于t-1步中得到的总类间离散度，则不更新聚类中心，令t＝t+1，转到Step 2继续进行迭代。若F(t-1)与F(t)的差别小于正数ε，或者算法达到了迭代次数上限的t＝GN，迭代结束；否则令t＝t+1，转到Step 2继续迭代。

最后说明的是，以上优选实施例仅用以说明本发明的技术方案而非限制，尽管通过上述优选实施例已经对本发明进行了详细的描述，但本领域技术人员应当理解，可以在形式上和细节上对其作出各种各样的改变，而不偏离本发明权利要求书所限定的范围。