一种适用于嵌入式系统的Montgomery模乘计算方法与流程

本发明涉及公钥密码体制领域，具体地说，涉及一种适用于嵌入式系统的montgomery模乘计算方法。

背景技术：

1985年，p.l.montgomery提出了montgomery模乘算法，它是现在应用最广泛的一种模乘算法。其基本思想是用简单省时的加法和移位操作代替费时的求逆和除法操作。对于计算模乘p＝a*bmodn(a,b,n为n比特的二进制大整数且0<a,b<n)，该算法首先选取一个与n互素的整数r(一般取r＝2ⁿ)，将模n的乘法运算转化为模r的乘法运算。下面我们定义montgomery乘积：monpro(a,b)＝a*b*r^-1modn。

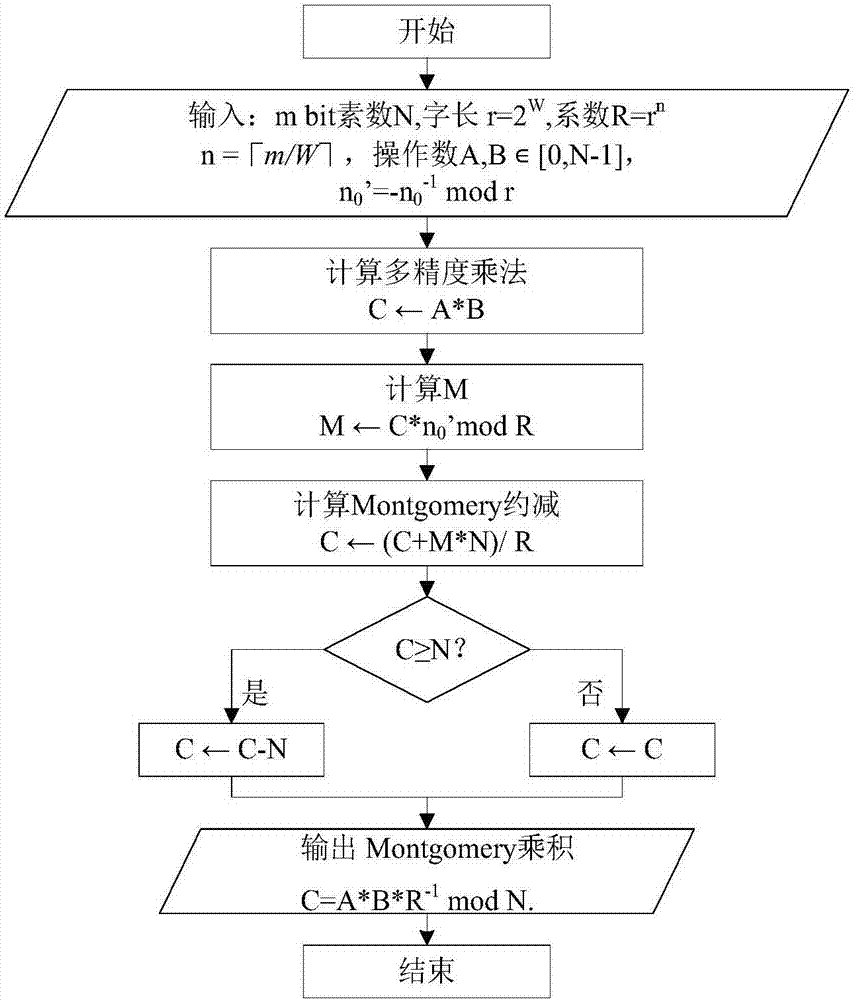
montgomery模乘算法的计算结构见图1所示，具体分为以下三个步骤：

(1)计算a，b的n剩余类：a’＝a*rmodn＝a*r²*r^-1modn＝monpro(a*r²),

b’＝b*rmodn＝b*r²*r^-1modn＝monpro(b*r²)；

(2)计算a’和b’的montgomery乘积p’＝a’*b’*r^-1modn＝monpro(a’,b’)；

(3)将p’转化为模乘乘积p，p＝a*bmodn＝a’*r^-1*b’*r^-1modn

＝p’*r^-1modn＝monpro(p’)。

因此，montgomery模乘算法的核心是计算montgomery乘积monpro(a’,b’)，其具体算法流程描述见图2所示。从图2中可以看出montgomery乘积计算可以分为两个关键步骤：计算多精度乘法t←a*b和计算montgomery约减p←(t+m*n)/r。

1990年dusse提出采用r进制数的montgomery模乘算法，并利用n0’＝-n0^-1modr代替n’对算法进行了相应的改进。1996年koc对各种montgomery模乘算法的实现方法进行了分析总结，并归纳了5种主要的改进montgomery算法：sos、cios、fios、fips和cihs。其中后两位字母os/ps/hs表示计算乘法扫描方式，os表示操作数扫描，ps表示乘积扫描，hs表示混合扫描；而前面的字母s/ci/fi表示多精度乘法和montgomery约减两部分使用的集成方式，s表示分离的方式即完全计算完一部分之后再计算另一部分，ci表示粗粒度集成方式即粗粒度交替计算两部分，fi表示细粒度集成方式即细粒度交替计算两部分。这些算法的实现都可以由一系列操作：乘法mul，加法add，加载load，存储store等实现。所以高性能的实现算法主要集中在优化这些操作上面。在嵌入式系统中，由于可用寄存器的数量有限，load/store等存储操作显得尤为重要，目前常用的方法中，使用的寄存器数量固定，一般分为使用5个寄存器和n+4(n为模n包含字数的大小)个寄存器两种方式。使用寄存器比较少(5个)的方法需要较多的内存存取操作，而使用寄存器较多的方式(n+4)需要的内存存取操作较少但常常因为所需寄存器数量超过处理器可用寄存器数量而不能使用。因此如何通过处理器可用寄存器数量和n的大小动态的使用寄存器，使得通过充分利用寄存器来减少内存存取操作的数量成为当前需要解决的问题。

技术实现要素：

本发明的目的在于克服目前montgomery模乘算法不适用于资源较少的嵌入式系统的缺陷，为了提高montgomery模乘算法的计算效率，提出了一种粗粒度集成的混合扫描方式计算montgomery模乘的方法，该方法充分利用处理器的可用寄存器数量动态选取d，通过在块内操作数扫描时共享操作数减少操作数读取数目，通过在块间乘积扫描时每列计算完所有乘积后存在2d+1个寄存器中来减少中间结果的存取数目，整体上减少了内存存取数目，提高了算法实现效率。

为了实现上述目的，本发明提供了一种适用于嵌入式系统的montgomery模乘计算方法，所述方法包括：多精度乘法和montgomery约减；对于多精度乘法和montgomery约减两部分均采用混合扫描的方式进行计算，内部循环使用操作数扫描的方式，外部循环使用乘积扫描的方式；而多精度乘法和montgomery约减两部分之间使用粗粒度集成的方式，即两部分交替计算。

上述技术方案中，所述方法具体包括：

步骤1)设大数n是m比特素数，处理器的字长是w比特，则n的字数大小是a,b是两个n剩余类即0<a,b<n；montgomery系数r＝2^nw，n0’＝-n0^-1modr，n0为n的最低位；选择d，d是内部循环的字数大小；则外部循环的大小是为取大于等于其的最小整数运算；

步骤2)a与b的模乘计算过程为：c＝a*b，m＝c*n0’modr，c＝(c+m*n)/r；将操作数a、b、m、n、c的每d个字作为一个整体：

e＝(e[r-1],…,e[0])＝({a[n-1],a[n-2],….,a[n-d]}…{a[d-1],a[2],a[1],a[0]})

f＝(f[r-1],…,f[0])＝({b[n-1],b[n-2],….,b[n-d]}…{b[d-1],b[2],b[1],b[0]})

g＝(g[r-1],…,g[0])＝({m[n-1],m[n-2],….,m[n-d]}…{m[d-1],m[2],m[1],m[0]})

h＝(h[r-1],…,h[0])＝({n[n-1],n[n-2],….,n[n-d]}…{n[d-1],n[2],n[1],n[0]})

q＝(q[2r-1],q[2r-3],…,q[1],q[0])＝({c[2n-1],c[2n-2],c[2n-3],c[2n-d]},…,

{c[d-1],c[2],c[1],c[0]})

依次计算第q，0≤q≤2r-1列的所有部分乘积：

e[k]*f[l]+g[k]*h[l]＝(q[q+1],q[q])，

其中k+l＝q；直到所有列数计算完成，得到c；

步骤3)判断c≥n是否成立，如果成立，令c＝c-n；转入步骤4)，否则，转入步骤4)；

步骤4)输出a与b的montgomery乘积结果c。

上述技术方案中，所述步骤2)具体包括：

步骤2-1)令q＝0；

步骤2-2)将所有满足k+l＝q的k，l的集合记为a：a＝{k,l|k+l＝q}；

步骤2-3)计算(q[q+1],q[q])＝∑ae[k]*f[l]；

其中，

e[k]*f[l]＝(a[kd+3],a[kd+2],a[kd+1],a[kd])*(b[ld+3],b[ld+2],b[ld+1],b[ld])；

步骤2-4)判断q<r是否成立，如果判断结果是肯定，则计算g[q]＝q[q]*n0’；否则，转到步骤2-5)；

步骤2-5)计算(q[q+1],q[q])＝(q[q+1],q[q])+∑ag[k]*h[l]；

步骤2-6)令q＝q+1；若q小于等于2r-2，令k＝k+1，返回步骤2-2)；否则，转入步骤2-7)；

步骤2-7)计算第q列c＝c/r，由于r＝2^nw，所以：

c＝(c[2n-1],c[2n-2],…,c[n+1],c[n])。

与现有技术相比，本发明的技术优势在于：

使用粗粒度集成的方式将混合扫描思想应用于montgomery模乘计算中，通过动态选取d合理利用操作数，减少嵌入式系统中内存存取数量，提高montgomery模乘算法实现效率。

附图说明

图1是现有的montgomery模乘计算结构示意图；

图2是现有的montgomery模乘计算montgomery乘积的流程图；

图3是本发明的模乘计算方法的示意图；

图4是本发明的粗粒度集成乘积和操作数混合扫描的montgomery模乘方法cipohs-a(n＝8,d＝4)结构图；

图5是本发明的粗粒度集成乘积和操作数混合扫描的montgomery模乘方法cipohs-b(n＝8,d＝3)结构图；

图6本发明的方法中分块乘积扫描的示意图。

具体实施方式

下面结合附图和具体实施例对本发明的方法做进一步详细的说明。

一种适用于嵌入式系统的montgomery模乘计算方法，所述方法包括：

步骤1)设大数n是m比特素数，处理器的字长是w比特，则n的字数大小是a,b是两个n剩余类即0<a,b<n；montgomery系数r＝2^nw，n0’＝-n0^-1modr，n0为n的最低位；选择d，d是内部循环(使用操作数扫描)的字数大小；则外部循环(使用乘积扫描)的大小是为取大于等于其的最小整数运算；

步骤2)计算a与b的模乘结果c，计算过程为：

1)c＝a*b；

2)m＝c*n0’modr；

3)c＝(c+m*n)/r.；

如图3所示，将a,b表示2个m比特的多精度整数，为：a＝(a[n-1],…,a[2],a[1],a[0])，b＝(b[n-1],…,b[2],b[1],b[0])。则乘积c＝a·b可以表示为：c＝(c[2n-1],…,c[2],c[1],c[0])。

将操作数a、b、m、n、c的每d个字作为一个整体，在本实施例中，n＝8,d＝4；表示如下：

e＝(e[1],e[0])＝({a[7],a[6],a[5],a[4]}{a[3],a[2],a[1],a[0]})

f＝(f[1],f[0])＝({b[7],b[6],b[5],b[4]}{b[3],b[2],b[1],b[0]})

g＝(g[1],g[0])＝({m[7],m[6],m[5],m[4]}{m[3],m[2],m[1],m[0]})

h＝(h[1],h[0])＝({n[7],n[6],n[5],n[4]}{n[3],n[2],n[1],n[0]})

q＝(q[3],q[2],q[1],q[0])＝({c[15],c[14],c[13],c[12]}{c[11],c[10],c[9],c[8]}

{c[7],c[6],c[5],c[4]}{c[3],c[2],c[1],c[0]})

则计算c＝a*b可以转化为计算(q[3],q[2],q[1],q[0])＝(e[1],e[0])*(f[1],f[0])

计算m＝c*n0’modr可以转化为计算(g[1],g[0])＝(q[1],q[0])*n0’

计算c＝c+m*n可以转化为计算

(q[3],q[2],q[1],q[0])＝(q[3],q[2],q[1],q[0])+(g[1],g[0])*(h[1],h[0]))

下面使用乘积扫描方式交替计算c＝a*b和c＝c+m*n(m＝c*n0’modr)。即计算完第q列，0≤q≤2r-1列的所有部分乘积：

e[k]*f[l]+g[k]*h[l]＝(q[q+1],q[q])(其中k+l＝q)后，再计算下一列，直到所有列数计算完成。

算法结构描述见图4所示，图中菱形结构中的每一个阴影块①，②等和乘法结构中的每一个大的方框都表示一个乘积e[k]*f[l]或g[k]*h[l]。计算整个菱形结构时以阴影块为基本单位，则其规模大小为r＝n/d＝2；块之间计算时采用粗粒度乘积扫描方式，先计算第0列的所有e[k]*f[l](即块①)，计算所有g[k]*h[l](即块②)；再计算第1列的所有e[k]*f[l](即块③，④)，计算所有g[k]*h[l](即块⑤，⑥)；最后计算第2列的所有e[k]*f[l](即块⑦)，计算所有g[k]*h[l](即块⑧)。

对于计算图中的每一个阴影块①，②等，即计算每一个e[k]*f[l](或g[k]*h[l])，其采用操作数扫描的方式，规模大小是d＝4；按照行的方式进行计算，每行中保持一个操作数b[i]不变，与另一个操作数a[j](0≤j<d)的所有项相乘；计算完这行的所有乘积后再计算下一行。

在另一实施例中，当n＝8,d＝3时，如图5所示，将整个乘法分成许多个块①，②等，而在这些块之间也依然使用粗粒度集成的乘积扫描方式即按图中序号顺序①-进行执行，规模大小是由于不能被整除，分成的块不都是完整的块，如图4中块①是一个完整的d*d的块，块⑦是一个不完整的块。下面我们根据块的完整性，可以将乘积扫描的所有列分成三部分：第一部分是第1到r-1列，所有的块都是完整块，大小是d*d；第二部分是第r到2r-2列，其最上面和最下面的块是不完整的块，大小是[d-(rd-n)]*d，剩下的块都是完整块大小是d*d；第三部分即2r-1列，包含两个不完整块，大小是[d-(rd-n)]*[d-(rd-n)]。块内部仍然使用操作数扫描的方式记性计算，计算不完整的菱形块则是沿着长边进行操作数扫描。

所述步骤2)具体包括：

步骤2-1)令q＝0；

步骤2-2)将所有满足k+l＝q的k，l的集合记为a：a＝{k,l|k+l＝q}；

步骤2-3)计算(q[q+1],q[q])＝∑ae[k]*f[l]；

采用操作数扫描方式：按照行的方式进行计算，每行中保持一个操作数b[i]不变，与另一个操作数a[j](0≤j<d)的所有项相乘；计算完这行的所有乘积后再计算下一行。其中，计算每一个e[k]*f[l]和g[k]*h[l]

如图6所示，

e[k]*f[l]＝(a[kd+3],a[kd+2],a[kd+1],a[kd])*(b[ld+3],b[ld+2],b[ld+1],b[ld])

步骤2-4)判断q<r是否成立，如果判断结果是肯定，则计算g[q]＝q[q]*n0’；否则，转到步骤2-5)；

步骤2-5)计算(q[q+1],q[q])＝(q[q+1],q[q])+∑ag[k]*h[l]；

步骤2-6)令q＝q+1；若q小于等于2r-1，令k＝k+1，返回步骤2-2)；否则，转入步骤2-7)；

步骤2-7)计算第q列c＝c/r，由于r＝2^w，所以：

c＝(c[15],c[14],c[13],c[12],c[11],c[10],c[9],c[8])；

步骤3)判断c≥n是否成立，如果成立，令c＝c-n；转入步骤4)，否则，转入步骤4)；

步骤4)输出a与b的montgomery乘积结果c。

下面根据n/d是否为整数将本发明所述方法分为两种情况：第一种情况是n/d是整数，即我们称之为cipohs-a；第二种情况是n/d不是整数，即我们称之为cipohs-b。对两种方法内存存取的总量进行分析。

1、cipohs-a方法

如图4所示，首先分析每一块内部的内存存取数量：由于每块中使用d+1个寄存器存储操作数，其中d个寄存器存储操作数a，剩下1个寄存器轮流存储操作数b多精度表示的各个字，所以块中每一个操作仅加载一次即可，故每一块中load的数量是2d；而每块的计算结果直接存储在2d+1个寄存器中，所以每块存储中间结果store的数量为0。下面分析外部循环，由于外部循环大小是r＝n/d故共有2r²＝2(n/d)²块，且使用粗粒度集成的乘积扫描方式。在本例中共有2*2²＝8块，块的执行顺序按照图中标注的数字①②③④⑤⑥⑦⑧执行。由于每块load数量是2d，共有2(n/d)²块，故load的总量是2d*2(n/d)²＝4n²/d；而在整个算法中需要存储的是n个字的m(m←c*n0’modr)和n+1个字的最终结果c，故store的总量是n+n+1＝2n+1；所以内存存取(load和store)的总量为4n²/d+2n+1。

2、cipohs-b方法

如图5所示，第一部分：包含前r-1列，所有的块都是完整块如块①、③、④，对于每一块中使用操作数扫描，因此每块中load数量是2d，一共有r*(r-1)块，故load总量是2d*r*(r-1)。第二部分：包含r到2r-2列，每列最上面和最下面的块是不完整块，大小是[d-(rd-n)]*d，在这些块中扫描方式是沿长度为d的方向进行操作数扫描；如图4中块⑦，首先将a[0],a[1],a[2]加载在寄存器中，然后先计算b[6]和a[0],a[1],a[2]的乘积，再计算b[7]和a[0],a[1],a[2]的乘积；故每个不完整块load数量是2d-(rd-n)，共有4(r-1)块。第二部分剩下的块都是完整块，使用正常的操作数扫描，每块load数量是2d，共有(r-2)*(r-1)块。所以这部分load总量是4(r-1)*[2d-(rd-n)]+2d*(r-2)*(r-1)。第三部分：仅仅包含2r-1列，仅包含2个大小为[d-(rd-n)]*[d-(rd-n)]的不完整块，例如块在这些块中按照长度为[d-(rd-n)]的操作数扫描方式进行扫描，故load的数量是4[d-(rd-n)]。表1总结了这三部分load的数量，可以看出load的总量是4rn，而store的数量同cipohs-a相同是2n+1，所以内存存取的总量是4rn+2n+1。

表1

综合cipohs-a和cipohs-b可以将内存存取的总量统一记为下面我们分析koc提出的几种算法和我们提出的cipohs算法的使用寄存器数量和内存存取的数量，如表2所示。

表2

从表2中可以看出，表中比较的几种现有算法中，cios算法的内存存取数量最少需要2n²+3n+1，但是其需要的寄存器数量较多需要n+4个。当n的值比较大时，可用寄存器的数量小于n+4，因此不能再使用这种算法。而cios-5reg和fips算法用到的寄存器数量较小，仅需要5个，但是其内存的存取量比较大。本发明提出的cipohs算法解决了这一问题，它通过可用寄存器的数量动态的选择d，通过合理利用可用寄存器的数量，来减少内存存取的数量。cipohs的内存存取数量是cios的内存存取数量是2n²+3n+1，当d取大于1的整数时，cipohs的内存存取数量小于cios，且d的值越大，cipohs需要的内存存取数量越小。而对于几种算法使用的乘法指令和加法指令等次数基本相同，cipohs算法的内存存取数量最小，所以算法的运算效率最高。

综上所述，本发明的一种适用于嵌入式系统的montgomery模乘计算方法采用粗粒度集成的方式交替计算多精度乘法和montgomery约减两部分，在两部分中使用乘积和操作数混合扫描的方式。通过可用寄存器的数量选择d，充分利用寄存器数量来减少算法内存存取的数量，进一步提高算法的运算效率。

以上所述仅为本发明的具体实施方式，并非用于限定本发明的保护范围，本领域的技术人员应当理解，在不脱离发明原理的前提下，对本发明的技术方案进行修改或者等同替换，都不脱离本发明技术方案的精神和范围，其均应涵盖在本发明的保护范围中。