半潜式钻井平台的壳单元最大等效应力获取方法及装置与流程

本发明涉及海上石油勘探领域，具体而言，涉及半潜式钻井平台的壳单元最大等效应力获取方法及装置。

背景技术：

海洋资源是一种重要的自然资源，常见的海洋资源有海水中生存的生物，溶解于海水中的化学元素，海水波浪、潮汐及海流所产生的能量、贮存的热量，滨海、大陆架及深海海底所蕴藏的矿产资源等等。

为了能够长久和平稳的对海洋资源进行研究和发开，通常会采用在海面上架设钻井平台的方式来使设备和工作人员能够长期的在相对稳定的地点进行工作。钻井平台的种类有很多，比较常见的两种是自升式钻井平台和半潜式钻井平台。

架设钻井平台首要考虑的是安全因素，因此，在设计钻井平台和使用钻井平台的时候，需要判断钻井平台的各种安全指标是否满足要求。如判断钻井平台在实际工作中，其物理结构(如钢材)所受到的等效应力(决定钢材屈服与否的等效应力，即冯·米塞斯应力)是否超过极限值。由于半潜式钻井平台体积庞大，难以通过一个标准的算式直接对其整体的等效应力进行计算，因此首先要采用有限元分析法，将钻井平台划分为大量的壳单元(通常会划分为几十万个壳单元)，进而分别计算每个壳单元的等效应力极值，最后再依据壳单元的等效应力极值来判断钻井平台的安全指标是否符合要求。

下面以一个简单的实例来说明传统的半潜式钻井平台的指定壳单元的等效应力极值是如何计算的。

对于指定的壳单元而言，影响其等效应力的主要因素共有两个，分别是静态荷载和动态荷载，其中，静态荷载有钻井平台自重、钻井平台受到的浮力等；动态荷载主要有波浪力和摇摆力两种。静态荷载通常是稳定的常量，而波浪力和摇摆力则分别会随着波浪相位角(在0°-360°的范围内变化)和摇摆方向(在0°-360°的范围内变化)的变化而变化。因此，实际计算中，为了找到最大的等效应力，需要将静态荷载引起的应力、不同波浪相位角的波浪力以及不同摇摆方向的摇摆力进行组合，以算出不同波浪相位角和不同摇摆方向的情况下，所对应的等效应力。之后从这些计算出的等效应力中选择出数值最大的作为该指定的壳单元的最大等效应力。后续可以按照上述方式找到每个壳单元的等效应力极值。

但使用时发现，传统的计算指定壳单元最大等效应力的方法，其计算量过大，计算时间过长，导致该方法难以在真实的环境中使用。

技术实现要素：

本发明的目的在于提供半潜式钻井平台的壳单元最大等效应力获取方法和装置，以提高实际操作中针对半潜式钻井平台壳单元的最大等效应力的计算效率。

第一方面，本发明实施例提供了半潜式钻井平台的壳单元最大等效应力获取方法，包括如下步骤：

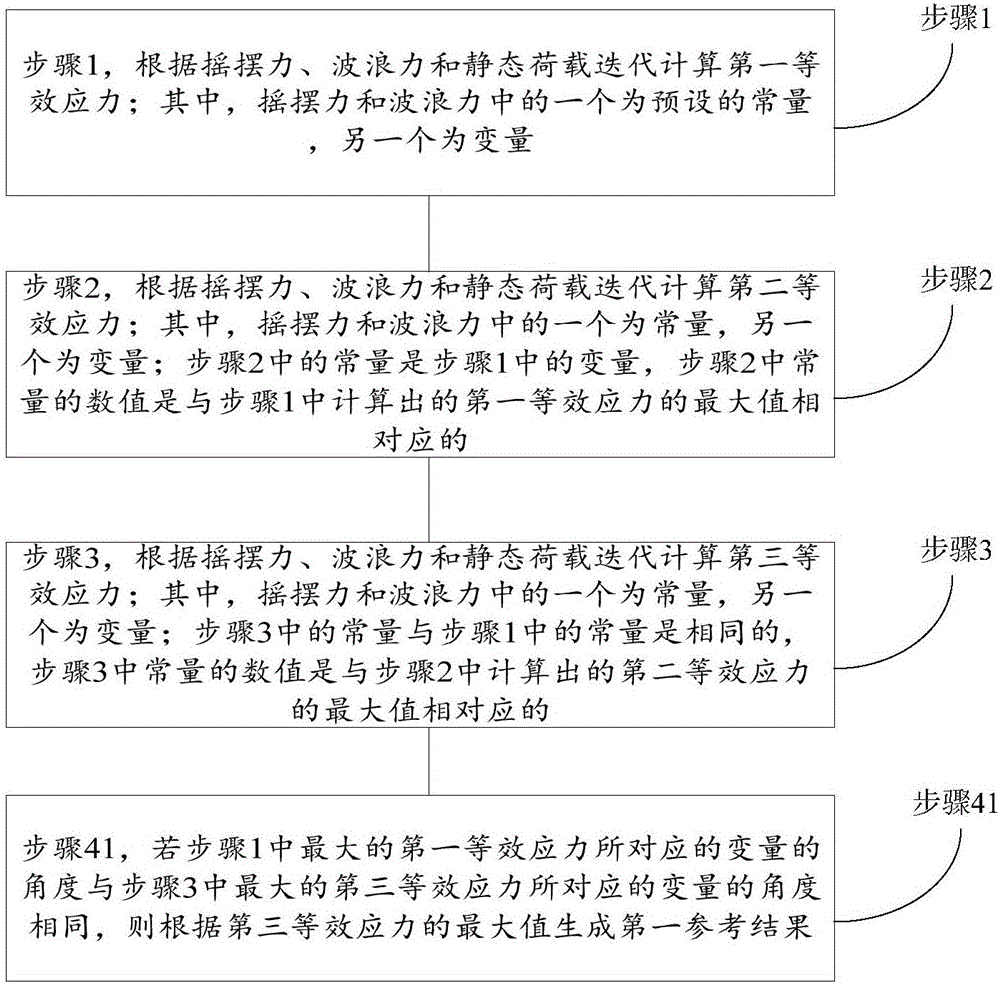
步骤1，根据摇摆力、波浪力和静态荷载迭代计算第一等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；

步骤2，根据摇摆力、波浪力和静态荷载迭代计算第二等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤2中的常量是步骤1中的变量，步骤2中常量的数值是与步骤1中计算出的第一等效应力的最大值相对应的；

步骤3，根据摇摆力、波浪力和静态荷载迭代计算第三等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤3中的常量与步骤1中的常量是相同的，步骤3中常量的数值是与步骤2中计算出的第二等效应力的最大值相对应的；

若步骤1中最大的第一等效应力所对应的变量的角度与步骤3中最大的第三等效应力所对应的变量的角度相同，则根据第三等效应力的最大值生成第一参考结果。

结合第一方面，本发明实施例提供了第一方面的第一种可能的实施方式，其中，该方法还包括如下步骤：

步骤6，根据摇摆力、波浪力和静态荷载迭代计算第六等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；步骤6中的常量与步骤1中的常量是不同的；

步骤7，根据摇摆力、波浪力和静态荷载迭代计算第七等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤7中的常量与步骤6中的常量是不同的，步骤7中常量的数值是与步骤6中计算出的第六等效应力的最大值相对应的；

步骤8，根据摇摆力、波浪力和静态荷载迭代计算第八等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤8中的常量与步骤6中的常量是相同的，步骤8中常量的数值是与步骤7中计算出的第七等效应力的最大值相对应的；

若步骤6中最大的第六等效应力所对应的变量的角度与步骤8中最大的第八等效应力所对应的变量的角度相同，则根据第8等效应力的最大值生成第二参考结果；

判断第一参考结果是否大于第二参考结果；

若是，则输出第一参考结果；

若否，则输出第二参考结果。

结合第一方面的第一种可能的实施方式，本发明实施例提供了第一方面的第二种可能的实施方式，其中步骤3或步骤6中，变量的搜索范围是A-60°～A+60°；其中，A为前一步骤中得到的最大的等效应力所对应的变量的角度。

第二方面，本发明实施例还提供了半潜式钻井平台的壳单元最大等效应力获取装置，包括如下模块：

第一计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第一等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；

第二计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第二等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；第二计算模块中的常量是第一计算模块中的变量，第二计算模块中常量的数值是与第一计算模块中计算出的第一等效应力的最大值相对应的；

第三计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第三等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤3中的常量与步骤1中的常量是相同的，第三计算模块中常量的数值是与第二计算模块中计算出的第二等效应力的最大值相对应的；

第一生成模块，若步骤1中最大的第一等效应力所对应的变量的角度与步骤3中最大的第三等效应力所对应的变量的角度相同，则用于根据第三等效应力的最大值生成第一参考结果。

本发明实施例提供的半潜式钻井平台的壳单元最大等效应力获取方法，采用反射迭代的方式，与现有技术中的采用全域搜索的方式来找到壳单元的等效应力最大值，导致搜索时间过长，使传统方法不具有实用价值相比，其在每个步骤执行的时候，均将摇摆力和波浪力中的一个设置为常量，另一个设置为变量，并将上一步骤中计算出的等效应力最大值所对应的变量的角度输入到下一个步骤中作为常量，从而通过此种波浪力和摇摆力相互反射迭代式的调整(实际上相互调整的是波浪力所对应的相位角和摇摆力所对应的摇摆方向角)，最终能够在步骤3中得到第一参考结果。此种计算方式相对于传统全域搜索的方法，降低了计算次数，并且保证了一定的计算精度。

进一步，本发明实施例提供的半潜式钻井平台的壳单元最大等效应力获取方法中，还提供了采用双方向迭代计算，并最终通过比较的方式来输出最终结果的方案(第一种可能的实施方式)，双方向迭代计算的方式与前述单方向迭代计算的方式相比，由于这两个计算方向的起始条件不同(指步骤1中的常量和步骤6中的常量是不同的)，进而后续步骤中的执行条件也依次适应变化，最终通过对两个方向的结果进行比较来确定最终的结果，此种方式虽然计算次数相较于单方向迭代方式增加了，但精度得到了提高。

更进一步，本发明实施例提供的半潜式钻井平台的壳单元最大等效应力获取方法中，还提供了步骤3和步骤6中的变量搜索范围在A-60°～A+60°；其中，A为前一步骤中得到的最大的等效应力所对应的变量的角度。经过发明人的反复计算和统计，确定将变量搜索范围设置在这120°的范围内，既能够保证计算精度，也能够降低计算次数，提高了本申请所提供方法的整体效率。

为使本发明的上述目的、特征和优点能更明显易懂，下文特举较佳实施例，并配合所附附图，作详细说明如下。

附图说明

为了更清楚地说明本发明实施例的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。

图1示出了相关技术中所提供的一种传统的计算壳单元最大等效应力的方法流程图；

图2示出了本发明实施例所提供的针对半潜式钻井平台的壳单元提供的最大等效应力获取方法的基本方法流程图；

图3示出了本发明实施例所提供的针对半潜式钻井平台的壳单元提供的最大等效应力获取方法的实例1所对应的流程图。

具体实施方式

下面将结合本发明实施例中附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。通常在此处附图中描述和示出的本发明实施例的组件可以以各种不同的配置来布置和设计。因此，以下对在附图中提供的本发明的实施例的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施例。基于本发明的实施例，本领域技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。

在计算每个壳单元的最大等效应力时，波浪力和摇摆力是相对独立的，并且，考虑到静态荷载的数值相对稳定。因此，传统的计算方法中，通常采用如图1中所示的双层循环方式来计算在不同波浪相位角和不同摇摆方向角的情况下，所对应的等效应力。

具体而言，在图1所示的外层循环中，考虑波浪力，即将0°，2°，4°…358°的相位角对应的波浪力(由波浪而引起的应力分量，包括σ_{w_x},σ_{w_y}及τ_w，其中，σ_{w_x}为波浪力在x方向的应力分量；σ_{w_y}是为波浪力在y方向的应力分量；τ_w为波浪力在壳单元边缘的剪力方向的应力分量)分别叠加到静荷载引起的应力分量(σ_{s_x},σ_{s_y}及τ_s，其中，σ_{s_x}为静荷载在x方向的应力分量；σ_{s_y}是为静荷载在y方向的应力分量；τ_s为静荷载在壳单元边缘的剪力方向的应力分量)之上；内层循环则考虑摇摆力(由半潜平台摇摆运动而产生的应力分量，包括σ_{p_x},σ_{p_y}及τ_p，其中，σ_{p_x}为摇摆力在x方向的应力分量；σ_{p_y}是为摇摆力在y方向的应力分量；τ_p为摇摆力在壳单元边缘的剪力方向的应力分量),即对每一个正在考虑的波浪相位角，将0°，2°，4°…358°的摇摆方向对应的摇摆力(σ_{p_x},σ_{p_y}及τ_p)分别叠加到静荷载及波浪力的组合应力分量(σ_{s_x}+σ_{w_x},σ_{s_y}+σ_{w_y}及τ_s+τ_w)之上，并在组合的应力分量(σ_{s_x}+σ_{w_x}+σ_{p_x}，σ_{s_y}+σ_{w_y}+σ_{p_y},及τ_s+τ_w+τ_p)基础之上，按照如下公式计算对应的等效应力：

其中，σ_x＝σ_{s_x}+σ_{w_x}+σ_{p_x}；σ_y＝σ_{s_y}+σ_{w_y}+σ_{p_y}；τ＝τ_s+τ_w+τ_p。上述计算过程中，使用到了不同应力(波浪力、摇摆力和静态荷载)在不同方向(x方向和y方向)上的分量值，这些分量值的具体数值是半潜式钻井平台的各个有限元单元在平台实际的工作环境/运动中将会经历到的应力分布，由一套复杂的有限元分析流程得到，这套得到分量值的方法已经在相关技术中出现，本申请中不再做详细描述。

简而言之，图1所示的计算等效应力的方法是一种全域搜索法，该方法将每一种可行的波浪相位角所对应的波浪力与每一种可行的摇摆方向所对应的摇摆力进行组合，并再与静态荷载进行组合，来计算出在指定波浪相位角和指定摇摆方向的情况下，所对应的等效应力。如图1所示的方法中，波浪相位角和摇摆方向角所对应的步长为2°，也就是波浪相位角的取值为0°，2°，4°…358°(共180个数值)，类似的，摇摆方向角的取值也为0°，2°，4°…358°(共180个数值)。那么，执行计算的时候，第一轮循环首先确定相位角为0°，摇摆方向角按照0°，2°，4°…358°变化180次，也就得到了180个结果；第二轮循环确定相位角为2°，摇摆方向角依旧按照0°，2°，4°…358°变化180次，也会得到了180个结果…直至最后一轮循环(第180轮)确定相位角为358°，摇摆方向角依旧按照0°，2°，4°…358°变化180次，仍然会得到了180个结果。即计算出的等效应力也就是有180×180＝32400个(计算的总次数也是32400次)。即，波浪相位角为0°、摇摆方向角为0°时的等效应力；波浪相位角为0°、摇摆方向角为2°时的等效应力；波浪相位角为0°、摇摆方向角为4°时的等效应力…波浪相位角为358°、摇摆方向角为358°时的等效应力。之后，从计算出的这32400个结果中，查找数值最大的结果作为最终输出的最大等效应力即可。

按照上述方法，如果将波浪相位角和摇摆方向角所对应的步长由2°调整为1°的话，那计算总次数就会变为360*360＝129600次，如果为了提高所搜的全面性，步长进一步降低(如调整为0.5°甚至更低)，则计算的总次数就会进一步大幅增加。

并且，上述图1所示的方法仅仅是针对一个壳单元进行的计算(以步长为2°为例)，对于一个含有40万个壳单元的半潜平台的整体模型而言，单单是操作工况，一般考虑8个方向共32个设计波，那么共计迭代次数将高达4.15×10¹¹次，采用一台4核3.4GHz主频的微机，大约需要240小时！也就是说，对一个如此寻常规模的半潜平台，如果用传统的双层循环迭代的方式来实现计算每个壳单元的最大等效应力的目的，基本不具备可行性。

针对上述传统方案的不足，本申请提供了半潜式钻井平台的壳单元最大等效应力获取方法，如图2所示，首先对该方法的第一个计算过程进行介绍，该过程包括如下步骤：

步骤1，根据摇摆力、波浪力和静态荷载迭代计算第一等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；

步骤2，根据摇摆力、波浪力和静态荷载迭代计算第二等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤2中的常量是步骤1中的变量，步骤2中常量的数值是与步骤1中计算出的第一等效应力的最大值相对应的；

步骤3，根据摇摆力、波浪力和静态荷载迭代计算第三等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤3中的常量与步骤1中的常量是相同的，步骤3中常量的数值是与步骤2中计算出的第二等效应力的最大值相对应的；

步骤41，若步骤1中最大的第一等效应力所对应的变量的角度与步骤3中最大的第三等效应力所对应的变量的角度相同，则根据第三等效应力的最大值生成第一参考结果。

上述步骤1的执行过程中，可以设置摇摆力为常量，也可以设置波浪力为常量，由于静态荷载通常是以常量的方式出现(不会随角度的变化而变化)因此，后续不再针对性对静态荷载进行说明。步骤1中的常量理论上可以设置为任何数值，但考虑到为了简化计算，可以直接将该常量设置为0(不考虑该常量的角度)。

具体的，步骤1可以设置摇摆力为常量，也可以何止波浪力为常量，这两种设置方式的原理是相同的，下面仅以摇摆力为常量、波浪力为变量的情况进行说明：

如果摇摆力为常量(常量是指在当前步骤执行计算的过程中，数值不会发生变化的量)，那么波浪力就为变量(变量是指在当前步骤执行计算的过程中，每次计算数值都会按照相位角的改变而使数值发生变化的量)，如可相位角取0°，2°，4°…358°(共180个数值)180个数值，那么相对应的，波浪力就有180个取值，步骤1也就会计算180次，进而得到180个计算结果，即得到180个第一等效应力。

步骤2中的常量与步骤1中的常量是不同的，如步骤1中的常量为波浪力，那么步骤2中的常量就为摇摆力；如果步骤1中的常量为摇摆力，那么步骤2中的常量就为波浪力。

步骤2中常量的数值是与步骤1中计算出最大的第一等效应力相对应的，指的是步骤2中常量(波浪力)的数值是由于最大的第一等效应力所决定的。

具体的，步骤2中常量的数值可以是通过如下方式确定的：步骤1完成全部迭代计算后，能够得到大量的第一等效应力(如步长为2°，且在360°的范围内变化，那么第一等效应力的数量就是180个)，之后从这些第一等效应力中选择出数值最大的。如前文中的描述，第一等效应力是由三个参数组成，分别是摇摆力、波浪力和静态荷载。如果步骤1中摇摆力为常量、波浪力为变量，那么数值最大的第一等效应力就对应着一个特定的相位角(计算出最大的第一等效应力的波浪力所对应的相位角)。进而，步骤2中执行计算时所使用的波浪力的数值也就是计算出最大的第一等效应力的波浪力的数值。即，在步骤1中可以增加如下步骤，来确定步骤2中常量的数值：查找多个第一等效应力中最大的第一等效应力；将最大的第一等效应力所对应的变量的数值作为步骤2中常量的数值。本申请中其他步骤中所使用的常量的数值的确定方式均是如此，常量的数值均是前一步骤计算出的最大的等效应力所对应的变量(摇摆力或波浪力)的数值，后文中便不再介绍各个步骤中常量的数值的确定过程。

相类似的，步骤3中的常量也是按照相同的方式，根据步骤2中计算出最大的第二等效应力所对应的变量的数值确定的。具体确定的过程为：查找多个第二等效应力中最大的第二等效应力；将最大的第二等效应力所对应的变量的数值为步骤3中常量的数值。

步骤1-3执行结束后，需要判断步骤1中得到的最大第一等效应力所对应的波浪力的相位角与步骤3中得到的最大第三等效应力所对应的波浪力的相位角是否相同，如果相同，则说明经过步骤3的计算，波浪力的相位角没有发生变化，此时，步骤3所计算出的最大的第三等效应力就可以作为结果输出了。其中，根据第三等效应力的最大值生成第一参考结果，第一参考结果中除了包含第三等效应力的最大值，还可以包含如下参数：该最大值所对应的相位角的角度，和该最大值所对应的摇摆方向角的角度。

实际计算中，经过步骤1-3及步骤41，能够得到较为准确的最大等效应力，当步骤1中最大的第一等效应力所对应的变量的角度与步骤3中最大的第三等效应力所对应的变量的角度不相同时，也可以直接输出第三等效应力作为结果，但此时输出的结果的准确度可能不够，因此，申请人认为，在该种情况下，应当继续进行迭代计算，即执行步骤42，根据摇摆力、波浪力和静态荷载迭代计算第四等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤4中的常量与步骤2中的常量是相同的，步骤4中常量的数值是与步骤3中计算出的第三等效应力的最大值相对应的。

类似的原因，步骤42计算出的结果也并不必然是最准确的，因此还可以增加后续的判断和计算过程。如当步骤2中最大的第二等效应力所对应的变量的角度与步骤4中最大的第四等效应力所对应的变量的角度不相同时，则执行步骤5，根据摇摆力、波浪力和静态荷载迭代计算第五等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤5中的常量与步骤1中的常量是相同的，步骤5中常量的数值是与步骤4中计算出的第四等效应力的最大值相对应的；并根据第五等效应力的最大值生成第一参考结果。

进一步，在某些及特殊的情况下，步骤5所生成的结果(最大的第五等效应力)可能仍然不是等效应力中的最大值，此时还可以通过迭代计算的方式进行进一步计算。即根据第五等效应力的最大值生成第一参考结果包括：

依次迭代执行如下两个步骤，直至符合以下2个条件中的一个时，根据当前步骤得到的等效应力的最大值生成第一参考结果；条件1，步骤11或步骤12的执行次数达到预设阈值；条件2，当前步骤得到的最大的等效应力所对应的变量的角度与前两步骤得到的最大的等效应力所对应的变量的角度相同；

步骤11，根据摇摆力、波浪力和静态荷载迭代计算等效应力，其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤11中的常量与步骤1中的常量是相同的；

步骤12，根据摇摆力、波浪力和静态荷载迭代计算第二等效应力，其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤12中的常量与步骤2中的常量是相同的；步骤11和步骤12中的常量的数值均是与前一步骤中计算出的等效应力的最大值相对应的。

以上介绍了本方法的第一个计算过程，为了提高输出结果的准确度，优选的，还可以在上述第一个计算过程的基础上，增加第二个计算过程和判断过程，第二个计算过程的步骤如下：

步骤6，根据摇摆力、波浪力和静态荷载迭代计算第六等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；步骤6中的常量与步骤1中的常量是不同的；

步骤7，根据摇摆力、波浪力和静态荷载迭代计算第七等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤7中的常量与步骤6中的常量是不同的，步骤7中常量的数值是与步骤6中计算出的第六等效应力的最大值相对应的；

步骤8，根据摇摆力、波浪力和静态荷载迭代计算第八等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤8中的常量与步骤6中的常量是相同的，步骤8中常量的数值是与步骤7中计算出的第七等效应力的最大值相对应的；

若步骤6中最大的第六等效应力所对应的变量的角度与步骤8中最大的第八等效应力所对应的变量的角度相同，则根据第8等效应力的最大值生成第二参考结果；

判断过程如下：

判断第一参考结果是否大于第二参考结果；

若是，则输出第一参考结果；

若否，则输出第二参考结果。

可见，步骤6-8与步骤1-3基本相同，区别在于步骤6中的常量是步骤1中的变量，步骤6中的变量是步骤1中的常量，后续步骤2和7，以及步骤3和8均是如此对调了常量和变量。一般情况下，第一个计算过程与第二个计算过程所得到的结果是相同的，但实际计算中，仍然有10％-15％的概率这两个计算过程得到的结果不同，因此，增加了第二个计算过程和判断的步骤能够进一步提高计算精度。在判断的过程中，如果这第一参考结果和第二参考结果相同(指第一参考结果中的最大等效应力与第二参考结果中的最大等效应力相同)，则输出哪个值作为最终结果都可以，此时，第一参考结果和第二参考结果没有分别。

当然，步骤8并不一定能够得到最优选的结果(当步骤6中最大的第六等效应力所对应的变量的角度与步骤8中最大的第八等效应力所对应的变量的角度不相同时，此时的第8等效应力就不一定是最优结果)，此时还可以增加后续的计算步骤来提高精度，增加的步骤与第一个计算过程类似，此处不过多说明。

下面，分别以一个具体的实施例来说明本申请所提供的方法。

实例1，如图3中所示，分为三个计算过程，第一个计算过程与第二个计算过程可以同时进行，也可以分别进行，第三个计算过程需要等待前两个计算过程均执行结束后才可以执行：

第一个计算过程，由如下步骤101-105组成；

步骤101，将摇摆力引起的应力设置为常量(步骤101中，摇摆力的数值可以设置为0，或其他常量)，将静态荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)与波浪力(包括σ_{w_x},σ_{w_y}，τ_w)以2°的波浪相位角为步长(即波浪相位角分别取2°、4°、6°…358°共180个数值)进行迭代组合，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第一最大等效应力，以及找出第一最大等效应力所对应的波浪相位角α^I；步骤101的计算次数共180次；

步骤102，将波浪力设为常量(步骤102中的波浪力是相位角为α^I时的波浪力，包括σ_{w_x}(α^I),σ_{w_y}(α^I)，τ_w(α^I))，将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、波浪力[σ_{w_x}(α^I),σ_{w_y}(α^I)，τ_w(α^I)]与摇摆力(σ_{p_x},σ_{p_y}，τ_p)以2°的摇摆方向角为步长进行迭代组合，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第二最大等效应力，以及找出第二最大等效应力所对应的摇摆方向角θ^II；步骤102的计算次数共180次；

步骤103，将摇摆力设置为常量，(步骤102中的摇摆力是摇摆方向角为θ^II时的摇摆力，包括σ_{p_x}(θ^II),σ_{p_y}(θ^II)，τ_p(θ^II))；将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、摇摆力[σ_{p_x}(θ^II),σ_{p_y}(θ^II)，τ_p(θ^II)]与波浪力(σ_{w_x},σ_{w_y}，τ_w)以2°的相位角为步长进行迭代组合(搜索区间为α^I-60°～α^I+60°)，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第三最大等效应力σ^III_{eqv_max}，以及找出第三最大等效应力所对应的相位角α^III，步骤103迭代次数是61次；

步骤104，首先判断步骤103中得到的相位角α^III与步骤101中得到的结果α^I是否相同；

步骤1041，如相同，则将第一个计算过程的结果记录为α^w及θ^w(上标w表示该计算结果由以波浪相位角为迭代始所得，其中，α^w＝α^III，θ^w＝θ^II)，并结束第一个计算过程。

步骤1042，如不相同，则将波浪力设为常量(步骤104中的波浪力是相位角为α^III时的波浪力，包括σ_{w_x}(α^III),σ_{w_y}(α^III)，τ_w(α^III))，将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、波浪力[σ_{w_x}(α^III),σ_{w_y}(α^III)，τ_w(α^III)]与摇摆力(σ_{p_x},σ_{p_y}，τ_p)以2°的摇摆方向角为步长进行组合(搜索区间是θ^II-60°～θ^II+60°)，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第四最大等效应力σ^IV_{eqv_max}，以及找出第四最大等效应力所对应的摇摆方向θ^IV，本步骤迭代次数是61；

步骤105，首先判断步骤104中得到的相位角θ^IV与步骤102中得到的结果θ^II是否相同；

步骤1051，如相同，则将第一个计算过程的结果记录为α^w及θ^w(其中，α^w＝α^III，θ^w＝θ^IV)，并结束第一个计算过程。

步骤1052，如不相同，则将摇摆力设置为常量，(步骤105中的摇摆力是摇摆方向角为θ^IV时的摇摆力，包括σ_{p_x}(θ^IV),σ_{p_y}(θ^IV)，τ_p(θ^IV))；将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、摇摆力[σ_{p_x}(θ^IV),σ_{p_y}(θ^IV)，τ_p(θ^IV)]与波浪力(σ_{w_x},σ_{w_y}，τ_w)以2°的相位角为步长进行迭代组合(搜索区间为α^III-60°～α^III+60°)，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第五最大等效应力σ^V_{eqv_max}，以及找出第五最大等效应力所对应的相位角α^V，并将第一个计算过程的结果记录为α^w及θ^w(其中，α^w＝α^V，θ^w＝θ^IV)，并结束第一个计算过程。

第二个计算过程，由如下步骤106-110组成；

步骤106，将波浪力设置为常量(步骤101中，波浪力可以设置为0，或其他常量)，将静态荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)与摇摆力(包括σ_{p_x},σ_{p_y}，τ_p)以2°的摇摆方向角为步长(即摇摆方向角分别取2°、4°、6°…358°共180个数值)进行迭代组合，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第六最大等效应力，以及找出第六最大等效应力所对应的摇摆方向角θ^VI；步骤106的计算次数共180次；

步骤107，将摇摆力设为常量(步骤102中的摇摆力是摇摆方向角为θ^VI时的摇摆力，包括σ_{p_x}(θ^VI),σ_{p_y}(θ^VI)，τ_p(θ^VI))，将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、摇摆力[σ_{p_x}(θ^VI),σ_{p_y}(θ^VI)，τ_p(θ^VI)]与波浪力(σ_{p_x},σ_{p_y}，τ_p)以2°的相位角为步长进行迭代组合，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第七最大等效应力，以及找出第七最大等效应力所对应的相位角α^VII；步骤107的计算次数共180次；

步骤108，将波浪力设置为常量，(步骤102中的波浪力是相位角为α^VII时的波浪力，包括σ_{w_x}(α^VII),σ_{w_y}(α^VII)，τ_w(α^VII))；将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、波浪力[σ_{w_x}(α^VII),σ_{w_y}(α^VII)，τ_w(α^VII)]与摇摆力(σ_{p_x},σ_{p_y}，τ_p)以2°的摇摆方向角为步长进行迭代组合(搜索区间为θ^VI-60°～θ^VI+60°)，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第八最大等效应力σ^VIII_{eqv_max}，以及找出第八最大等效应力所对应的摇摆方向角θ^VIII，步骤108迭代次数是61次；

步骤109，首先判断步骤108中得到的结果θ^VIII与步骤106中得到的结果θ^VI是否相同；

步骤1091，如相同，则将第二个计算过程的结果记录为α^p及θ^p(上标p表示该计算结果由以摇摆方向角为迭代始所得，其中，α^p＝α^VII，θ^p＝θ^VIII)，并结束第二个计算过程。

步骤1092，如不相同，则将摇摆力设为常量(步骤109中的摇摆力是摇摆方向角为θ^VIII时的摇摆力，包括σ_{p_x}(θ^VIII),σ_{p_y}(θ^VIII)，τ_p(θ^VIII))，将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、摇摆力[σ_{p_x}(θ^VIII),σ_{p_y}(θ^VIII)，τ_p(θ^VIII)]与波浪力([σ_{w_x},σ_{w_y}及τ_w)以2°的相位角为步长进行组合(搜索区间是α^VII-60°～α^VII+60°)，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第九最大等效应力σ^IX_{eqv_max}，以及找出第九最大等效应力所对应的相位角α^IX，本步骤迭代次数是61；

步骤110，首先判断步骤109中得到的相位角α^IX与步骤107中得到的结果α^VII是否相同；

1101，如相同，则将第二个计算过程的结果记录为α^p及θ^p(其中，α^p＝α^IX，θ^p＝θ^VIII)，并结束第二个计算过程。

1102，如不相同，则将波浪力设置为常量，(步骤110中的波浪力是相位角为α^IX时的波浪力，包括σ_{w_x}(α^IX),σ_{w_y}(α^IX)，τ_w(α^IX))；将静荷载引起的应力(σ_{s_x},σ_{s_y}，τ_s)、波浪力[σ_{w_x}(α^IX),σ_{w_y}(α^IX)，τ_w(α^IX)]与摇摆力(σ_{p_x},σ_{p_y}，τ_p)以2°的摇摆方向角为步长进行迭代组合(搜索区间为θ^VIII-60°～θ^VIII+60°)，以计算出每个组合所对应的等效应力，并找出其中的最大值，即第十最大等效应力σ^X_{eqv_max}，以及找出第十最大等效应力所对应的摇摆方向角θ^X，并将第二个计算过程的结果记录为α^w及θ^w(其中，α^p＝α^IX，θ^p＝θ^X)，并结束第二个计算过程。

第三个计算过程由如下步骤111组成；

步骤111，比较第一个计算过程的结果中的最大等效应力与第二个计算过程的结果中的最大等效应力，并将数值较大的最大等效应力所对应的结果作为最终结果输出。其中，输出的时候，可以选择将结果中的三个参数(包括最大等效应力、最大等效应力所对应的摇摆方向角和相位角)中的任意一个参数、任意两个参数，或全部参数进行输出。

更具体的，如下表1所示。

表1

表1中，第一行表示的是相位角不同的取值，第一列表示的是摇摆方向角不同的取值。可以看到，相位角和摇摆方向角都是在0-360°的范围内变化的。任意一个相位角和摇摆方向角都对应着一个等效应力。传统的计算方法是将每一个相位角的取值(对应一个波浪力)和一个摇摆方向角的取值(对应一个摇摆力)进行组合来计算等效应力，也就是传统的方法是将表1中所有的等效应力均计算出来。

简单来看传统的计算方法，其采用的是全域迭代(扫描)计算的方式，即将相位角的每一种取值和摇摆方向角的每一种取值进行组合，如果相位角的取值有180种选择，摇摆方向角也有180种选择的话(通常会将360°按照步长为2°进行取值，也就是取值为0°、2°、4°…358°)，那么可能的取值也就是180*180＝32400次，之后，再从这32400个结果中选择一个最大的结果输出。

整体来看实例1中所提供的方案，其核心在于根据等效应力分布的特点，采用局域迭代计算的方式来查找等效应力中的最大值。即每轮计算的时候，均将一个参数(相位角或摇摆方向角中的一个)设置为常量，按照预设的步长(如2°)来改变另一个参数(相位角或摇摆方向角中的另一个)，进而确定出当前步骤中的最大等效应力，再将该最大等效应力所对应的变量参数的取值输入到下一个步骤中，由下一个步骤对计算结果进一步优化。下一个步骤中的计算结果(最大等效应力的数值)如果和当前步骤一致，则输出结果，如果下一个步骤中的计算结果的数值比当前结果大，则继续计算，直至计算到当前计算过程的最后一步，再输出整个计算过程的结果。而后，在得到了两个计算过程的结果后，便可以将这两个结果中，最大等效应力数值较大的结果输出。

并且，在上述实例1中，步骤103-105，以及步骤108-110中搜索区间不再是360°，而是缩小为120°(如步骤103中的搜索区间为α^I-60°～α^I+60°；步骤108中的搜索区间为θ^VI-60°～θ^VI+60°)。120°这个搜索区间是经过实测后得到的结果，这个搜索区间的范围增大对最终结果的准确程度一般不会提高，但同时会增加整体的计算量。

实际使用中，如果以步长为2°来计算，使用实例1中所示的方案，其计算的总次数最少为842次(步骤14直接输入第一个计算过程的结果，以及步骤19直接输出第二个计算过程的结果的情况下)，至多为1086次(步骤15经过判断和计算后才输出第一个计算过程的结果，以及步骤20经过判断和计算后才输出第一个计算过程的结果)，这与传统技术中的全域扫描方法所需要的32400次相比，计算次数大大下降，实例1中所提供方案的计算次数为传统方法的计算次数的1/30，因而实例1中所提供方案的效率提高了30倍。

并且，通过实际计算和分析，实例1中所提供的方法与传统的全域搜索方法相比，这两种方法计算出的等效应力最大值在96％的概率上完全一致，等效应力最大值的数值出现0.5％以上误差的概率小于0.1％，最大误差小于3％。可见实例1中所提供的方法能够在降低计算从次数的情况下，保证计算精度稳定性较强。

下面有两点需要说明。

第一点，本申请实例1中所提供的方案中，第一个计算过程与第二个计算过程十分相似，二者的主要区别在于首个步骤中，设置为常量的参数不同，即第一个计算过程的首个步骤，步骤11中摇摆力为常量；而第二个计算过程的首个步骤，步骤16中，波浪力为常量。

实际操作中，第一个计算过程得到的结果与第二个过程得到的结果有很大概率是相同的，经过实际测算，这两个结果有85％左右的概率是相同的。

相对于传统计算最大等效应力的方法，只使用第一个计算过程或者只使用第二个计算过程也可以达到降低计算总次数的要求，但相对于实例1的整体方案而言，只使用第一个计算过程，或只使用第二个计算过程的计算精度(主要找到等效应力最大值的概率)会有一定的下降。因此，在实际操作的时候，如果对时间要求较高，对精度要求较低，可以第一个计算过程或第二个计算过程单独使用的方式，来找到等效应力的最大值；如果对时间要求较低，对精度要求较高，则应当采用实例1的整体方案作为解决方案，来找到等效应力的最大值。

第二点，实际使用的时候，本领域技术人员可能会发现传统的全局搜索方法的计算次数过多(为实例1中所提供的方法的计算次数的30倍左右)、计算时间过长，这直接导致了传统的计算方法不适用于真实环境。因此本领域技术人员通常会想到在各个具体的计算步骤中采用放大步长(如计算步长由2°改变为4°、6°甚至更大的数值)的方法来降低计算次数，进而降低计算的整体时间。但使用此种方式来降低计算次数会大幅度降低最终结果的精度(计算出的最大等效应力是实际的最大等效应力的概率)。

本申请提供了相应的保证计算精度和计算时间的方法(即实例1中所公开的方法)主要是针对每个步骤中迭代计算时步长较小的情况所设计的(如迭代的步长为3°或更小，此时每个步骤的计算次数大于120次)，主要原因是，步长较大的时候，传统方法的迭代次数比较少，使用实例1中的方法，整体计算次数下降的不是很明显。

下面以一个带有数据的计算过程来说明使用实例1中方法的中间结果和最终结果。

在某特定条件下，静荷载应力分量：σ_s＝(-46.5，8.5，75.7)；

波浪力分量实部σ^R_w＝(1.8，-0.6，1.7)；虚部σ^I_w＝(2.4，2.8，1.5)；

摇摆力中，纵摇应力分量σ_Pitch＝(33.2，32.6，17.1)；横摆应力分量σ_Roll＝(48.9，41.3，6.6)。

使用传统的全域搜索法最大等效应力175.236，对应波浪相位角52度，对应摇摆方向角28度。

使用实例1中的反射式迭代法：

步骤101完成后：最大等效应力143.769，对应相位角48度，迭代次数180；

步骤102完成后：最大等效应力175.227，对应相位角48度，摇摆方向角28度，迭代次数达到360；

步骤103完成后：最大等效应力175.236，对应相位角52度，摇摆方向角28度，迭代次数达到421；

步骤104完成后：最大等效应力175.236，对应相位角52度，摇摆方向角28度，迭代次数达到482；

因步骤104得到的摇摆方向θ₁与步骤102得到的结果θ相同，步骤105跳过；

步骤106完成后：最大等效应力171.371，对应摇摆方向26度，迭代次数达到662；

步骤107完成后：最大等效应力175.225，对应相位角52度，摇摆方向角26度，迭代次数达到842；

步骤108完成后：最大等效应力175.236，对应相位角52度，摇摆方向角28度，迭代次数达到903；

步骤109完成后：最大等效应力175.236，对应相位角52度，摇摆方向角28度，迭代次数达到964；

因步骤109得到的相位角α₁与步骤107得到的结果α相同，步骤110跳过；

反射是迭代最终结果：最大等效应力175.236，对应波浪相位角52度，对应摇摆方向角28度，与传统迭代结果完全一致，但迭代次数只有964次。

以上提供了本申请所提供的半潜式钻井平台的壳单元最大等效应力获取方法的整体过程，下面还提供了与该方法相对应的半潜式钻井平台的壳单元最大等效应力获取装置，该装置包括如下模块：

第一计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第一等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；

第二计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第二等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；第二计算模块中的常量是第一计算模块中的变量，第二计算模块中常量的数值是与第一计算模块中计算出的第一等效应力的最大值相对应的；

第三计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第三等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；步骤3中的常量与步骤1中的常量是相同的，第三计算模块中常量的数值是与第二计算模块中计算出的第二等效应力的最大值相对应的；

第一生成模块，若步骤1中最大的第一等效应力所对应的变量的角度与步骤3中最大的第三等效应力所对应的变量的角度相同，则用于根据第三等效应力的最大值生成第一参考结果。

第六计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第六等效应力；其中，摇摆力和波浪力中的一个为预设的常量，另一个为变量；第六计算模块中的常量与第一计算模块中的常量是不同的；

第七计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第七等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；第七计算模块中的常量与第六计算模块中的常量是不同的，第七计算模块中常量的数值是与第六计算模块中计算出的第六等效应力的最大值相对应的；

第八计算模块，用于根据摇摆力、波浪力和静态荷载迭代计算第八等效应力；其中，摇摆力和波浪力中的一个为常量，另一个为变量；第八计算模块中的常量与第六计算模块中的常量是相同的，第八计算模块中常量的数值是与第七计算模块中计算出的第七等效应力的最大值相对应的；

若第六计算模块中最大的第六等效应力所对应的变量的角度与第八计算模块中最大的第八等效应力所对应的变量的角度相同，则根据第8等效应力的最大值生成第二参考结果；

判断模块，用于判断第一参考结果是否大于第二参考结果；

若是，则输出第一参考结果；

若否，则输出第二参考结果。

优选的，其中第三计算模块或第八计算模块中，变量的搜索范围是A-60°～A+60°；其中，A为前一模块中得到的最大的等效应力所对应的变量的角度。

所属领域的技术人员可以清楚地了解到，为描述的方便和简洁，上述描述的系统、装置和单元的具体工作过程，可以参考前述方法实施例中的对应过程，在此不再赘述。

在本申请所提供的几个实施例中，应该理解到，所揭露的方法，可以通过其它的方式实现。以上所描述的装置实施例仅仅是示意性的，例如，所述模块的划分，仅仅为一种逻辑功能划分，实际实现时可以有另外的划分方式，又例如，多个模块或组件可以结合或者可以集成到另一个系统，或一些特征可以忽略，或不执行。另一点，所显示或讨论的相互之间的耦合或直接耦合或通信连接可以是通过一些通信接口，装置或单元的间接耦合或通信连接，可以是电性，机械或其它的形式。

所述功能如果以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：U盘、移动硬盘、只读存储器(ROM，Read-Only Memory)、随机存取存储器(RAM，Random Access Memory)、磁碟或者光盘等各种可以存储程序代码的介质。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应所述以权利要求的保护范围为准。