基于混合扩展方式的云端虚拟机的优化配置方法及其系统与流程

本发明涉及的是一种云端虚拟机配置领域的技术，具体是一种基于混合扩展方式的云端虚拟机的优化配置方法及其系统。

背景技术：

得益于云计算的按需付费定价模型，越来越多的企业和开发者愿意将他们的服务和应用程序从本地的基础设施上迁移到云端去。然而，由于这些服务或应用的工作负载会产生很大的波动，想要做一个成本有效的虚拟机配置是及其困难的。即使是很有经验的云端管理员都由于无法准确预测将来一段时间内的工作负载，而无法做出有效的虚拟机配置。目前针对虚拟机配置的简单方式就是用横向扩展的方式，即只使用一种虚拟机，并通过调节虚拟机的数目来达到成本有效。但由于云端虚拟机的价格模型通常都不是线性的，横向扩展方式并不能为用户带来最大的成本效率。

李雅普诺夫优化技术通常被用来求解时均意义上的优化量。在优化问题中，有一大类问题是与时间相关的，例如与工作负载相关的问题就是随着时间变化而不断变化的。因此时均意义上的优化可以更好地优化全局系统的状态。而带有时均变量的优化问题很难用通常的凸优化方法进行解决，李雅普诺夫优化技术就可以被用来解决这类问题。李雅普诺夫优化技术原本来源于自动控制领域中的李雅普诺夫稳定性。因此最初该技术也是用于进行动态队列网络中的最优控制。但由于该技术的优秀性质，之后被拓展到其他领域用于解决求解时均量的优化问题。

经过对现有技术的检索发现，中国专利文献号CN103186410A，公布日2013.7.3，公开了一种虚拟机器的配置方法与使用该方法的服务器系统，包括：产生一虚拟丛集，其中该虚拟丛集具有多个虚拟机器；接收一配置指令；依据该配置指令，于多个配置策略中取得其一作为一选择配置策略；以及依据该选择配置策略，将该些虚拟机器分配至对应的节点。但该技术需要根据各性能指标的优先级进行配置，往往不能兼顾；通常服务或应用程序的工作负载动态变化，难以精确预测，因此不同配置策略间的切换需要整体重新配置，增加了切换所需的时间，不利于对用户的需求判断以及对成本的长期优化。

技术实现要素：

本发明针对现有技术存在的上述不足，提出一种基于混合扩展方式的云端虚拟机的优化配置方法及其系统，通过构造以成本优化为目标，迁移开销和服务能力为限制条件的优化模型，利用李雅普诺夫技术转化为不含时均量的优化模型，求解当前时刻最优的多种类型的虚拟机配置，同时保证用户体验和成本效率。

本发明是通过以下技术方案实现的：

本发明涉及一种基于混合扩展方式的云端虚拟机的优化配置方法，首先通过构造无迁移时的优化模型，得到优化后的虚拟机配置；然后对优化前后的虚拟机配置进行偏差计算，判断是否需要迁移；如果不需要即直接应用优化后的虚拟机配置，否则向用户请求其对迁移开销和成本效率的偏好情况，构造李雅普诺夫单时槽优化模型，得到单时槽优化后的虚拟机配置并应用。

所述的无迁移时的优化模型为：其中：T为最大时间槽数，t为时间槽，x为虚拟机配置决策，K为虚拟机类型数，i为虚拟机类型，c为不同类型虚拟机的价格，μ为不同类型的虚拟机所能服务的最大请求数，Γ为时均后用户所能容忍的迁移开销的阈限，α为迁移开销，λ为当前实际到达的请求数目，即实际工作负载。

所述的迁移开销α定义为：其中：D为当前时刻虚拟机的镜像大小，b为网络带宽，s为虚拟机的开机时间。

所述的偏差计算是指：计算相邻两个时间槽的虚拟机配置x_i(t)和x_i(t-1)的差别，如果x_i(t)-x_i(t-1)≥0，或者x_i(t)-x_i(t-1)≤0，则无迁移发生；如果对某些i，x_i(t)-x_i(t-1)≥0，对另外的i，x_i(t)-x_i(t-1)≤0，则有迁移发生。

所述的李雅普诺夫单时槽优化模型为：其中：V为用户对迁移开销和成本效率的偏好情况，即总价格，Q(t)为虚拟队列，B＝s-Γ。

本发明涉及一种基于上述优化配置方法的系统，包括：无迁移虚拟机配置模块、迁移判断模块、迁移虚拟机配置模块以及配置应用模块，其中无迁移虚拟机配置模块与迁移判断模块相连并传输虚拟机配置信息，迁移判断模块与迁移虚拟机配置模块相连并传输迁移情况信息，无迁移虚拟机配置模块、迁移虚拟机配置模块分别与配置应用模块相连并传输配置信息。

技术效果

与现有技术相比，本发明不同于现有的云服务成本效率，即通常是通过制定一种虚拟机类型，通过增加或减少其使用数量来匹配工作负载和基础设施使用效率的平衡，从而取得较高的成本效率；而是引入混合扩展的方式，设置几种类型的虚拟机，并解决随之产生的有效数据迁移的问题，在成本效率和迁移开销之间取得平衡，达到最优的成本效率。

附图说明

图1为优化配置方法流程图；

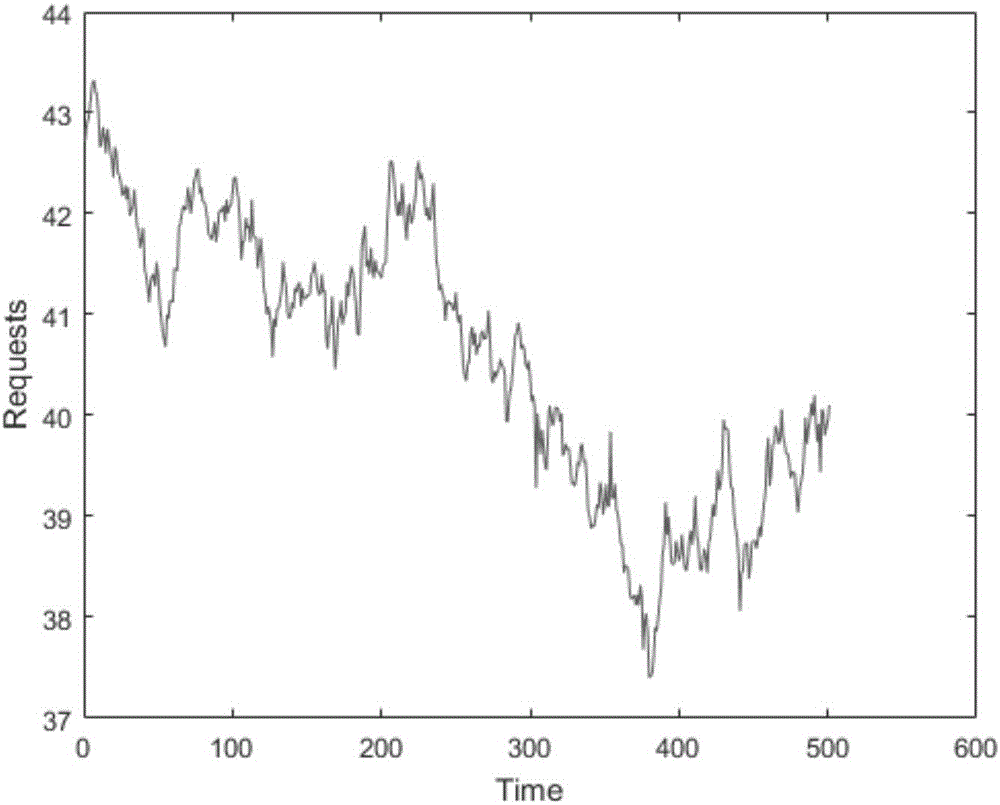
图2为请求到达的数量随时间变化的工作负载示意图；

图3为虚拟机迁移机制；

图中：(a)为直接迁移机制，(b)为冷迁移机制；

图4为优化配置系统示意图。

具体实施方式

下面对本发明的实施例作详细说明，本实施例在以本发明技术方案为前提下进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。

实施例1

如图1所示，本实施例包括以下步骤：

步骤1、通过构造无迁移时的优化模型，得到优化后的虚拟机配置。

如图2所示，由于工作负载的变化情况通常是不稳定的，通过预测将来一段时间内的负载情况来决定当前时刻的虚拟机配置是不现实的。

所述的无迁移时的优化模型为：其中：T为最大时间槽数，t为时间槽，x为虚拟机配置决策，K为虚拟机类型数，i为虚拟机类型，c为不同类型虚拟机的价格，μ为不同类型的虚拟机所能服务的最大请求数，Γ为时均后用户所能容忍的迁移开销的阈限，α为迁移开销，λ为当前实际到达的请求数目，即实际工作负载。

所述的无迁移时的优化模型为一个以成本效率为目标，迁移开销和服务能力为限制条件的最优化问题。

所述的迁移开销α为一个与网络带宽、虚拟机镜像大小和迁移机制相关的量，因此，迁移开销α根据冷迁移机制定义为：其中：D为当前时刻虚拟机的镜像大小，b为网络带宽，s为虚拟机的开机时间。

所述的当前时刻虚拟机的镜像大小D的值可以设为关机的旧虚拟机的镜像总大小。

如图3所示，所述的冷迁移机制与直接从虚拟机迁移到虚拟机的直接迁移机制不同，即虚拟机镜像需先上传至镜像服务器，再下载到新的虚拟机上；因此，迁移的传输时间变为直接迁移的2倍。

因此，无迁移时的优化模型的成本效率、迁移开销都是时均的，且有变量趋于无穷大，因而很难采用传统的解凸优化的方法解决。

步骤2、对优化前后的虚拟机配置进行偏差计算，判断是否需要迁移；如果不需要即直接应用优化后的虚拟机配置，否则进入步骤3。

所述的偏差计算是指：计算相邻两个时间槽的虚拟机配置x_i(t)和x_i(t-1)的差别，如果x_i(t)-x_i(t-1)≥0，或者x_i(t)-x_i(t-1)≤0，则无迁移发生；如果对某些i，x_i(t)-x_i(t-1)≥0，对另外的i，x_i(t)-x_i(t-1)≤0，则有迁移发生。

步骤3、向用户请求其对迁移开销和成本效率的偏好情况，构造李雅普诺夫单时槽优化模型，得到单时槽优化后的虚拟机配置并应用。

所述的构造李雅普诺夫单时槽优化模型具体包括以下步骤：

S1：构造虚拟队列Q描述迁移开销限制条件。

所述的虚拟队列Q的表达式为：Q(t+1)＝max{Q(t)+α(t)-Γ,0}，Q(0)＝0。

S2：构造李雅普诺夫函数及李雅普诺夫偏移。

所述的李雅普诺夫函数为：

所述的李雅普诺夫偏移为：ΔL(Q(t))＝E{L(t+1)-L(t)|Q(t)}，其中：E为期望。

S3：求出李雅普诺夫偏移ΔL(Q(t))的上限。

所述的李雅普诺夫偏移ΔL(Q(t))的上限为：其中：B＝s-Γ。

S4：构造李雅普诺夫单时槽优化模型。

所述的李雅普诺夫单时槽优化模型为：其中：V为用户对迁移开销和成本效率的偏好情况，即总价格。

通过求解李雅普诺夫单时槽优化模型，可解得当前时刻的虚拟机配置，从而取得成本效率和迁移开销之间的平衡。

所述的求解可采用凸优化技术或贪心方法。

如图4所示，本实施例涉及基于上述优化配置方法的系统，包括：无迁移虚拟机配置模块、迁移判断模块、迁移虚拟机配置模块以及配置应用模块，其中无迁移虚拟机配置模块与迁移判断模块相连并传输虚拟机配置信息，迁移判断模块与迁移虚拟机配置模块相连并传输迁移情况信息，无迁移虚拟机配置模块、迁移虚拟机配置模块分别与配置应用模块相连并传输配置信息。

本实施例在横向扩展的基础上，配置多种类型的虚拟机，充分利用不同类型虚拟机的定价优势，引入混合扩展的方式，同时也引入了虚拟机有效数据迁移的问题。在横向扩展的情况下，不会出现有效数据需要传输的情况；在混合扩展的情况下，会出现小虚拟机扩展为大虚拟机的情况，此时就需要将小虚拟机的数据传输给大虚拟机，从而保证服务的连续性和稳定性。正由于此，在引入混合扩展后，还需要权衡迁移时间代价和成本效率之间的关系。本实施例利用李雅普诺夫优化技术，设计了混合扩展在线方法来全局优化用户的使用成本，并且优化了混合扩展过程中产生的迁移开销。

本实施例在指定大小的时槽内运行，随着工作负载的不断变化，可以自适应地做出最优的虚拟机配置选择。