一种临氢厚壁圆柱壳弹性极限载荷预测方法与流程

本发明涉及临氢承载结构的弹性响应预测领域，具体是基于氢脆的HELP理论预测厚壁圆柱壳的弹性极限载荷。
背景技术：
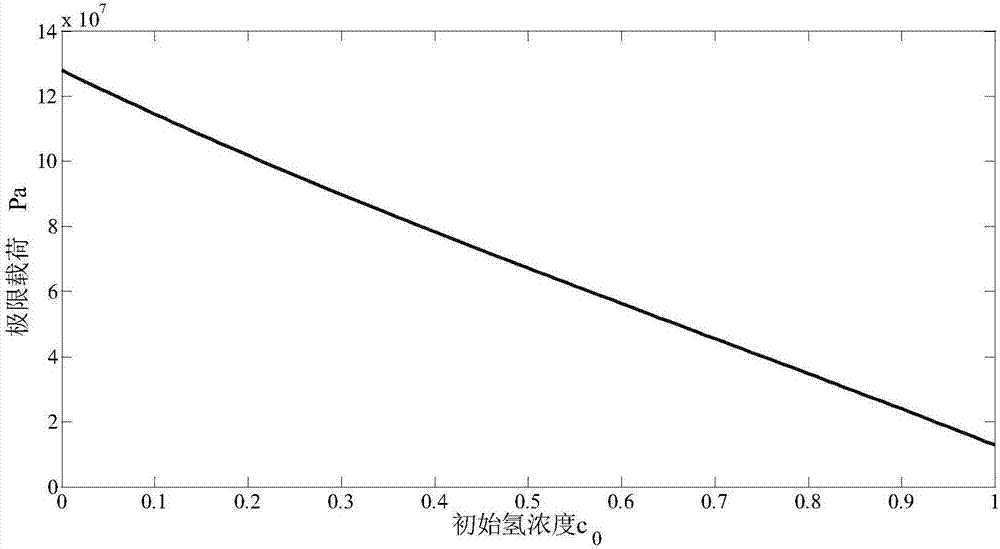
：圆柱壳是氢系统中储氢和输氢过程中的关键承压元件，确定厚壁圆柱壳在氢环境下的弹性极限载荷是设计储氢罐、加氢反应器等临氢设备时必须考虑的问题。现有的预测圆柱壳极限载荷的方法并未将氢环境对圆柱壳的影响考虑在内，同时由于氢损伤本构关系的复杂性，采用传统的增量法来预测圆柱壳在氢环境下的极限载荷及其复杂，难以在工程上推广。因此提出一种简单的预测临氢圆柱壳弹性极限载荷的方法具有工程意义。本发明将氢脆的氢促进塑性局部化理论(HELP)应用于厚壁圆柱壳，提出了一种临氢厚壁圆柱壳预测弹性极限载荷的简化方法。技术实现要素：本发明的目的在于针对现有技术的不足，提供一种简化的临氢厚壁圆柱壳弹性极限载荷预测方法，该方法根据大气环境中与氢环境中圆柱壳的应力响应之间的关系，直接构造临氢圆柱壳弹性极限载荷问题的控制方程。在预测极限载荷时考虑了氢环境对圆柱壳性能的影响。本发明的目的是通过以下技术方案来实现的：一种临氢厚壁圆柱壳弹性极限载荷预测方法，包括以下步骤：步骤1：令厚壁圆柱壳的极限载荷p的初值为p＝0；步骤2：按照以下方程计算周向应力σθ和径向应力σr；σr＝-p其中a为圆柱壳内半径，b为圆柱壳外半径。步骤3：按照以下方程组计算氢浓度c；其中，E为材料的弹性模量，ν为材料的泊松比，VH表示氢在母材中的偏摩尔体积，VM为母材的摩尔体积，α为每单位晶格的氢陷阱数，β每单位晶格的晶格间隙结合位点数，NL＝NA/VM为每单位体积的金属原子数量，NA为阿伏伽德罗常数，NT表示每单位体积的陷阱个数。R为理想气体常数，T为开氏温标，c0为无载荷时圆柱壳内的氢浓度，WB为材料的氢陷阱结合能。步骤4：计算轴向应力σz步骤5：计算函数值g其中σ0为材料的初始屈服强度，ξ为表征氢损伤程度的参数。步骤6：判断g值大小，若|g|≥εerr，则执行步骤7至步骤8，否则结束计算，得到临氢厚壁圆柱壳弹性极限载荷，其中εerr为收敛容差，可取εerr＝10-6；步骤7：按照下式计算极限载荷p1其中步骤8：令p＝p1，返回步骤2。进一步地，所述步骤3采用牛顿法求解氢浓度c，具体包括以下子步骤：步骤301：设置氢浓度初值c＝c0；步骤302：根据当前氢浓度c，按照下式计算各个参数：步骤303：计算以下函数值g：步骤304：判断g值大小，若|g|≥εerr，则执行步骤305至步骤306，否则结束计算，得到氢浓度c，其中εerr为收敛容差，可取εerr＝10-6；步骤305：按照下式计算氢浓度c1其中步骤306：令c＝c1，返回步骤302。本发明具有以下优点：采用求解非线性方程组的方法直接预测临氢厚壁圆柱壳的弹性极限载荷，不需要编写氢损伤材料的本构模型的有限元程序。在预测极限载荷时考虑了氢对材料的损伤作用，本发明预测得到的极限载荷相比于现有方法偏于安全。附图说明图1为本发明的实施对象简图；图2为本发明实例计算得到的弹性极限载荷与初始氢浓度c0的关系。具体实施方式以下以图1和表1所示的实例为实施对象，对本发明作进一步说明。图1所示的实例是一个两端约束的厚壁圆柱壳，其内半径和外半径分别为a和b，在无应力状态下浓度为c0的氢在圆柱壳内均匀分布。本发明可以预测处于氢环境中的圆柱壳的弹性极限载荷。表1实例用到的材料参数和几何参数参数数值内半径a0.5m外半径b0.75m弹性模量E115GPa泊松比υ0.34氢的偏摩尔体积VH1.18×10-6m3/mole金属的摩尔体积VM10.825×10-6m3/mole屈服强度σ0400MPa陷阱密度NT4.2855×1019晶格间隙位点数β1.0氢陷阱数α1.0温度T300K氢损伤因子ξ0.1陷阱结合能WB29.3KJ/mole本发明方法的实现过程如下：步骤1：给定一个初始氢浓度c0，例如c0＝0.1，令厚壁圆柱壳的极限载荷p的初值为p＝0；步骤2：将当前的极限载荷p带入以下方程计算周向应力σθ和径向应力σr；σr＝-p其中圆柱壳内半径a，外半径b按表1中取值；步骤3：按照以下方程组计算氢浓度c；其中各参数按表1中取值，步骤3具体包括以下子步骤：步骤301：设置氢浓度初值c＝c0；步骤302：根据当前氢浓度c带入下式计算各个参数：步骤303：将步骤202得到的参数带入以下函数值，计算函数值g：步骤304：判断g值大小，若|g|≥εerr，则执行步骤205至步骤206，否则结束计算，得到氢浓度c，其中收敛容差取εerr＝10-6；步骤305：按照下式计算氢浓度c1其中所需各参数均由步骤302计算得到；步骤306：令c＝c1，返回步骤302。步骤4：将步骤2得到的周向应力σθ和径向应力σr以及步骤3得到的氢浓度c带入下式计算轴向应力σz：步骤5：将步骤2得到的周向应力σθ和径向应力σr，步骤3得到的氢浓度c以及步骤4得到轴向应力σz带入下式计算函数值g其中材料的初始屈服强度σ0和氢损伤因子ξ按表1取值。步骤6：判断g值大小，若|g|≥εerr，则执行步骤7至步骤8，否则结束计算，得到临氢厚壁圆柱壳弹性极限载荷p，其中收敛容差取εerr＝10-6；步骤7：按照下式计算极限载荷p1其中步骤8：令p＝p1，返回步骤2。采用不同的初始氢浓度c0(0≤c0≤1)重复步骤1至步骤8可以得到临氢圆柱壳弹性极限载荷与初始氢浓度之间的关系，如图2所示。当前第1页1 2 3