高性能随机数发生方法及发生器与流程

本发明涉及一种新型随机数发生器，尤其涉及一种高性能随机数发生方法及发生器。

背景技术：

随机数在蒙特卡罗计算和信息加密等领域起着重要的作用。例如密码算法里的密钥要求是随机数，另外许多密码协议的中间过程也需要随机数，如量子密码的BB84协议等。随机数发生器质量的好坏决定了密码产品自身的安全性。

随机数发生器是指产生随机数的设备或算法。随机数发生器质量的好坏决定了密码产品的安全性的高低。理想的随机数的产生可以看成是投掷硬币的结果，根据硬币正面或反面标记为“0”或“1”，对于每一次投掷结果，“0”或“1”出现的概率均为1/2。并且投掷结果之间相互独立，即前面的投掷结果不会影响到后面的结果。在实际应用中，以这种方式产生的随机数显然是不现实的，但是它可以作为一种度量标准来评估实际的随机数发生器。

现代随机数发生器一般使用物理方法产生真随机数，不再使用算法来产生伪随机数。各种随机物理过程如宇宙噪声、电路的热噪声和放射性衰变均可用来产生随机物理信号,例如早在70年代就出现采用粒子放射源作为随机信号源的真随机数发生器。随着微电子学的发展,廉价的高质量集成电路芯片的出现,使得电路的热噪声成为最易于获得的随机物理信号,因此现代多数真随机数发生器设计采用电路的热噪声作为随机信号源。

尽管用物理方法产生的随机数是真随机数，但是由于数据采集和A/D转换等中间过程的误差，最后得到的二元序列往往不能通过国家密码管理局《随机性检测规范》规定的所有15项检测，必须要对采集到的数据进行处理后才能得到高性能的随机数。现有的处理方法例如使用线性反馈移位寄存器对采集到的数据进行变换，或者使用混沌算法对数据进行变换等方法都不能完全解决生成高性能随机数的问题。

技术实现要素：

本发明所要解决的技术问题是，针对上述现有技术的不足，提供一种高性能随机数发生方法及发生器，本高性能随机数发生方法及发生器对采集到的数据进行处理，得到高性能随机数，能够持续生成完全随机性的随机数，所产生的高性能随机数符合国家密码管理局《随机性检测规范》中所有规定检测。

为解决上述技术问题，本发明采用的技术方案为：高性能随机数发生方法，其特征在于包括以下步骤：

首先，通过物理数据采集模块生成随机性较差的随机数，所述性能较差的随机数为原始随机数；

其次，通过随机性算法处理模块对原始随机数进行随机性算法处理以得到真随机数。

作为本发明进一步改进的技术方案,所述随机性算法处理模块对原始随机数进行有理数逼近无理数的算法变换；所述算法变换首先得到渐近分数，然后对渐近分数使用大整数除法得到结果，再将结果进行二进制展开，最终得到高随机性的随机序列。

作为本发明进一步改进的技术方案,通过伪随机数生成芯片生成随机性较好的伪随机数；通过随机性算法处理模块对原始随机数与随机性很好的伪随机数进行按位异或，最终得到高随机性的真随机数。

作为本发明进一步改进的技术方案,所述随机性算法处理模块对原始随机数与随机性很好的伪随机数进行按位异或后，接着对异或结果按位取反，最终得到高随机性的真随机数。

作为本发明进一步改进的技术方案,所述伪随机数生成模块使用伪随机数算法得到随机性很好的伪随机数；最后使用伪随机数比特位0或1，按位决定物理采集数对应的比特位是否翻转，最终得到高随机性的真随机数。

为实现上述技术目的,本发明提供的另一种高性能随机数发生方法，包括以下步骤：

首先物理采集随机数，将该随机性较差的随机数以每s个bit进行截取；每s个bit代表一个s位的二进制无符号整数，依次作为连分数的部分商x₁,…,x_n,…，置x₀＝0；无限连分数<x₀，...，x_n，...>一定收敛于一个无理数ξ；

因为x₀＝0，所以无理数ξ的小数点左边恒为0，用小数点右边的二进制展开作为随机数；

用循环语句依次计算无理数ξ的每个渐近分数，用条件k_nk_n+1≥2^m作为循环终止的条件；

循环终止后，利用渐近分数可以将无理数ξ以二进制方式展开到小数点后m位；由于小数点右边最多可能连续出现s个0，将无理数ξ以二进制方式展开到小数点后s+m位，再将最左边的s个bit截取掉，剩下m个bit作为随机数。

s、n、m都可以取任意长，s取32或64，m取1万到10万之间；n由m通过计算决定，满足k_nk_n+1≥2^m。

为实现上述技术目的,本发明还提供了一种高性能随机数发生器，包括用于生成随机性能较差的随机数的物理数据采集模块，所述性能较差的随机数为原始随机数；还包括用于对原始随机数进行随机性算法处理以得到真随机数的随机性算法处理模块。

作为本发明进一步改进的技术方案,所述随机性算法处理模块用于对原始随机数进行有理数逼近无理数的算法变换；所述算法变换首先得到渐近分数，然后对渐近分数使用大整数除法得到结果，再结果进行二进制展开，最终得到高随机性的随机序列。

作为本发明进一步改进的技术方案,还包括伪随机数生成芯片，所述伪随机数生成芯片用于生成随机性较好的伪随机数；所述随机性算法处理模块用于对原始随机数与随机性很好的伪随机数进行按位异或，最终得到高随机性的真随机数。

作为本发明进一步改进的技术方案,所述随机性算法处理模块对原始随机数与随机性很好的伪随机数进行按位异或后，接着对异或结果按位取反，最终得到高随机性的真随机数；所述伪随机数生成模块使用伪随机数算法得到随机性很好的伪随机数；最后使用伪随机数比特位0或1，按位决定物理采集数对应的比特位是否翻转，最终得到高随机性的真随机数。

本发明使用连分数方法对无理数进行有理逼近来对物理方法产生的随机数进行处理产生高性能的随机数。以下是本发明的原理及对采集到的数据的处理步骤。本文中直接引用而不证明的结论，请参考华罗庚《数论导引》第十章。

无理数ξ＝<x₀，x₁，...，x_n，...>，其中x_i是整数，i＞0时，x_i＞0。其渐近分数

其中h_n，k_n满足下列递归等式(1)

h_n＝x_nh_n-1+h_n-2

k_n＝x_nk_n-1+k_n-2

对于任何整数n≥-1，定义矩阵

其中规定在这样的规定下，递归等式(1)对于任何整数n≥0都成立。

上述递归等式可以用矩阵表示为：对于任何整数n≥0，

证明：根据矩阵乘法规则，我们得到

根据递归等式(1)，上式右边等于因为将M_n和M_n-1代入等式(3)，得到等式(2)。

可以证明：对于任何整数n≥0，

证明：用归纳法证明。当n＝0时，根据(2)式，式成立。假设n＝k时(4)式成立，那么n＝k+1时，根据(2)式，所以n＝k+1时(4)式也成立。

对(4)式两边取行列式得到，

将行列式展开后得到h_nk_n-1-h_n-1k_n＝(-1)ⁿ⁺¹(5)，所以对于任何整数n≥0，最大公约数gcd(h_n，k_n)＝1，因此每个渐近分数都是既约分数。可以证明无限简单连分数<x₀，x₁，...，x_n，...>(其中x_i是整数，i＞0时，x_i＞0)一定收敛于一个无理数。对于任何整数n≥0，无理数ξ用其渐近分数逼近的误差估计不等式

本发明的是将无理数以二进制方式展开到小数点后指定位数来获取高性能随机数。以下是具体步骤：

根据(6)，只要满足则利用渐近分数可以将无理数ξ以二进制方式展开到小数点后m位。这条件等价于k_nk_n+1≥2^m(7)。在工程实现时，首先将用物理方法产生的随机性较差的随机数以每s个bit进行截取。每s个bit代表一个s位的二进制无符号整数，依次作为连分数的部分商x₁,…,x_n,…，我们置x₀＝0。无限连分数<x₀，...，x_n，...>一定收敛于一个无理数ξ。因为x₀＝0，所以无理数ξ的小数点左边恒为0，我们用小数点右边的二进制展开作为随机数。用循环语句依次计算无理数ξ的每个渐近分数，用条件(7)作为循环终止的条件。循环终止后，利用渐近分数可以将无理数ξ以二进制方式展开到小数点后m位。考虑到小数点右边最多可能连续出现s个0，我们将无理数ξ以二进制方式展开到小数点后s+m位，再将最左边的s个bit截取掉，剩下m个bit作为随机数。我们用软件方法进行原理验证时，s的值取64，m的值取10⁶。最终得到长度为10⁶的二元序列作为随机数。我们在计算机上用这种方法生成了多组长度为10⁶的二元序列，全部通过了国家密码管理局《随机性检测规范》规定的所有15项检测。

本发明基于连分数理论，利用无理数连分数展开的渐近分数对无理数进行有理逼近来产生随机数。只要用物理方法产生的随机数是真随机数，即使随机数源的随机性很差，用本发明的方法进行处理后也能得到通过国家密码管理局《随机性检测规范》规定的所有15项检测的高性能随机数。

附图说明

图1为随机数生成流程示意图。

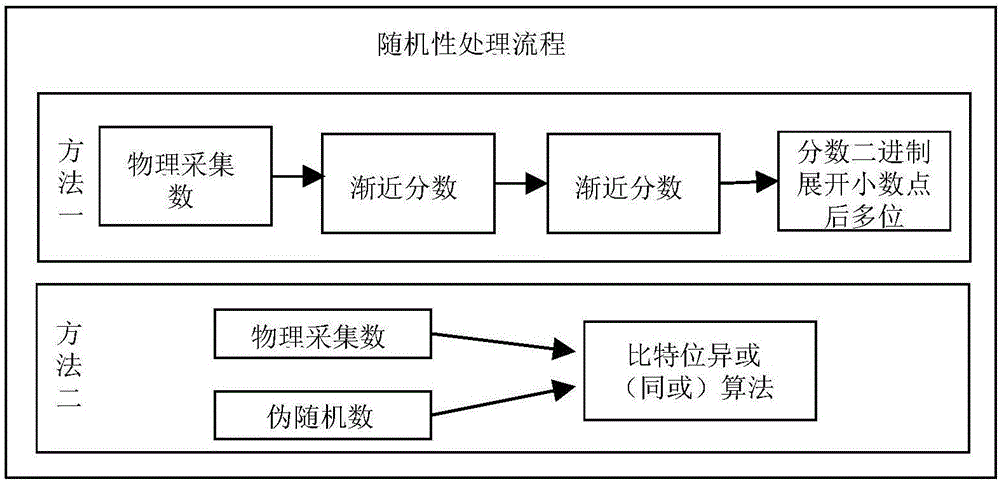
图2为随机性处理流程示意图。

图3为本发明的结果示意图。

图4是本发明得第一种结构示意图。

图5是本发明的第二种结构示意图。

具体实施方式

实施例1

参见图1、图2、图3和图4,本高性能随机数发生方法，包括以下步骤：

首先，通过物理数据采集模块生成随机性较差的随机数，所述性能较差的随机数为原始随机数；

其次，通过随机性算法处理模块对原始随机数进行随机性算法处理以得到真随机数。

作为优选方案，所述随机性算法处理模块对原始随机数进行有理数逼近无理数的算法变换；所述算法变换首先得到渐近分数，然后对渐近分数使用大整数除法得到结果，再将结果进行二进制展开，最终得到高随机性的随机序列。

或者如图5所示，通过伪随机数生成芯片生成随机性较好的伪随机数；通过随机性算法处理模块对原始随机数与随机性很好的伪随机数进行按位异或，最终得到高随机性的真随机数。所述随机性算法处理模块对原始随机数与随机性很好的伪随机数进行按位异或后，接着对异或结果按位取反，最终得到高随机性的真随机数。进一步的，所述伪随机数生成模块使用伪随机数算法得到随机性很好的伪随机数；最后使用伪随机数比特位0或1，按位决定物理采集数对应的比特位是否翻转，最终得到高随机性的真随机数。

实施例2

本高性能随机数发生方法，包括以下步骤：

首先物理采集随机数，将该随机性较差的随机数以每s个bit进行截取；每s个bit代表一个s位的二进制无符号整数，依次作为连分数的部分商x₁,…,x_n,…，置x₀＝0；无限连分数＜x₀，...，x_n，...＞一定收敛于一个无理数ξ；

因为x₀＝0，所以无理数ξ的小数点左边恒为0，用小数点右边的二进制展开作为随机数；

用循环语句依次计算无理数ξ的每个渐近分数，用条件k_nk_n+1≥2^m作为循环终止的条件；

循环终止后，利用渐近分数可以将无理数ξ以二进制方式展开到小数点后m位；由于小数点右边最多可能连续出现s个0，将无理数ξ以二进制方式展开到小数点后s+m位，再将最左边的s个bit截取掉，剩下m个bit作为随机数。

s、n、m都可以取任意长，s取32或64，m取1万到10万之间；n由m通过计算决定，满足k_nk_n+1≥2^m。参见图1，利用物理特性产生真随机数芯片输出随机数，经过随机性处理过程，最终产生高性能随机数。参见图2，随机性处理过程后，使用大整数逼近无理数算法，最终输出高性能随机数。

实施例3

参见图1、图2、图3和图4,本高性能随机数发生器，包括用于生成随机性能较差的随机数的物理数据采集模块，所述性能较差的随机数为原始随机数；还包括用于对原始随机数进行随机性算法处理以得到真随机数的随机性算法处理模块。所述随机性算法处理模块用于对原始随机数进行有理数逼近无理数的算法变换；所述算法变换首先得到渐近分数，然后对渐近分数使用大整数除法得到结果，再结果进行二进制展开，最终得到高随机性的随机序列。

或者如图5所示，还包括伪随机数生成芯片，所述伪随机数生成芯片用于生成随机性较好的伪随机数；所述随机性算法处理模块用于对原始随机数与随机性很好的伪随机数进行按位异或，最终得到高随机性的真随机数。所述随机性算法处理模块对原始随机数与随机性很好的伪随机数进行按位异或后，接着对异或结果按位取反，最终得到高随机性的真随机数。所述伪随机数生成模块使用伪随机数算法得到随机性很好的伪随机数；最后使用伪随机数比特位0或1，按位决定物理采集数对应的比特位是否翻转，最终得到高随机性的真随机数。