模态能量法中模态间耦合强度的一种界定方法与流程

本发明属于耦合系统间耦合强度的界定方法领域，具体涉及模态能量法中模态间耦合强度的一种界定方法。

背景技术：

声振问题广泛存在于航空、航天、船舶、车辆等领域。为解决声振问题，大量声振响应分析方法被提出。模态能量法是近几年被提出、发展的一种基于能量的声振响应分析方法。模态能量法基于能量守恒原理，通过推导，获得了系统中所有模态上的单频功率流平衡方程，进而求解获得每一阶模态的单频振动能量响应。相比于经典的两种能量分析方法——统计能量法和统计模态能量分布分析方法，模态能量法可以获得系统声振响应在频域内较详细的分布情况。详细的声振响应分析结果更有利于指导设计人员设计声振系统。

在模态能量法中，不同模态间的耦合强度不同。当模态间耦合强度较弱时，模态上载荷的输入功率可采取简化计算措施以提高分析效率；当模态间耦合强度较强时，对模态输入功率采取简化计算会引起较大分析误差。因此，在模态能量法理论框架中，需要有一个模态间耦合强度的界定方法，以明确模态输入功率简化措施的适用范围。

技术实现要素：

发明目的：为了克服现有技术中存在的不足，本发明提供一种模态能量法中模态间耦合强度的一种界定方法，该方法可用于明确模态能量法中模态输入功率简化措施的适用范围。

技术方案：为实现上述目的，本发明采用的技术方案为：

一种模态能量法中模态间耦合强度的一种界定方法，包括以下步骤：

(1)根据模态参数确定两个耦合模态间的临界陀螺耦合系数γ^crit(ω)、陀螺耦合系数γ；

(2)根据所述临界陀螺耦合系数和陀螺耦合系数确定两个耦合模态间的耦合强度系数κ；

(3)根据模态参数确定两个耦合模态间的临界强度系数κ^crit；

(4)根据所述耦合强度系数和临界强度系数确定两个耦合模态间的耦合强度；

(5)确定模态输入功率简化措施的适用范围。

进一步的，所述步骤(1)中的两个模态中只有一个模态直接受到外载荷激励，为板位移模态，另一个间接受到载荷激励，为声腔声压模态；两个耦合模态间的临界陀螺耦合系数为：

其中Δ_d＝η_dω_d，Δ_i＝η_iω_i，ω_d、η_d分别为直接受到载荷激励的模态的固有频率与阻尼系数，ω_i、η_i分别为间接受到载荷激励的模态的固有频率与阻尼系数；ω为角频率。

进一步的，所述步骤(1)中的两个耦合模态间的陀螺耦合系数为：

或

其中M_d为直接受到激励的模态的模态质量，M_i为间接受到激励的模态的模态质量，W_d、p_d分别为直接受到激励的模态的位移振型和应力振型，W_i、p_i分别为间接受到激励的模态的位移振型和应力振型，S为耦合面。

进一步的，所述步骤(2)中两个耦合模态间的耦合强度系数κ为：

κ＝|γ|/γ^crit(ω_i)，

其中，

其中Δ_d＝η_dω_d，Δ_i＝η_iω_i，ω_d、η_d分别为直接受到载荷激励的模态的固有频率与阻尼系数，ω_i、η_i分别为间接受到载荷激励的模态的固有频率与阻尼系数。

进一步的，所述步骤(3)中两个耦合模态间的临界强度系数κ^crit由下式确定：

其中，T＝100·|Log₁₀(ω_i/ω_d)|，

进一步的，所述步骤(4)中两个耦合模态间的耦合强度由下述方法确定：

当κ≤κ^crit时，两个模态间为弱耦合；

当κ^crit＜κ≤1时，两个模态间为温和耦合；

当κ＞1时，两个模态间为强耦合。

进一步的，所述步骤(5)中当模态间的耦合为弱耦合时，模态输入功率简化措施适用。

进一步的，模态输入功率简化措施表述如下：

模态输入功率的精确计算方法为：

其中，S_d(ω)为模态力自功率谱，G_d(ω)为在耦合系统中模态上激励的输入导纳；采用非耦合模态上激励的输入导纳代替耦合系统中模态上激励的输入导纳G_d(ω)，由下式给出：

其中，Re(·)表示复数的实部；j表示复数的虚部。

进一步的，所述步骤(1)中的模态能量法的单频功率流平衡方程为：

其中，α_mn(ω)为模态m对模态n的单频耦合损耗因子，α_nm(ω)为模态n对模态m的单频耦合损耗因子，为模态损耗功率，为模态输入功率，E_m(ω)、E_n(ω)分别为模态m和模态n的单频振动能量；

α_mn(ω)与α_nm(ω)的表达式具有对称性，α_mn(ω)由下式给出：

其中，Δ_m＝η_mω_m，Δ_n＝η_nω_n，ω_m、ω_n分别为模态m和模态n的固有频率，η_m、η_n分别为模态m和模态n的阻尼系数，ω为角频率，模态m和模态n间的陀螺耦合系数为：

或

其中，M_m、M_n分别为模态m和模态n的模态质量，W_m、p_m分别为模态m的位移振型和应力振型，W_n、p_n分别为模态n的位移振型和应力振型，S为耦合面。

进一步的，所述模态损耗功率为：

有益效果：本发明提供的模态能量法中模态间耦合强度的一种界定方法，该方法确定了模态输入功率简化措施的适用范围，为设计人员在选取模态输入功率的计算方法时提供依据，在一定程度上提高分析效率的同时确保了结果的可靠性。

附图说明

图1为本发明的逻辑流程框图；

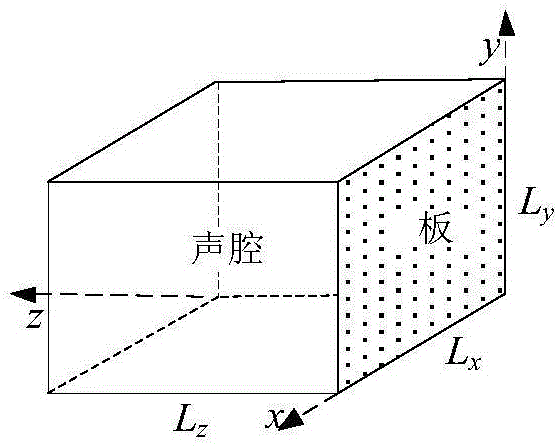
图2是一个矩形简支板与长方体声腔耦合系统的示意图；

图3是板位移模态与声腔声压模态间的耦合强度系数示意图；

图4是耦合强度系数与临界强度系数间的比值示意图；

图5是声腔总振动能量示意图。

具体实施方式

下面结合附图对本发明作更进一步的说明。

如图1所示为本发明的方法的逻辑流程图，主要包括5个步骤，具体的方法过程如下：

一种模态能量法中模态间耦合强度的一种界定方法，包括以下步骤：

(1)根据模态参数确定两个耦合模态间的临界陀螺耦合系数γ^crit(ω)、陀螺耦合系数γ：

(1.1)两个模态中只有一个模态直接受到外载荷激励，为板位移模态，另一个间接受到载荷激励，为声腔声压模态；两个耦合模态间的临界陀螺耦合系数为：

其中Δ_d＝η_dω_d，Δ_i＝η_iω_i，ω_d、η_d分别为直接受到载荷激励的模态的固有频率与阻尼系数，ω_i、η_i分别为间接受到载荷激励的模态的固有频率与阻尼系数；ω为角频率。

(1.2)两个耦合模态间的陀螺耦合系数为：

或

其中M_d为直接受到激励的模态的模态质量，M_i为间接受到激励的模态的模态质量，W_d、p_d分别为直接受到激励的模态的位移振型和应力振型，W_i、p_i分别为间接受到激励的模态的位移振型和应力振型，S为耦合面。

(1.3)模态能量法的单频功率流平衡方程为：

其中α_mn(ω)为模态m对模态n的单频耦合损耗因子，α_nm(ω)为模态n对模态m的单频耦合损耗因子，为模态损耗功率，为模态输入功率，E_m(ω)、E_n(ω)分别为模态m和模态n的单频振动能量；

模态损耗功率为：

α_mn(ω)与α_nm(ω)的表达式具有对称性，α_mn(ω)由下式给出：

其中，Δ_m＝η_mω_m，Δ_n＝η_nω_n，ω_m、ω_n分别为模态m和模态n的固有频率，η_m、η_n分别为模态m和模态n的阻尼系数，ω为角频率，模态m和模态n间的陀螺耦合系数由下式给出：

或

其中，M_m、M_n分别为模态m和模态n的模态质量，W_m、p_m分别为模态m的位移振型和应力(声压)振型，W_n、p_n分别为模态n的位移振型和应力(声压)振型，S为耦合面。

(2)根据所述临界陀螺耦合系数和陀螺耦合系数确定两个耦合模态间的耦合强度系数κ：

两个耦合模态间的耦合强度系数κ为：

κ＝|γ|/γ^crit(ω_i)，

其中，

其中Δ_d＝η_dω_d，Δ_i＝η_iω_i，ω_d、η_d分别为直接受到载荷激励的模态的固有频率与阻尼系数，ω_i、η_i分别为间接受到载荷激励的模态的固有频率与阻尼系数；

(3)根据模态参数确定两个耦合模态间的临界强度系数κ^crit：具体包括：

(3.1)定义无量纲参数T为：

T＝100·|Log₁₀(ω_i/ω_d)|

(3.2)两个耦合模态间的临界强度系数κ^crit由下式确定：

其中

(4)根据所述耦合强度系数和临界强度系数确定两个耦合模态间的耦合强度：由下述方法确定：

当κ≤κ^crit时，两个模态间为弱耦合；

当κ^crit＜κ≤1时，两个模态间为温和耦合；

当κ＞1时，两个模态间为强耦合。

(5)确定模态输入功率简化措施的适用范围：当模态间的耦合为弱耦合时，上述模态输入功率简化措施引起的误差可忽略，模态输入功率简化措施适用。模态输入功率简化措施表述如下：

模态输入功率的精确计算方法为：

其中，S_d(ω)为模态力自功率谱，G_d(ω)为在耦合系统中模态上激励的输入导纳；采用非耦合模态上激励的输入导纳代替耦合系统中模态上激励的输入导纳G_d(ω)，由下式给出：

其中，Re(·)表示复数的实部；j表示复数的虚部。

实施例

如图2所示为一个矩形简支板与长方体声腔耦合系统的示意图。本实施例中简支板的尺寸为：x轴向长度L_x＝1m，y轴向长度L_y＝1m，厚度h＝0.01m。矩形简支板所用材料的参数为：弹性模量E＝120GPa，材料密度ρ_p＝7800kg/m³，泊松比υ＝0.3，阻尼η_p＝0.01。长方体声腔的尺寸为：：x轴向长度L_x＝1m，y轴向长度L_y＝1m，z轴向长度L_z＝1m。长方体声腔中空气的材料属性为：密度ρ_c＝1.29kg/m³，声速c₀＝340m/s，阻尼η_c＝0.01。本实施例中只有简支板直接受到外载荷激励。

步骤(1)：确定任意一阶板位移模态与任意一阶声腔声压模态之间的临界陀螺耦合系数为：

其中Δ_s＝η_sω_s，Δ_a＝η_aω_a，ω_s、η_s分别为直接受到载荷激励的板位移模态的固有频率与阻尼系数，ω_a、η_a分别为间接受到载荷激励的声腔声压模态的固有频率与阻尼系数。

步骤(2)：确定任意一阶板位移模态与任意一阶声腔声压模态之间的耦合强度系数，具体包含以下步骤：

步骤(2.1)：确定板位移模态与声腔声压模态间的陀螺耦合系数为：

其中M_s、W_s分别为直接受到载荷激励的板位移模态的模态质量及振型，M_a、W_a分别为间接受到载荷激励的声腔声压模态的模态质量及振型，S为耦合面。

(2.2)：确定板位移模态与声腔声压模态间的耦合强度系数为：

κ＝|γ|/γ^crit(ω_a)

其中

如图3所示为本实施例中板位移模态与声腔声压模态间的耦合强度系数。

步骤(3)：确定任意一阶板位移模态与任意一阶声腔声压模态之间的临界强度系数，具体包含以下步骤：

步骤(3.1)：定义无量纲参数T为：

T＝100·|Log₁₀(ω_a/ω_s)|

步骤(3.2)：确定板位移模态与声腔声压模态间的临界强度系数κ^crit由下式确定：

其中

如图4所示为本实施例中模态间耦合强度系数与临界强度系数之间的比值。

步骤(4)：确定板位移模态与声腔声压模态间的耦合强度：当κ≤κ^crit时，两个模态间为弱耦合；当κ^crit＜κ≤1时，两个模态间为温和耦合；当κ＞1时，两个模态间为强耦合。图3中结果显示，本实施例中，只有三对模态间为强耦合，其余模态间均为弱耦合或温和耦合。图4中结果显示，本实施例中，许多落在区域I内的低阶模态间有κ/κ^crit＞1，结合图3中结果可判定这些低阶模态间为温和耦合，几乎所有落在区域II内的高阶模态间有κ/κ^crit≤1，即κ≤κ^crit，因此这些高阶模态间为弱耦合。

步骤(5)：确定板位移模态上载荷输入功率简化措施的适用范围。模态输入功率的精确计算方法为：

上式中S_s(ω)为模态力自功率谱，G_s(ω)为在耦合系统中板位移模态上激励的输入导纳。为简化计算，采用非耦合的板位移模态上激励的输入导纳代替耦合系统中板位移模态上激励的输入导纳G_d(ω)，由下式给出：

其中Re(·)表示复数的实部。

如图5所示为本实施例中由模态能量法计算获得的声腔总振动能量。其中“近似解”为对模态上载荷输入功率采取简化措施后的声腔振动能量计算结果。图5中结果显示，在1006Hz之后的频段内，“近似解”具有足够的精度。结合图4及图5中的结果可知，当模态间为弱耦合时，板位移模态上的载荷输入功率简化措施所引起的误差可忽略。

现有的耦合强度界定方法将κ^crit＜κ≤1的情况划分为弱耦合，同时认为弱耦合时，板位移模态上的载荷输入功率简化措施所引起的误差可忽略；而图5中结果显示，在κ^crit＜κ≤1时，分析误差达到4.7dB，不可忽略。本发明将κ^crit＜κ≤1的情况划分为温和耦合，同时认为温和耦合时，板位移模态上的载荷输入功率简化措施所引起的误差不可忽略，与本实施例所得结果相符。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。