一种砂轮圆弧修整廓形在线测量方法与流程

本发明涉及一种砂轮圆弧修整廓形在线测量方法。

背景技术：

汽车曲轴作为发动机关键零件，其主轴颈、连杆颈巴厘线(即曲轴轴颈圆柱表面母线具有一定公差要求的圆弧形)的磨削精度对发动机性能有较大影响。由于巴厘线通常采用砂轮进行成形修整后进行切入磨实现，其磨削精度主要靠砂轮廓形精度保证。因此对砂轮圆弧修整实际廓形的检测极其重要。对于砂轮实际修整廓形的测量，传统方法大多采用离线测量：要么修整后将砂轮拆下进行直接测量，要么将廓形复刻至石墨或工件上后进行间接测量。这些方法费时费力，并不适用于高效率大批量的现代化汽车曲轴生产线中。

随着传感器技术的发展，声发射(Acoustic Emission,AE)信号因其高频的特点，可避开低频噪声的干扰且灵敏度极高，已被广泛应用于对工件磨削及砂轮修整过程的监测。因此，若能建立声发射信号与修整切深的数学模型，实现利用声发射传感器进行砂轮修整廓形的在线间接测量，就能够进一步实现在线误差补偿，能在保证修整精度的同时大大提高修整效率，也有利于提高曲轴生产效率。

技术实现要素：

本发明的目的在于针对现有技术的不足，而提供一种砂轮圆弧修整廓形在线测量方法。该方法利用声发射传感器对砂轮修整过程进行在线监测，通过建立砂轮圆弧修整过程中各位置声发射信号特征值与实际修整切深的数学模型，实现基于声发射信号的砂轮圆弧修整廓形的在线测量。从而能够通过高效率的在线测量及时进行误差补偿，实现砂轮圆弧修整廓形精度控制。

为了达到上述目的，本发明的构思是：通过布置在修整器附近的声发射传感器及相关采集设备实时获取砂轮修整过程中的声发射信号；在滤波等信号预处理的基础上，基于某位置附近微小时段声发射信号均方根值与该位置实际修整切深之间的数学模型，对砂轮实际修整廓形进行在线估计，从而实现砂轮圆弧修整廓形的在线测量。

本发明所用的砂轮圆弧修整廓形在线测量系统包括声发射传感器、磁性基座、前置放大器、采集卡、机箱、计算机。其特征在于声发射传感器利用磁性基座吸附在修整器附近，在不产生干涉的前提下尽量靠近修整点，其安装高度与修整器修整点及砂轮轴线等高，安装面与声发射波传播方向垂直。

根据上述构思，本发明采用以下技术方案：

一种砂轮圆弧修整廓形在线测量方法，其步骤如下：

1)输入修整参数：进给速度(也称切向进给速度)F、修整圆弧中凸量a_p。

2)进行砂轮廓形测量系统标定，明确砂轮圆弧修整过程中各位置声发射信号均方根值X_ae与修整切深X_gr的数学模型。

3)根据修整过程特点设置AE信号采样频率，根据圆弧中凸量a_p和圆弧宽度d计算砂轮圆弧修整程序中的理论圆弧半径值r。

4)将砂轮修平。

5)运行砂轮圆弧修整程序，实时获取AE信号，利用快速傅里叶变换(FFT)进行滤波处理，并判断修整起始点位置。

6)根据修整位置与修整时间的对应关系，实时计算修整过程中各位置附近某微小时段的AE信号均方根值X_ae以及该位置的Z方向进给速度F_z。

7)将修整过程中各位置的AE信号均方根值X_ae以及该位置的Z方向进给速度F_z代入砂轮圆弧修整变参数模型，得到该位置的修整切深X_gr。

8)判断修整终点，即获得整个修整过程中的砂轮修整廓形。

上述步骤2)中砂轮廓形测量系统标定方法如下：

a)进行几组不同修整参数的砂轮圆弧修整，采集修整过程中AE信号值，计算各位置的AE信号均方根值，并将修整后的砂轮廓形进行离线测量。

b)根据AE信号均方根值与实际切深的基本数学模型(见式(1))，将几组修整条件及结果作为样本输入进行参数辨识，基于最小二乘法的原则对各参数进行拟合求解。

其中X_gr为修整切深，X_ae为AE信号均方根值，F_z为Z方向进给速度，b_i为模型参数，i＝0,1,2。

c)将模型参数b_i按如下函数进行拟合，求解出各拟合参数B_i、μ_i、σ_i、c_i。

其中F为切向进给速度，为Z方向进给速度与X方向进给速度的合成；a_p为修整圆弧中凸量；B_i为4×4矩阵，i＝0,1,2。

d)将辨识后的参数及原试验数据重新输入模型，计算所得廓形中凸量a_p估计与离线测量所得廓形中凸量a_p测量的相对误差δ_pre。

e)将误差全补偿至常系数项得到新的参数值。

其中j表示参数调整次数，j＝0,1,2,…，b₀(0)、b₁(0)、b₂(0)为初步拟合得到的参数。

f)对新参数值继续进行拟合，重复步骤c)～e)，直至模型所得廓形中凸量与离线测量所得廓形中凸量误差小于生产要求设定值，即完成砂轮圆弧修整廓形测量系统的标定，明确了砂轮圆弧修整过程中各位置声发射信号均方根值与修整切深的数学模型。

上述步骤3)中根据圆弧中凸量a_p和圆弧宽度d计算砂轮圆弧修整程序中的理论圆弧半径值r的方法如下：

上述步骤6)中各位置附近微小时段的AE信号均方根值以及该位置的Z方向进给速度F_z计算方法如下：

a)根据图2中圆弧运动特点，计算各时刻t与其所对应位置z_i的关系为

其中F为切向进给速度，为Z方向进给速度与X方向进给速度的合成；r为修整圆弧理论半径；d为修整圆弧宽度。

b)计算各时刻AE信号均方根值X_ae(t)，并根据式(6)将其转换为对应位置的AE信号均方根值。

其中V(t)为任意时刻滤波后的AE信号值，T为时间常数。

c)根据图2中几何关系及运动关系，计算可得各位置Z方向的进给速度

其中F为切向进给速度，为Z方向进给速度与X方向进给速度的合成；r为修整圆弧理论半径；d为修整圆弧宽度。

本发明与现有技术相比较，具有如下显而易见的突出实质性特点和显著优点：

本发明提供了一种利用声发射传感器间接在线测量砂轮圆弧修整廓形的方法，标定后不必采用繁琐的离线测量，在保证测量精度的同时，大大缩短了测量时间，有利于在快节奏大批量的曲轴生产中提高加工效率。

附图说明

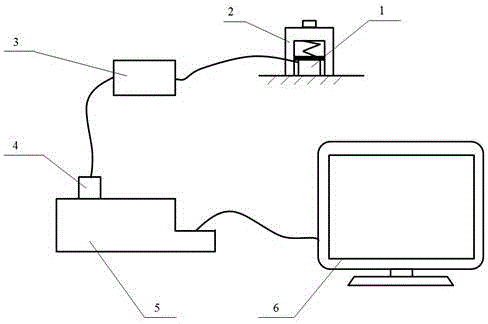
图1是本发明砂轮圆弧修整廓形在线测量系统示意图。

图2是本发明中砂轮圆弧修整几何示意图。

图3是本发明砂轮圆弧修整廓形在线测量流程图。

图4是本发明砂轮圆弧修整廓形在线测量系统标定流程。

具体实施方式

本发明的优选实施例结合附图说明如下：

参见图1，砂轮圆弧修整廓形在线测量系统包括声发射传感器1、磁性基座2、前置放大器3、采集卡4、机箱5、计算机6。声发射传感器1利用磁性基座2吸附在修整器附近，在不产生干涉的前提下尽量靠近修整点，其安装高度与修整器修整点及砂轮轴线等高，安装面与声发射波传播方向垂直；声发射信号经前置放大器3、采集卡4、机箱5采集至计算机6上，经滤波处理后即可获得修整过程中的声发射信号值。

参见图3，砂轮圆弧修整廓形在线测量方法是：

1)输入修整参数：进给速度(也称切向进给速度)F＝80mm/min、修整圆弧中凸量a_p＝1μm。

2)参见图4，进行砂轮廓形测量系统标定，明确砂轮圆弧修整过程中各位置声发射信号均方根值与修整切深的数学模型。具体方法如下：

a)分别进行几组不同修整参数的砂轮圆弧修整，具体修整条件见表1；采集修整过程中AE信号值，计算各位置的AE信号均方根值，并将修整后的砂轮廓形进行离线测量。

b)根据AE信号均方根值与实际切深的基本数学模型(见式(9))，将几组修整条件及结果作为样本输入进行参数辨识，基于最小二乘法的原则对各参数进行拟合求解。

其中X_ae为AE信号均方根值，F_z为Z方向进给速度，b_i为模型参数，i＝0,1,2。参数辨识结果见表1。

c)将模型参数b_i按如下函数进行拟合，求解出各拟合参数B_i、μ_i、σ_i、c_i。

其中F为切向进给速度，为Z方向进给速度与X方向进给速度的合成，a_p为修整圆弧中凸量，B_i为4×4矩阵，i＝0,1,2。

d)将辨识后的参数及原试验数据重新输入模型，计算所得廓形中凸量a_p估计与离线测量所得廓形中凸量a_p测量的模型估计相对误差δ_pre，计算方法见式(11)，结果见表1。

e)将误差全补偿至常系数项得到新的参数值，计算方法见式(12)，结果见表1。

其中j表示参数调整次数，j＝0、1、2、……。其中b₀(0)、b₁(0)、b₂(0)为初步拟合得到的参数。

表1砂轮廓形测量系统标定试验

f)对新参数值继续进行拟合，重复步骤c)～e)，直至模型所得廓形中凸量与离线测量所得廓形中凸量误差小于生产要求设定值±10％，即完成砂轮圆弧修整廓形测量系统的标定。最终得砂轮圆弧修整过程中各位置声发射信号均方根值与修整切深的数学模型为：

3)根据修整过程特点设置AE信号采样频率为1MHz，根据圆弧中凸量a_p＝1μm以及圆弧宽度d＝8mm计算砂轮圆弧修整程序中的理论圆弧半径值r，计算方法如下：

4)将砂轮修平。

5)运行砂轮圆弧修整程序，实时获取AE信号，利用快速傅里叶变换(FFT)进行滤波处理，并判断修整起始点位置。

6)参见图2，(7)为修整器，(8)为砂轮。根据修整位置与修整时间的对应关系，实时计算修整过程中各位置附近某微小时段的AE信号均方根值X_ae以及该位置的Z方向进给速度F_z。以修整时间t＝3s时对应的修整位置为例，具体计算方法如下：

a)根据图2中圆弧运动特点，计算各时刻t与其所对应位置z_i的关系为

其中F＝80mm/min为切向进给速度，为Z方向进给速度与X方向进给速度的合成；修整圆弧理论半径r＝8000.0005mm；修整圆弧宽度d＝8mm。代入式(15)中计算得各时刻t与其所对应位置z_i的关系为

修整时间t＝3s时，对应修整位置z_i为

b)计算该时刻AE信号均方根值，并根据修整时间与修整位置的对应关系将其转换为对应位置的AE信号均方根值。

其中V(t)为任意时刻滤波后的AE信号值，T＝0.1s为时间常数。经采集计算得到该位置的AE信号均方根值为X_ae＝0.4641V。

c)根据图2中几何关系及运动关系，计算可得各位置Z方向的进给速度F_z，计算方法如下：

其中，进给速度F＝80mm/min，修整圆弧宽度d＝8mm，修整圆弧理论半径r＝8000.0005mm；由上述步骤a)得修整时间t＝3s时的对应修整位置为z_i＝4mm，则该位置Z方向进给速度F_z为

7)将上述过程计算所得的修整过程中该位置AE信号均方根值X_ae、Z方向进给速度F_z以及修整参数(进给速度F、圆弧中凸量a_p)代入模型，得到该位置的修整切深X_gr。

本实例中进给速度F＝80mm/min，圆弧中凸量a_p＝1μm；由上述步骤6)得修整时间t＝3s时的对应修整位置为z_i＝4mm，该位置处的AE信号均方根值X_ae＝0.4641V，Z方向进给速度F_z＝80mm/min。将其代入式(13)，可得该位置的修整切深X_gr为：

8)判断修整终点，即获得整个修整过程中的砂轮修整廓形。