一种产品故障行为耦合建模和可靠性评估方法与流程

本发明提出了一种产品故障行为耦合建模和可靠性评估方法，特别是涉及一种基于藤-卡普拉(Vine-Copula)和加速退化试验的产品故障行为耦合建模和可靠性评估方法，属于可靠性技术领域中的故障行为建模。

背景技术：

航天、航空、核设备、电力网络等重大装备的安全服役对于国民经济发展和国防建设都具有重要意义，但其运行条件复杂、环境恶劣，容易导致恶性事故发生，因此正确认识故障、评估和预测其可靠性对于保证设备安全运行、提高经济效益有很大的意义。由于系统复杂度的提高以及对于故障认识的深入，针对可靠性理论的研究，已逐步从面向“故障时间”转向面向“故障过程”。基于故障过程的研究一方面是从微观的角度出发研究故障发生机理，即故障物理学。另一方面是从宏观角度出发，研究故障的发生发展及在系统中的传播，即故障的行为。该发明基于Vine-Copula和加速退化试验的产品故障行为耦合建模和可靠性评估方法是一种对具有多元变量的产品故障行为建模及可靠性评估方法。通过对现有技术的查新，国内外还没有基于Vine-Copula和加速退化试验对产品进行故障行为耦合建模和可靠性评估方面的研究。

技术实现要素：

针对高可靠长寿命复杂产品具有故障机理耦合的特点，在构建宏观故障行为模型进行可靠性评估的方面，提出了一种基于Vine-Copula和加速退化试验的具有多元变量产品故障行为建模及可靠性评估方法。该方法一方面可以清楚描述产品多元变量耦合关系，另一方面可以在可承受时间和成本内进行产品可靠性评估。

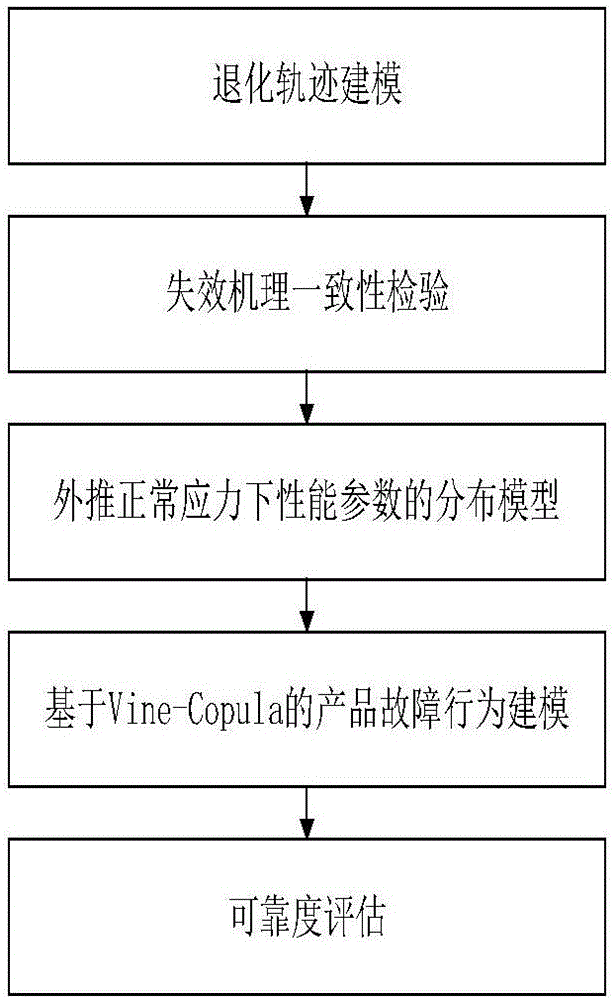
本发明在进行产品故障行为耦合建模和可靠度评估之前，需明确组成产品的系统的故障行为描述方法，选定描述系统故障行为的表征量。由于组成系统的部件之间的故障机理相互影响会表现在部件的状态上，一种可用的方法是采用部件的状态向量Z(t)为表征，描述系统的故障行为，构建故障行为耦合模型,从而估计系统的可靠度。其中，Z(t)＝(D(t)，X(t)，F(t))^T，D(t)是部件损伤状态变量，X(t)是部件响应变量，F(t)是部件承受的应力变量。对于系统而说，各部件间或者部件内部存在的机理竞争或者耦合问题可以用每个部件的状态向量中的损伤状态变量表示其退化损伤状况来构建产品故障行为耦合模型；而从实际角度，损伤状态变量一般从产品的监测参数上来反应，因此本发明从加速退化试验下各水平的性能参数试验数据入手，进行建模与分析，具体实施流程见附图1。

本发明是采用以下技术方案实现的，本发明一种产品故障行为耦合建模和可靠性评估方法，即一种基于Vine-Copula和加速退化试验的产品故障行为耦合建模和可靠性评估方法，其步骤如下：

步骤一：退化轨迹建模

产品的退化轨迹模型可表示为退化量与时间及所受环境应力的函数；在进行退化轨迹建模时，需

1.分析退化数据特点，建立退化轨迹模型Δy_t＝f(t,S)，Δy_t表示t时刻的退化量，S表示所受环境应力水平大小；

2.建立似然函数f_i表示第i个退化量测试点的概率密度函数，μ，σ表示退化轨迹模型参数；

3.代入退化数据，利用Nelder-Mead单纯形法对似然函数的极大值问题进行求解，得到各应力水平下各性能参数退化轨迹模型的参数估计；

步骤二：失效机理一致性检验

在加速退化试验中，为保证试验的有效性，不同加速应力水平下的同一性能参数应符合失效机理一致性检验。退化轨迹建模中模型参数与失效机理不变间存在的联系依据退化轨迹建模方法的不同而存在差别，以服从漂移布朗运动的退化轨迹建模为例：

1.确定其加速机理一致性检验公式其中μ_i和σ_i分别为应力水平S_i下的退化轨迹模型的漂移系数与扩散系数；

2.构建假设检验统计量T从自由度为n+m-2的t分布；其中：X服从均值为μ₁方差为σ²的正态分布,Y服从均值为μ₂方差为σ²的正态分布,且X₁，X₂，…X_n是来自总体X的样本，Y₁,Y₂,…Y_m是取自总体Y的样本，n和m分别为样本量大小；

3.确定拒绝域。给定显著性水平α，代入数据计算|T|，查t分布表可知：t_1-α/2(n+m-2)的大小，若|T|≥t_1-α/2(n+m-2)，则检验结果落在拒绝域内，参数在不同应力下的失效机理不具有一致性。反之，则满足一致性检验；

步骤三：外推正常应力下性能参数的分布模型

产品寿命特征与加速应力水平之间的关系可通过加速模型来表述，利用加速模型可推导得到正常应力下各变量的退化模型及边缘分布；本发明中，采用简化的多应力艾琳加速模型：t为特征寿命，T和RH分别表示温度与湿度变量，A、B和C为待求参数；

1.确定加速因子

令AF_i,0＝t₀/t_i为加速应力水平S_i相对于正常应力水平S₀的加速因子，t_i和t₀分别表示产品在加速应力水平S_i与正常应力水平S₀下，性能参数达到相同退化量时所需要的时间；

2.求解加速模型参数

a.构建加速因子与不同应力间寿命、漂移系数、扩散系数的关系等式其中AF表示加速因子，L表示寿命，μ_i和σ_i表示在加速应力S_i下性能参数退化轨迹的漂移系数和扩散系数；下标h表示较高的应力水平下，下标l表示较低的应力水平下；

b.对性能参数p，在k₁和k₂应力水平下，构造离差平方和函数采用Nelder-Mead单纯形法对离差平方和函数的极小值问题进行求解，得到加速模型中最优模型参数B、C；

3.估计正常应力下退化轨迹模型参数

求得加速模型中的参数之后，使用最小二乘法对正常应力下退化轨迹模型参数进行估计，得到离差平方和函数与采用单纯形法求解使离差平方和最小所对应的参数值，从而得到正常应力下退化轨迹模型参数μ_p0和σ_p0的点估计；最终正常应力下退化轨迹模型为：y_p0(t)＝μ_p0t+σ_p0B(t)；

步骤四：基于Vine-Copula的产品故障行为耦合建模

Copula函数是一类“连接”函数，连接的是边缘分布与联合分布。Vine-Copula的理论基础是条件概率，通过将联合分布分解成多个二元copula及相应的条件概率连乘的形式进行建模，基于Vine-Copula的产品故障行为耦合建模主要流程如下：

1.性能参数相关性分析

在进行产品的故障行为耦合建模前，对于产品的多元性能参数退化，要先进行相关性分析；用Kendall’sτ系数作为相关性度量指标，指标的绝对值越接近1表示相关性越强，且Kendall’sτ系数表示非线性相关程度；

2.借助vine图模型将联合分布分解为合适的条件概率相乘的形式，利用copula函数构建多元相关关系模型；具体，

a.基于D-Vine的建模方法

1)首先，在第一层Vine图模型中，各变量作为树图中的节点，节点之间按相互关系用短线进行连接，例如，一种四维的D-vine其第一层关系如附图2所示。以c_ij表示连接节点i与节点j的copula函数的概率密度，则c_ij＝c_pq，p、q分别为节点i和节点j包含的变量。

2)Vine图中的第二层树图建立在第一层树图的基础上，以第一层树图中的连接作为第二层树图中的节点，第一层中相邻的连线在第二层的形成的元用连线进行连接，构建第二层的树图，例如附图3是以附图2中(1,2)、(2,3)、(3,4)为元建立第二层树图。仍以c_ij表示连接节点i与节点j的copula函数的概率密度，有c_ij＝c_pq|k，{p,k}、{q,k}分别为节点i和节点j包含的变量，其中k为两节点共有的变量。

3)第三层树图也是采用类似的方法在前一层树图基础上进行建立，以此类推，当树图中只剩下一对相关关系，即只剩一条连线时，就是最后一层的树图了。同理，第三层树图到包括最后一层树图在内的所有连接节点之间的copula函数的概率密度都有c_ij＝c_pq|k，{p,k}、{q,k}为节点i和节点j包含的变量，其中k为两节点共有的变量。

4)将Vine图中的各条连线对应的copula函数概率密度相乘，即可得到基于Vine图的copula函数的分解结构.c＝∏c_ij。产品可靠度联合分布概率密度函数可表示为x_i表示产品的第i个性能参数，r_i表示第i个参数对应的可靠度概率密度函数,至此基于Vine-Copula耦合模型已建立。

b.求解Vine-Copula耦合模型

求解Vine-Copula耦合模型,即可靠度联合分布概率密度，要先确定可靠度联合分布概率密度r(x₁,...,x_n)中各个copula概率密度函数的形式及参数，即c_ij的形式与参数。

1)确定Vine模型中第一层树图中的c_ij:代入第i、第j个节点对应性能参数(p、q)的退化量数据。根据备选的copula函数形式建立似然函数采用Nelder-Mead单纯形法求解似然函数的极大值及其对应的copula函数参数值，然后基于AIC准则选取最为合适的copula函数形式及对应的参数。其中，似然函数L中j表示样本编号，共m个样本，i表示测试点序号，共n个测试点，R_p(t)与R_q(t)分别表示第p和q个性能参数的可靠度分布函数。

2)确定Vine模型中第二层树图中的c_ij:令{p,k}、{q,k}分别为节点i和节点j包含的变量，则有c_ij＝c_pq|k，根据备选的copula函数形式建立似然函数采用Nelder-Mead单纯形法求解似然函数的极大值及其对应的copula函数参数值，然后基于AIC准则选取最为合适的copula函数形式及对应的参数。其中，似然函数L中j表示样本编号，共m个样本，i表示测试点序号，共n个测试点，R_p|k(t)与R_q|k(t)分别表示可靠度联合分布的条件概率表达式，其计算公式遵循：

i.当k为一维变量时，即两个节点间只包含一个相同变量，此时R_p|k(t)和R_q|k(t)的值按照计算。其中R为可靠度分布函数，表示该copula函数对R_j求导。

ii.当k为维数大于1的向量时，即两个节点间包含多个相同变量，此时R_p|k(t)和R_q|k(t)的值按照计算。其中v是条件向量，v＝(v₁,v₂,...,v_d)，v_j是v中的任意一个元素，v_-j表示v除去v_j得到的向量。

确定Vine模型中第二层树图中的c_ij后，以此类推，计算其他层树图的c_ij,直至确定Vine图中所有最优的copula函数形式为止。

3)确定所有c_ij的函数形式后，对已选定的c_ij的参数一起进行再次估计。建立似然函数L＝r(x₁,...,x_n)，采用Nelder-Mead单纯形法方法求解似然函数的极大值，可得到对应的最优参数结果。将所有c_ij函数的参数回代Vine-Copula的分解式中，即得到了基于Vine-copula建立的多元相关关系模型。

步骤五：可靠性评估

利用Vine-Copula函数完成产品故障行为耦合建模后，可以得到产品的可靠度联合分布概率密度函数。然而由于Copula函数的密度函数结构复杂多样，同时各性能参数的可靠度概率密度函数表达式也十分复杂，造成可靠度联合分布的概率密度函数的解析式不仅长而且非常复杂，很难通过直接积分的方法求解可靠度函数。对于非严格单调退化情况下的产品可靠度联合分布的精确解问题，本发明采用了条件概率分解的方法进行求解。

1.计算二元变量的可靠度联合分布的条件概率表达式

其中R为可靠度分布函数，表示该copula函数对R_j求导。

2.计算多元变量可靠度联合分布的条件概率表达式

其中v是条件向量，v＝(v₁,v₂,...,v_d)，v_j是v中的任意一个元素，v_-j表示v除去v_j得到的向量，v_-j＝(v₁,v₂,...,v_j-1,v_j+1,...,v_d)。

3.计算多元可靠度联合分布表达式

其中K表示发生退化的性能参数个数，a_k是性能参数的代号，v是条件向量，v_j是条件向量v中的一个元素，v_-j表示条件向量v中除去v_j得到的向量，为v_j对应的时间，为向量v_-j中元素对应的时间构成的时间向量。

其中，在步骤四中所述的“基于AIC准则选取最为合适的copula函数形式”是指：以AIC最小值所对应的copula认为是备选copula形式中最为适宜的选择。AIC的计算式为AIC＝-2lnL+2p，其中L是极大似然函数值，p是模型参数个数，M是样本大小，对应的取值是产品的观测点个数。

其中，在步骤五中，为便于可靠度联合分布的求解，将可靠度联合分布分解为条件概率的原则是使得最终分解结果中的各项二元Copula函数尽量都是Vine-Copula中已使用并确立的二元Copula函数，所述的“条件概率分解的方法”，可以遵循一些原则：

1)分解式中首个可靠度边缘分布(即)，对于D-vine宜选择第一层两端任意的端节点；

2)分解式中第二项，即对于D-vine宜选择第二层的同侧端节点；

3)以此类推，对于D-vine宜选择相应的端节点。

通过以上步骤，完成了对产品的故障行为耦合建模，建立了可靠度联合分布的模型，解决了直接积分法求解可靠度函数的难题，清楚描述产品多元变量耦合关系，提供了在可承受时间和成本内进行产品可靠性评估的方法。

本发明的优点在于：

针对多元变量高可靠长寿命产品，基于加速退化试验数据和漂移布朗运动，在加速机理一致性检验的基础上，构建得到了正常应力水平下的变量边缘分布。基于分层思想，利用Vine-Copula方法，用二元Copula函数描述了多维联合分布的解耦问题，即对潜在的部件相关性机理进行了解耦建模，避免了多元Copula函数在高维上的数值仿真求解问题。同时，在可靠度计算方面，由于目前Copula函数的建模方法通常都是搭配严格单调退化的退化模型进行寿命评估，本发明提出的基于条件概率的求解方法使得对于非严格单调退化的情况也能求解。最后，对比多维正态分布建模方法，克服了退化参数间仅服从线性或不相关的关系，表明Vine-Copula能有效处理非线性相关下的可靠寿命估计。

附图说明

图1本发明所述方法实施流程图。

图2四维D-vine第一层树图。

图3四维D-vine第二层树图。

图4智能电表基本误差的D-vine模型。

图5智能电表四项基本误差的联合可靠度图。

图中序号、代号说明如下：

图2和图3中数字分别代表性能参数的代码。图4中BE1、BE5、BE9、BE10表示智能电表的四项基本误差，CE表示智能电表的累计误差。BE1BE5代表连接节点BE1与节点BE5的连线，表征性能参数BE1与BE5相关，并作为vine图中第二层的节点。BE5BE9和BE9BE10表征含义同上。BE1BE9|BE5代表连接节点BE1BE5与节点BE5BE9的连线，表征性能参数BE5既与BE1相关，又和BE9相关，并且BE1BE9|BE5作为vine图中第三层的节点。BE5BE10|BE9含义同上。BE1BE10|BE5BE9表示代表连接节点BE1BE9|BE5与节点BE5BE10|BE9的连线，表征不止性能参数BE5与BE1、BE10相关，并且有性能参数BE9与BE1、BE10相关。

具体实施方式

下面将结合附图和实施例对本发明作进一步的详细说明。本发明通过分析产品输出参数间的相关性来构建耦合模型进行可靠度评估，选取智能电表作为应用对象，对智能电表的输出性能参数进行退化建模，并进行电表的可靠寿命评估。智能电表是典型的具有多性能参数电子产品，能够表征智能电表退化状态的性能参数有累计误差1项，基本误差4项，分别是累计误差CE和基本误差BE1、BE5、BE9、BE10。智能电表的恒定加速退化试验共选取两种加速应力(温度和湿度)进行了三个应力水平的试验，每个应力水平8个样本，具体应力组合见表1。由加速退化试验数据可知智能电表的输出性能参数是具备退化特性的，其退化趋势逐渐上升，根据设计指标有明确的失效阈值，在试验条件下，温度和湿度是促使其发生退化的加速应力。

本发明一种产品故障行为耦合建模和可靠性评估方法，即一种基于Vine-Copula和加速退化试验的产品故障行为耦合建模和可靠性评估方法，见图1所示，其具体实施步骤如下：

步骤一：退化轨迹建模

通过加速退化试验获得智能电表5项关键性能参数在各应力水平下的试验数据。依据智能电表各项性能参数退化轨迹的特点，采用漂移布朗运动对性能参数退化轨迹建模。

1.性能参数的退化轨迹服从模型Δy_t＝μt+σB(t)，其中t为时间，Δy_t为t时刻性能参数的退化量，μ为漂移系数，σ为扩散系数，B(t)为标准布朗运动。

2.建立似然函数其中j表示第j号样本，共n个样本，i表示第i个测试点，共m_j个测试点，t_ji表示第j号样本第i次测试的时间，为所测性能参数的退化量，μ为漂移系数，σ为扩散系数。

3.利用Nelder-Mead单纯形法对似然函数的极大值问题进行求解，得到各应力水平下各性能参数退化轨迹模型的参数估计结果如表2所示。

步骤二：失效机理一致性检验

对于退化轨迹服从漂移布朗运动模型，以智能电表的性能参数CE为例，其失效机理一致性检验可根据

1.对于该参数在每一加速应力下的每一样本，利用Nelder-Mead单纯形法对似然函数的极大值问题进行求解，得到退化模型参数值和其中j表示第j号样本，i表示第i个测试点，共m_j个测试点，t_ji表示第j号样本第i次测试的时间，为所测性能参数的退化量，μ为漂移系数，σ为扩散系数。

2.构建假设检验统计量T服从自由度为n+m-2的t分布。令为三个加速应力下的检验样本，可得三个应力下的检验样本X₁，X₂，X₃，如表3所示。然后逐一对任2个应力下的检验样本X_i、X_j进行T检验。

3.给定显著性水平0.05，查t分布表可知拒绝域为|T|≥t_0.975(14)＝2.1448，令检验样本X_i、X_j分别替换T统计量中的与并带入数据计算，对比t_0.975(14)的值可知均有|T|＜t_0.975(14),即X₁与X₂与X₃之间没有显著差异，该参数在三个应力下的失效机理具有一致性，检验结果见表4。

其他性能参数的失效机理一致性检验可重复步骤1、2和3，直至所有参数通过一致性检验。

步骤三：外推正常应力下性能参数的分布模型

在完成各应力水平下各性能参数退化轨迹建模后，需要将高应力水平下的退化模型参数外推至正常应力下。

1.确定加速因子

根据加速试验条件，选取多应力艾琳加速模型：令为加速应力水平S_h相对于应力水平S_l的加速因子。

2.求解加速模型参数

对性能参数p，在k₁和k₂应力水平下，构造离差平方和函数采用Nelder-Mead单纯形法对离差平方和函数的极小值问题进行求解，可得到对应加速方程中的最优模型参数B、C如表5所示。

3.估计正常应力下退化轨迹模型参数

求得加速模型中的参数之后，使用最小二乘法对正常应力下(温度20℃；相对湿度45％)退化轨迹模型参数进行估计，得到离差平方和函数与采用单纯形法进行优化求解，从而得到正常应力下退化轨迹模型参数μ_p0和σ_p0的点估计，如表6所示。

通过以上步骤，最终得到正常应力下退化轨迹模型为：y_p0(t)＝μ_p0t+σ_p0B(t)。

步骤四：基于Vine-Copula的产品故障行为耦合建模

1.相关性分析

基于各加速应力下相关关系保持不变的假设，可仅选择其中一个加速应力水平下的试验数据进行相关性分析，此处选择第三组应力水平下试验数据。利用相关性度量指标Kendall’sτ系数计算样本关键性能参数之间的相关性见表7，得到结论如下：

1)累计误差CE与基本误差BE之间不具有相关性

2)基本误差BE1、BE5、BE9、BE10存在较强非线性相关性。

2.借助vine图模型将联合分布分解为合适的条件概率相乘的形式，利用copula构建多元相关关系模型。

a.基于D-Vine的建模方法

由分析可知智能电表四项基本误差之间的相关性较为密切，可建立四项基本误差BE之间的D-vine模型，如图4所示。

1)首先，在第一层Vine图模型中，依次对智能电表四项基本误差BE1、BE5、BE9、BE10编码为1、2、3、4，将四项基本误差作为树图中的节点，节点之间按相互关系用短线进行连接，如图2所示。以c_ij表示连接节点i与节点j的copula函数的概率密度，有c_ij＝{c₁₂,c₂₃,c₃₄}

2)Vine图中的第二层树图建立在第一层树图的基础上，以第一层树图中的连接(1,2)、(2,3)、(3,4)作为第二层树图中的节点，用连线进行连接，构建第二层的树图，以图3所示。仍以c_ij表示连接节点i与节点j的copula函数的概率密度，有c_ij＝{c_13|2,c_24|3}

3)Vine图中的第三层树图建立在第二层树图的基础上，以第二层树图中的连接(13|2)、(24|3)作为第三层树图中的节点，用连线进行连接。仍以c_ij表示连接节点i与节点j的copula函数的概率密度，有c_ij＝{c_14|23}

根据D-vine模型可得智能电表四项基本误差可靠度联合分布概率密度函数为：

r(x₁,x₂,x₃,x₄)＝c₁₂·c₂₃·c₃₄·c_13|2·c_24|3·c_14|23·r₁·r₂·r₃·r₄

其中，变量x₁,x₂,x₃,x₄分别代表基本误差BE1、BE5、BE9、BE10，c为对应copula函数的概率密度，r_i表示第i个性能参数的可靠度分布概率密度函数。

b.求解Vine-Copula耦合模型

确定智能电表的可靠度联合分布函数需要首先确定公式r(x₁,x₂,x₃,x₄)中各个Copula函数的形式及参数。本发明中Copula函数备选集为：Gaussian Copula，Frank Copula，Ali-Mikhail-Haq Copula，Clayton Copula。

1)确定Vine模型中第一层树图中的c_ij：c_ij＝{c₁₂,c₂₃,c₃₄}，根据备选的copula函数形式利用Nelder-Mead单纯形法求解似然函数的极大值，得到copula函数的参数估计以及极大似然函数值，然后基于AIC准则选取最为合适的copula函数形式及对应的参数。其中，(k1,k2)＝(1|2,3|2),根据计算结果(见表8)，可以确定c₁₂、c₂₃、c₃₄的最优选择均是Frank Copula。

2)完成Vine图第一层的copula函数的优选后，确定Vine模型中第二层树图中的c_ij:c_ij＝{c_13|2,c_24|3}根据备选的copula函数形式建立似然函数采用Nelder-Mead单纯形法求解似然函数的极大值及其对应的copula函数参数值，然后基于AIC准则选取最为合适的copula函数形式及对应的参数。其中，(p|k,q|k)＝{(1|2,3|2),(2|3,4|3)},经确定c_13|2的最优选择是Frank Copula，c_24|3的最优选择是Clayton Copula。以此类推，对c_14|23进行函数形式选择，可知，c_14|23的最优选择是Frank Copula，至此完成了对式r(x₁,x₂,x₃,x₄)各copula函数形式的优选，得到结果

r(x₁,x₂,x₃,x₄)＝c_Frank(α₁₂,R₁,R₂)·c_Frank(α₂₃,R₂,R₃)·c_Frank(α₃₄,R₃,R₄)

·c_Frank(α_13|2,R_1|2R_3|2)·c_Clayton(α_24|3,R_2|3,R_4|3)

·c_Frank(α_14|23,R_1|23,R_4|23)·r₁·r₂·r₃·r₄

其中，R_1|2，R_2|3，R_1|23可根据多元变量可靠度联合分布的条件概率表达式求得。

3)确定所有的copula函数形式后,对已选定的copula函数的参数一起进行再次估计，建立似然函数L＝r(x₁,x₂,x₃,x₄)，采用了Nelder-Mead单纯形法方法求解极大似然函数，可得到最优参数结果见表9，将所有copula函数的参数回代vine-copula的分解式中，即得到了基于Vine-Copula建立的多元相关关系模型。

步骤五：可靠度求解

1.计算二元变量的可靠度联合分布的条件概率表达式

2.计算多元变量可靠度联合分布的条件概率表达式

3.根据多元可靠度联合分布表达式，可得到四项基本误差耦合的可靠度联合分布为：

R_BEs(t)＝R₁₂₃₄(t₁,t₂,t₃,t₄)

＝R₄(t₄)·R_3|4(t₃|t₄)·R_2|34(t₂|t₃,t₄)·R_1|234(t₁|t₂,t₃,t₄)

其中R_3|4，R_2|34，R_1|234的值为可根据R_hj(x_h|x_j)与R_x|v(x|v)计算。

最终其四项基本误差可靠度联合分布函数图见图5所示。通过分析智能电表加速退化试验数据建模结果可知，当多个性能参数间存在相关性时，若退化建模时不考虑相关性仅以串联模型进行建模，得到的可靠度函数曲线及寿命评估结果会显得保守。相比之下，考虑相关关系的建模方法能在一定程度上给出有充分依据的但不过分激进的评估结果。因此当性能参数间存在相关性时，在退化建模过程中考虑相关关系的作用是有必要的。

针对产品高可靠长寿命特点以及故障机理耦合表征在性能参数相关的问题，本发明研究了基于Vine-Copula和加速退化试验的具有多元变量产品故障行为建模及可靠性评估方法。基于Vine-Copula的建模方法借助Vine-Copula灵活多变的结构，对多种复杂的相关性情况都有各自适用的Vine模型可供用于分析、建立相关性模型，并且无论性能参数退化量之间是线性或非线性关系，都能很好的适用，解决了多元变量可靠性模型中两两变量相关关系表征的问题。

本发明中涉及所有表格如下：

表1各性能参数退化轨迹模型参数估计结果

表2各性能参数加速应力下退化轨迹模型参数估计

表3各产品CE参数估计值及检验样本

表4CE参数一致性检验结果

表5各性能参数加速模型参数估计结果

表6正常应力下各性能参数退化轨迹模型参数

表7性能参数之间相关性计算结果

表8各copula函数形式及参数估计

表9Copula函数优选结果