一种基于自适应遗传算法的立体车库优化方法与流程

本发明涉及立体车库优化方法，尤其是一种立体停车库杆件结构优化方法。

背景技术：

当前城市居民私人车辆急剧增长不仅使得城市道路交通拥堵，而且造成城区停车日益艰难。发展立体式停车场可以有效地缓解城市交通难问题，因为立体车库比较普通平面式停车场有如下好处：1)车辆停车向空间发展，从而节省平面停车场过多占用城市宝贵用地面积；2)可以十分有效地解决城市居住人口密集区停车难的困境。设计经久耐用的立体车库停车设施是重要的，由于立体车库钢结构骨架起着支承停放车辆载荷和分担提升机构载荷的作用，因此车库钢结构骨架进行合理的结构分析和设计对于车库整体承载稳定性起着决定性作用。

技术实现要素：

为了克服已有立体车库的承载稳定性较差的不足，本发明提供一种承载稳定性较好的基于自适应遗传算法的立体车库优化方法。

本发明解决其技术问题所采用的技术方案是：

一种基于自适应遗传算法的立体车库优化方法，包括以下步骤：

1)通过原有设计参量建立立体车库承载有限元模型，计算出每个杆件承载最大弯矩载荷以及最大承载变形数值；

2)构造立体车库钢结构骨架优化设计总重量目标函数，并对所需的设计参量进行当量化；

3)为保证车库结构骨架具有足够的强度、刚度以及稳定性，设定结构应力和节点位移不大于许用值作为约束条件，采用自适应遗传算法，得到立体车库优化方案。

进一步，所述步骤2)中，对部件中的非圆形截面的梁杆部件可以当量成圆形部件来处理，因此当量圆形杆件总重量作为目标函数W， 其其中，f(d)为当量圆形杆件总重量，ρ为材料密度，d_i为当量圆形杆件直径，L_i当量圆形杆件长度，m需要优化的杆件数量。

再进一步，所述步骤3)中，作为优化目标总重量函数的前提条件：承载杆件的最大应力以及最大挠度不大于对应的许用值为约束条件，构造最优化设计的数学模型：

其中，M_max为最大弯矩，y_max为最大中性轴距离，E为材料的弹性模量AC为直梁杆件长度，考虑结构应力耦合效应；CD为横梁承载杆件长度，[y]为最大挠度，[σ]为许用应力。

更进一步，所述步骤3)中，所述自适应遗传算法中，交叉概率和变异概率进行改进：

其中，f_max—群体中量大的适应度，f_avg—每代群体的平均适应度，f′—要交叉的两个个体中较大的适应度；f—要变异个体的适应度值，交叉概率p_c，变异概率p_m，p_c1，p_c2分别为交叉概率的最大值和最小值，p_m1，p_m2分别为变异概率的最大值和最小值，A为自适应遗传算法模型系数；

通过对p_c和p_m进行调整，对于适应度值高于群体平均适应度值的个体，p_c和p_m取较小值，使得该解得以保护进入下一代，而低于平均适应度值的个体，p_c和p_m取较大值，使得该解被淘汰掉。

所述步骤3)中，所述自适应遗传算法的处理过程如下：

3.1)开始

GA＝(MN,f,c,m,pc,pm)，迭代条件为，迭代次数达到MAX次，MN为群体大小，f为个体适应度评价函数，这里为目标函数，c为交叉操作算子，m为变异操作算子，pc为交叉概率，pm为变异概率；

进入遗传算法的遗传优化，依次进行选择、交叉、变异三种遗传方式，并不断循环这个过程直到达到终止条件；

3.2)编码方法

采用二进制编码方法，对待优化的结构设计优化变量进行编码；

3.3)产生初始种群

优化对象d_i的取值范围为[a_i,b_i],利用随机的方法，产生MN个个体的种群，个体t的优化变量为[d₁,d₂,...,d_M,d_M+1,d_M+2,...,d_M+N]；

3.4)个体评价

个体评价函数为修正后的目标函数；

3.5)性能是否满足

判断迭代次数是否满足迭代次数条件；

3.6)最优保存选择操作

按目标函数的值从小到大排序，选取所有种群中MN个个体进行最优保存；

3.7)变异操作和交叉操作。

本发明的技术构思为：立体停车库钢结构承载框架(见附图1)由底部、中部和顶部结构架组成。底部作为车辆进出车库和车辆调头之用，高度最大。中部为标准层，用来停放车辆，它由标准单元组成，可以根据实际车库容量来适当加减层数。顶部用来安装滑轮组并留有检修滑轮组及其他设备的空间，高度最小。钢结构分段制造，用高强度螺栓在现场拼装。

立体车库结构优化设计数学模型：停车库钢结构骨架结构由众多构件组成，为简化计算和减小构件尺寸规格，停车库钢结构可分为梁单元M组，杆单元N组，同一组单元截面积相等。优化设计变量为构件面积，并按型钢规格取离散值。设计变量为X＝[x₁,x₂,...,x_M,x_M+1,x_M+2,...,x_M+N]^T，式中x₁,x₂,...,x_M为第1～M组梁单元的截面积，x_M+1,x_M+2,...,x_M+N为第1～N组杆单元的截面积直径。停车库钢结构骨架的总重量为优化设计的目标函数为

式中ρ_i、A_i(x_i)、L_i第i个单元的密度，截面积和长度，M+N是单元总数。

对部件中的非圆形截面的梁当量成圆形杆件，截面积为目标函数为

式中d_i为当量直径

约束条件：为保证停车库钢结构骨架具有足够的强度、刚度和稳定性，以结构应力和节点位移不大于许用值作为减轻结构总重量设计的约束条件， 即

式中σ_max(d_i)，U_max(d_i)表示为结构中的最大应力和最大节点位移。为许用节点应力和许用节点位移。

约束条件为：

a)弯曲强度：最大弯矩约为M_max，通过建立承载有限元模型计算出，弯曲强度校核公式为y_max为求应力的点离中性轴的最大距离。I_z则是横截面对于中性轴z的惯性矩，式中

弯曲强度所决定的约束条件为：

b)根据刚度要求，最大挠度[y]≤4.0mm，即材料的拉伸压缩弹性模量E。

刚度所决定的约束条件为：

构造最优化设计的数学模型：采用罚函数法来处理不等式约束问题，即计算出由于违背约束条件而产生的罚函数c，并用它修正目标函数。具体的做法：若不满足上述不等式，即g_j(d_i)＞0,c_j＝g_j(d_i)；反之若满足上式，c_j＝0。于是罚函数汇总为

修正后的目标函数为

f(d_i)＝F(d_i)(1+kc) (4)

其中系数k是一常数，它的取值应视约束条件的重要性而定。

本发明的有益效果主要表现在：承载稳定性较好。

附图说明

图1是立体车库钢结构示意图，其中，(a)是正视图，(b)是侧视图。

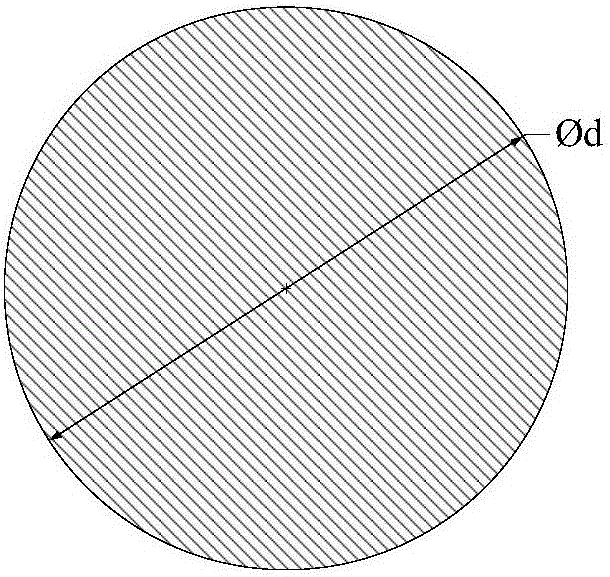
图2是杆件当量直径示意图。

图3是自适应遗传算法的流程图。

图4是现有遗传算法和改进遗传算法计算结果比较图。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1～图4，一种基于自适应遗传算法的立体车库优化方法，包括以下步骤：

1)通过原有设计参量建立立体车库承载有限元模型，计算出每个杆件承载最大弯矩载荷以及最大承载变形数值；

2)构造立体车库钢结构骨架优化设计总重量目标函数，并对所需的设计参量进行当量化；

3)为保证车库结构骨架具有足够的强度、刚度以及稳定性，设定结构应力和节点位移不大于许用值作为约束条件，采用自适应遗传算法，得到立体车库优化方案。

进一步，所述步骤2)中，对部件中的非圆形截面的梁杆部件可以当量成圆形部件来处理，因此当量圆形杆件总重量作为目标函数W， 其中，f(d)为当量圆形杆件总重量，ρ为材料密度，d_i为当量圆形杆件直径，L_i当量圆形杆件长度，m需要优化的杆件数量。

再进一步，所述步骤3)中，作为优化目标总重量函数的前提条件：承载杆件的最大应力以及最大挠度不大于对应的许用值为约束条件，构造最优化设计的 数学模型：

其中，M_max为最大弯矩，y_max为最大中性轴距离，E为材料的弹性模量AC为直梁杆件长度，考虑结构应力耦合效应；CD为横梁承载杆件长度，[y]为最大挠度，[σ]为许用应力。

更进一步，所述步骤3)中，所述自适应遗传算法中，交叉概率和变异概率进行改进：

其中，f_max—群体中量大的适应度，f_avg—每代群体的平均适应度，f′—要交叉的两个个体中较大的适应度；f—要变异个体的适应度值，交叉概率p_c，变异概率p_m，p_c1，p_c2分别为交叉概率的最大值和最小值，p_m1，p_m2分别为变异概率的最大值和最小值，A为自适应遗传算法模型系数；

通过对p_c和p_m进行调整，对于适应度值高于群体平均适应度值的个体，p_c和p_m取较小值，使得该解得以保护进入下一代，而低于平均适应度值的个体，p_c和 p_m取较大值，使得该解被淘汰掉。

所述步骤3)中，所述自适应遗传算法的处理过程如下：

3.1)开始

GA＝(MN,f,c,m,pc,pm)，迭代条件为，迭代次数达到MAX次，MN为群体大小，f为个体适应度评价函数，这里为目标函数，c为交叉操作算子，m为变异操作算子，pc为交叉概率，pm为变异概率；

进入遗传算法的遗传优化，依次进行选择、交叉、变异三种遗传方式，并不断循环这个过程直到达到终止条件；

3.2)编码方法

采用二进制编码方法，对待优化的结构设计优化变量进行编码；

3.3)产生初始种群

优化对象d_i的取值范围为[a_i,b_i],利用随机的方法，产生MN个个体的种群，个体t的优化变量为[d₁,d₂,...,d_M,d_M+1,d_M+2,...,d_M+N]；

3.4)个体评价

个体评价函数为修正后的目标函数；

3.5)性能是否满足

判断迭代次数是否满足迭代次数条件；

3.6)最优保存选择操作

按目标函数的值从小到大排序，选取所有种群中MN个个体进行最优保存；

3.7)变异操作和交叉操作。

实例：结构分为7组单元为例说明，梁单元M＝5组，杆单元N＝2组，待优化的参量为[d₁,d₂,...,d₇]。所选用钢材料密度ρ＝7850kg/m³。应力强度小于等于100MPa以及许用挠度小于等于4mm。运用MATLAB遗传算法工具箱进行求解， 种群规模为30，进化代数为100，初始交叉率P_c1＝0.6，P_c2＝0.3；初始变异率P_m1＝0.05，P_m2＝0.001。

设定立体车库模型基本参数：底部为2.6m；中部为2.2m；顶部高度为1.5m。车库设计容量为20辆，需要10层停车标准单元，这样车库总层数为12层，总高度为H＝2.6+10×2.2+1.5＝26.1m。采用三维梁单元和杆单元模拟实际结构建立有限元模型，用固定约束边界条件模拟结构在基础上的安装情况。梁单元具有拉伸、压缩、扭转和弯曲能力，每个节点有6个自由度，截面形状尽量选取市场上有售的型材。杆单元为单向拉压单元，每个节点有3个移动自由度。整个车库钢结构骨架共有330个单元，172个节点。除考虑停车库钢结构骨架自重和机械传动系统的重量外，还考虑每个车位均受额定车辆载荷的作用情况。这里的停车库共有20个车位，额定车辆载荷为1600kg。钢结构骨架的受力情况主要包括：钢结构本身自重，结构架上各停车位的车辆及固定叉梳重量，提升系统制动所产生的惯性力，驱动装置的重力，顶部梁架所受滑轮组和配重的重力，整体结构所受的风力、地震载荷以及由于外界环境温度变化而引起的温度应力等，它们以集中或均布方式作用。按基本载荷作用情况，将停车库钢结构骨架结构分析的计算工况分为。如表1所示的4种工况：

表1

结果分析以及结论：优化设计与原设计方案结果比较见表2。表中d₁～d₇分别为角柱、前后侧中间立柱、左右横柱、前后横柱、上下支承柱、左右腹杆、前后腹杆的当量直径。从表1可以看出，传统自适应遗传算法得到的优化设计方案较原方案有很大改进，可使结构重量降低30％左右。经过改进的自适应遗传算法可以使结构重量降低41％。由此可见，采用新的自适应遗传算法建立钢结构骨架优化设计模型，对钢结构骨架进行优化设计，可进一步降低材料的消耗，从而提高车库制造成本的经济性。

表2

交叉概率和变异概率进行改进的思路：遗传算法的参数中交叉概率p_c和变异概率p_m的选择是影响遗传算法行为和性能的关键所在，直接影响算法的收敛性，p_c越大，新个体产生的速度就越快。然而过大时遗传模式被破坏的可能性也越大，使得具有高适应度的个体结构很快就会被破坏；但是如果p_c过小，就不易产生新的个体结构；如果p_m过小，就不易产生新的个体结构；如果p_m取值过大，那么遗传算法就变成了纯粹的随机搜索算法。针对不同的优化问题，需要反复实验来确定p_c和p_m，本专利针对立体车库结构采用一种自适应遗传算子，使p_c和p_m能够随适应度自动改变。当种群各个体适应度趋于一致或者趋于局部最优时，使p_c和p_m增加，而当群体适应度比较分散时，使p_c和p_m减少。同时对于适应值高于群体平均适应值的个体，对应于较低的p_c和p_m，使该解得以保护进入下一代，而低于平均适应值的个体，结合个体违反约束的情况给予相对较高的p_c和p_m，使该解得以保护进入下一代；而低于平均适应值的个体，结合个体违反约束的情 况给予相对较高的p_c和p_m，使该解得以保护进入下一代；而低于平均适应值的个体，结合个体违反约束的情况给予相对较高的p_c和p_m，使该解被淘汰掉。因此，自适应的p_c和p_m能够提供相对某个解的最佳p_c和p_m。通过自适应遗传算子使算法在保持群体多样性的同时，保证遗传算法的收敛性。通过对最优保护遗传算法中的p_c和p_m按照上述思想进行改进，使得算法中的p_c和p_m按如下公式进行自适应调整，得到传统自适应算法：

式中f_max—群体中量大的适应度；f_avg—每代群体的平均适应度；f′—要交叉的两个个体中较大的适应度；f—要变异个体的适应度值。当适应度值低于平均适应度值时，说明该个体是性能不好的个体，对它就采用较大的交叉率和变异率；如果适应度值高于平均适应度值，说明该个体性能优良，对它就根据其适应度值取相应的交叉率和变异率。可以看出，当适应度值越接近最大适应度时，交叉率和变异率就越小；当等于最大适应度值时，交叉率和变异率的值为零。这种调整方法对于群体处于后期比较合适，但对于进化初期不利，因为进化初期群体中的个体几乎处于一种不发生变化的状态，而此时的优良个体不一定是优化的全局最优解，这容易使进化走向局部最优解得可能性增加。为此，可以进一步的改进，使群体中最大适应度值的个体的交叉率和变异率不为零，分别提高到p_c2和p_m2这就相应地提高了群体中表现优良的个体的交叉率和变异率，使得它们不会处于一种近似停滞不前的状态。为了保证每一代的优良个体不被破坏，采用最优保护策略，使它们复制到下一代中。经过上述改进，p_c和p_m计算表达式如下：

p_c＝p_c1(1+kc) f'＜f_arg (7)

p_m＝p_m1(1+kc) f＜f_arg

式中：p_c1，p_c2分别为交叉概率的最大值和最小值，p_m1，p_m2分别为变异概率的最大值和最小值。这个算法采用精英策略起着保护和推广个体的作用，但是当个体数目过大的时，会使较差的个体变异能力下降，导致种群进化陷入停滞不前，造成局部收敛。容易产生局部最优解。为了克服以上两种遗传算法的不足，本专利自适应遗传算法的交叉概率和变异概率进行改进：

这样，通过对p_c和p_m进行调整，对于适应度值高于群体平均适应度值的个体，p_c和p_m取较小值，使得该解得以保护进入下一代，而低于平均适应度值的个体，p_c和p_m取较大值，使得该解被淘汰掉。故这种方法可提供某个解相对较佳的p_c和p_m，在保持群体多样性的同时，保证GA的多样性。