一种SVR非线性系统建模参数优化方法与流程

本发明涉及一种SVR非线性系统建模参数优化方法。

背景技术：

支持向量回机(SVR)通过引入核函数，将低维空间的原始问题化为高维核空间的线性问题进行求解。对于训练样本数量有限情况下的非线性系统建模问题，SVR根据结构风险最小化原则，在训练样本数据逼近程度与模型的泛化能力两者间取得平衡。与基于经验风险最小化的算法，如神经网络、最小二乘法，支持向量回归建模避免了对样本数量和样本质量的依赖，也不会陷入局部极小问题。

SVR建模的泛化能力取决于模型参数的选取。对于模型参数的选择常用的方法有交叉验证法，genetic algorithm(GA)参数优化算法、particle swarm optimization approach(PSO)参数优化算法等。交叉验证法的基本思想是把原始数据进行分组，一部分作为训练集，另一部分作为验证集，首先用训练集对SVR进行训练，再利用验证集来测试训练得到的模型，以此作为评价SVR的性能指标。GA优化算法首先选择可能的模型参数作为初始种群，然后通过多次组合交叉和变异操作，根据模型训练效果，寻找最好的模型参数。PSO同遗传算法类似，是一种基于迭代的优化工具。将模型参数看作是解空间中的粒子，通过迭代操作，粒子在解空间追随训练效果最优的粒子进行搜索，最终得到最优模型参数。从某种意义上来讲，这些方法属于试凑法，完全忽略了核空间的特性，参数搜索区间大，训练时间长。

技术实现要素：

本发明解决的技术问题：如何提供一种SVR非线性系统建模参数优化方法，以克服现有技术的参数搜索区间大、训练时间长的问题。

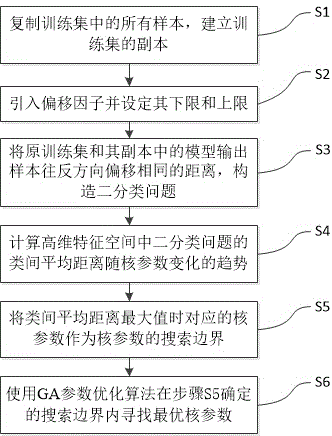
为解决所述的技术问题，本发明提供了一种SVR非线性系统建模参数优化方法，包括以下步骤：

S1：复制训练集中的所有样本，建立训练集的副本；

S2：引入偏移因子并设定其下限和上限；

S3：将原训练集和其副本中的模型输出样本往反方向偏移相同的距离，构造二分类问题；

S4：计算高维特征空间中二分类问题的类间平均距离随核参数变化的趋势；

S5：将类间平均距离最大值时对应的核参数作为核参数的搜索边界；

S6：使用GA参数优化算法在步骤S5确定的搜索边界内寻找最优核参数。

优选地，步骤S1所述的训练集T＝{(x_i,y_i),i＝1,...l}，x_i∈Rⁿ是对系统的输入，y_i∈R为系统的输出。

优选地，步骤S2所述的偏移因子τ的上限τ_max和下限τ_min的计算公式为τ_min＝q₁G，τ_max＝q₂G，其中q₁，q₂为位移系数，G为y_i的极差。

优选地，步骤S3所述的构造二分类问题为区分D+和D-两类的二分类问题，公式如下：

其中，i＝1,2,…,l。取τ＝τ_min和τ＝τ_max，分别构造二分类问题。

优选地，步骤S4所述的核参数为高斯核函数K(x_i,x)＝exp(-γ||x_i-x||²)的宽度参数γ。

优选地，步骤S4所述的类间平均距离计算公式为：

本发明提供的一种SVR非线性系统建模参数优化方法有如下优点：1)充分利用了核空间的特性，确定了核参数的搜索范围，解决了需设定足够大搜索范围的问题，避免了局部最优的问题。2)在缩小了的搜索范围内使用GA算法进行核参数的优化，提高了SVR训练的效率，解决了SVR训练时间长的问题。

附图说明

图1为本发明所提供的方法流程图。

图2为本发明中的类间平均距离随核参数变化的趋势曲线。

图3为本发明中的SVR建模效果。

具体实施方式

下面结合说明书附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例仅用于说明本发明，但不用来限制本发明的范围。

实施例一：

如图1所示，本实施例记载了一种SVR非线性系统建模参数优化方法，包括以下步骤：

S1：复制训练集中的所有样本，建立训练集的副本；

S2：引入偏移因子并设定其下限和上限；

S3：将原训练集和其副本中的模型输出样本往反方向偏移相同的距离，构造二分类问题；

S4：计算高维特征空间中二分类问题的类间平均距离随核参数变化的趋势；

S5：将类间平均距离最大值时对应的核参数作为核参数的搜索边界；

S6：使用GA参数优化算法在步骤S5确定的搜索边界内寻找最优核参数。

实施例二：

本实施例记载了一种SVR非线性系统建模参数优化方法，其具体步骤如下：

1、使用0.01Hz的单正弦信号x(t)＝sin(0.02πt)在100秒的时间范围内，对系统y(t)＝sin²(x(t))+cos³(x(t))+σ进行激励，其中σ是均值为0的高斯白噪声信号，以获取训练集T＝{(x_i,y_i),i＝1,...100}。复制训练集中的所有样本，建立训练集的副本。

2、引入偏移因子τ并设定其下限τ_min＝q₁G和上限τ_max＝q₂G，其中q₁，q₂为位移系数，G为y_i的极差。取位移系数q₁＝0.2，q₂＝8，计算y_i的极差G＝0.1787，得τ_min＝0.0357，τ_max＝1.4296。

3、将原训练集和其副本中的模型输出样本往反方向偏移相同的距离，构造D+与D-两类数据集的二分类问题，当τ＝τ_min时，构造的二分类问题为：

当τ＝τ_max时，构造的二分类问题为

4、分别计算τ＝τ_min和τ＝τ_max时高维特征空间中二分类问题的类间平均距离随核参数变化的趋势。

所述的核参数为高斯核函数K(x_i,x)＝exp(-γ||x_i-x||²)的宽度参数γ。所述的类间平均距离计算公式为：

所述的类间平均距离随核参数变化的趋势曲线如图2所示。

5、将类间平均距离最大值时对应的核参数作为核参数的搜索边界，确定其搜索范围为[2^-2,2⁸]。

6、使用GA参数优化算法在步骤5获得的搜索范围内寻找最优核参数，得到最优核参数γ＝0.9710，应用该核参数的SVR建模效果如图3所示。