一种高压断路器零件的可靠性分析及优化方法与流程

本发明涉及到机械零件可靠性分析技术，具体地说，是一种高压断路器机械零件的可靠性分析及优化方法。

背景技术：

随着社会经济的快速发展和电力需求的不断增长，多个国家都提出了高效、可靠的智能电网建设规划，智能电网对电力设备安全稳定运行的能力提出了更高要求，其中电力设备的可靠性处于至关重要的地位。高压断路器是电力系统中重要的控制和保护设备，若其产生故障，将对电力系统的安全稳定运行产生重要影响。高压断路器故障可分为机械和电气两大类，国际大电网会议对多个国家断路器故障的统计数据表明，高压断路器使用过程中最为多发的是操动机构的机械故障。从我国电网中断路器故障的统计数据来看，机械故障更是占有较高的比例。高压断路器操动机构具有复杂的机械结构，结构中某个零件的失效必然造成开合过程达不到规定要求，引起断路器故障，对电网可靠性产生影响。可靠性是指机械产品在规定的条件下和规定的时间内完成规定功能的能力，是衡量机械产品质量的一个重要指标。机械可靠性分析是将概率统计理论、失效物理和机械学等结合起来的综合性工程技术，机械可靠性分析将机械零件的各种变量，如材料强度、疲劳寿命、载荷、几何尺寸及应力等所具有的多值现象都看成是服从某种分布的随机变量，用概率统计方法评估机械零件稳定工作的能力，同时为机械零件的优化设计提供参考。舒服华(舒服华，高压断路器弹簧操动机构合闸弹簧可靠性分析，高压电器，2007，43(5)：368-370，373)针对高压断路器弹簧操动机构合闸弹簧失效问题，运用可靠性设计原理，根据解析方法分析了合闸弹簧的可靠性并提出了优化方法。石飞等(石飞，林莘，徐建源等，真空断路器中关键零件机械可靠性计算与分析，高压电器，2005，41(1)：32-35)给出了两种与高压断路器机械可靠性特点相适应的机械可靠性计算模型，并运用模型对目前在我国中压电网中应用十分广泛的真空断路器的机械可靠性进行了计算与分析，得到了对断路器机械可靠性影响较大的主要机械零部件的设计可靠度和在断路器不同开断次数下的可靠度。两种方法都在断路器零件可靠性分析状态函数具有解析式的情况下进行分析，对于分析零件结构复杂，状态函数难以用解析式表达的情况，这种分析方法存在其局限性。

技术实现要素：

本发明的目的在于提供一种高压断路器零件的可靠性分析及优化方法，解决难以得到零件状态函数解析式的可靠性分析问题，同时根据灵敏度分析结果，对零件进行优化设计。

本发明采用的技术方案为：一种高压断路器零件的可靠性分析及优化方法，包括以下步骤：

一、根据实际使用情况，选择断路器中易于发生故障的机械零件，根据其常见的故障类型和失效模式确定可靠性分析的随机变量x₁,x₂,……,x_n，根据随机变量的类型，确定各个随机变量的概率密度函数f(x_i)。

二、根据随机变量及机械零件失效模式建立可靠度分析的状态函数，该状态函数可定义为R(x₁,x₂,……,x_n)，状态函数种包括有限元分析的响应量y(x₁,x₂,……,x_m)。

三、建立机械零件的参数化有限元分析模型，以获得状态函数中的有限元响应量y(x₁,x₂,……,x_m)。

四、结合建立的参数化有限元分析模型，利用蒙特卡洛方法分析机械零件可靠度和随机变量灵敏度。

五、根据可靠度和灵敏度分析结果，优化机械零件设计，提高高压断路器的可靠性和经济性。

作为优选，所述步骤一中的随机变量x₁,x₂,…….,x_n为载荷、强度、几何尺寸、材料参数等与结构、材料属性有关的随机变量。

机械零件载荷的概率分布根据载荷类型，通过实验测定或统计数据确定；机械零件强度的随机变量根据材料类型，查询相关数据资料获得；认为几何尺寸的随机变量符合正态分布，标准差按“3σ”原则确定；材料参数包括泊松比、弹性模量等，根据材料相关数据确定。

作为优选，所述步骤二中可靠度分析的状态函数R(x₁,x₂,……,x_n)中包括通过对参数化有限元模型求解获得的应力响应量y(x₁,x₂,……,x_m)，有限元模型中的应力响应量y(x₁,x₂,……,x_m)中的随机变量x₁，x₂，……x_m可以为断路器零件的几何尺寸、材料参数等。零件的有限元分析模型采用参数化建模，直接修改参数化有限元文件中对应参数实现蒙特卡洛模拟。

作为优选，所述步骤四中所述的蒙特卡洛方法用于零件可靠度和灵敏度计算，具体的蒙特卡洛方法实现方式为：利用计算机产生一组符合随机变量分布规律的随机数，使随机数均匀分布于样本空间，每产生一个随机数相当于对随机变量进行一次抽样。根据当前抽样产生的随机数组，改变零件参数化有限元模型中对应的参数值，调用有限元求解器进行有限元分析，根据有限元分析结果，获取当前抽样的最大应力响应量，当此应力大于零件强度时，零件失效，反之，零件安全。设总的蒙特卡洛模拟次数为N，安全的次数为Ns，则零件的可靠度近似值为R＝Ns/N。

作为优选，所述步骤五中由零件类型，确定优化目标，根据灵敏度分析结果，将变量对可靠性结果的影响程度排序，优化零件参数，重新计算零件的可靠度。

有益效果：本发明采用采用蒙特卡洛法结合高压断路器零件的有限元分析结果，分析高压断路器零件的可靠性，有效解决传统分析计算中对于复杂机械零件难以求得可靠度函数解析式，无法进行可靠度分析的情况。同时，根据可靠性分析提供的灵敏度分析结果，对零件的参数进行优化，可提高高压断路器机械零件的可靠度。

附图说明

图1为可靠性分析及优化方法的流程图

图2为某断路器传动机构简图。

图3为网格划分后的的零件有限元模型。

图4为零件静力分析获得的应力云图结果。

图5为蒙特卡洛方法的流程图。

图6为灵敏度分析的结果。

具体实施方式

下面结合附图和具体实施方式对本发明做进一步说明。

下述实施例中所涉及到的高压断路器零件是其操动机构中的拐臂零件：

图1为可靠性分析及优化方法的流程图，主要分为确定可靠性分析的随机变量和其概率密度函数、建立可靠度分析的状态函数和有限元分析响应量、建立机械零件的参数化有限元分析模型、利用蒙特卡洛方法分析机械零件可靠度和随机变量灵敏度、优化机械零件设计。

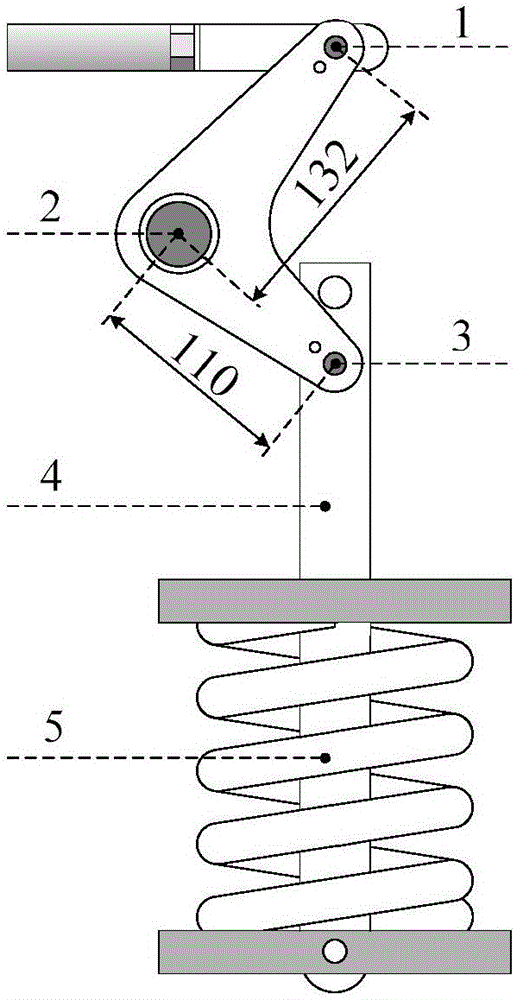
图2为某断路器传动机构简图，其中有：1、上轴孔，2、转轴，3、下轴孔，4、拉杆，5、弹簧。待分析零件为固定于轴孔上的拐臂零件。该拐臂连接断路器分闸弹簧拉杆和灭弧室绝缘连杆，传递分合闸过程中弹簧释能所产生的分合闸力，是分合闸力传递过程中的重要一环。待分析拐臂的材料为45号钢，其屈服强度σ_s＝408MPa，抗拉强度σ_b＝676MPa，弹性模量E＝206000MPa，泊松比v＝0.285。

建立分析零件可靠度的状态函数，根据零件特点，选取的随机变量为σ_s、F、E、v、r，分别为材料的屈服强度、弹簧的最大负荷、材料的弹性模量、材料的泊松比和拐臂销孔的半径。假设变量均服从正态分布，E、v通过查询相关材料的数据可得，F的标准差根据S_F＝0.2F/3确定，半径r的标准差按“3σ”原则取，根据各随机变量，建立的可靠度的状态函数为R＝σ_s-ansys(F,E,v,r)。

图3为网格划分后的的零件有限元模型。基于商业化有限元软件ANSYS采用APDL语言进行机械零件参数化建模，建立其有限元分析模型，根据拐臂零件的特点，选用SOLID45单元，对拐臂进行自动网格剖分。

图4为零件静力分析获得的应力云图结果。分析中考虑此拐臂因故障卡滞，同时受到分闸弹簧给出的分闸力，在模型轴孔面上施加X、Y、Z方向的位移约束，约束拐臂的转动，同时根据分闸弹簧最大负荷，在销轴孔上施加相应的载荷，对拐臂模型进行静力分析。

蒙特卡洛法又称为随机模拟法或统计抽样法，从已知的模型输入的概率分布随机抽样构造随机变量，然后根据随机变量计算结果输出的不确定因素，得到响应量的数字特征。利用蒙特卡洛法分析可靠性问题，关键是要产生服从随机变量分布的随机数，乘同余法是广泛采用的随机数产生方法。乘同余法的递推公式为：

x_i+1＝ax_i(modm),i＝0,1,2,…,n

式中：模数m、乘数a及初值x₀均为正整数，且有m>0，m>a，m>x₀。

图5为蒙特卡洛方法的流程图。根据蒙特卡洛法，产生当前第i次采样的可靠度计算模型中随机变量σ_s、F、E、v、r的随机数组A_i，修改ANSYS拐臂分析的APDL文件中对应的参数，调用ANSYS求解器求解，根据有限元分析结果，获得当前采样的零件最大主应力σ，判断最大主应力σ是否大于当前强度采样的随机数σ_si，当应力大于强度时，零件失效，反之，零件安全。重复此蒙特卡洛抽样与ANSYS分析的过程，当抽样次数达到所设定的蒙特卡洛模拟次数N时，若安全的次数为Ns，则零件的可靠度近似值为R＝Ns/N，同时，根据可靠度分析过程中产生的灵敏度结果，对灵敏度结果进行排序，最后获得拐臂零件可靠度与灵敏度分析结果。

图6为拐臂零件的灵敏度分析结果，根据柱状图可以看到：材料的泊松比v和弹性模量E对拐臂可靠度的影响较小，载荷和强度对拐臂的可靠性有较大的影响，同时，销孔半径也是可靠度的主要影响因素之一。在零件的优化过程中，为提高拐臂相应的可靠度，可优化销孔半径，减小公差。将优化后的零件再进行一次可靠性分析，验证根据灵敏度优化的效果。

应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。