一种数据分析中获取因变量与自变量回归关系的方法与流程

本发明涉及数据分析处理技术领域，尤其是一种一种数据分析中获取因变量与自变量回归关系的方法。

背景技术：

数据分析的过程，回归分析是经常使用的一种方法。传统的回归过程，需要用户按相关的某个模型的关系，选取自变量与因变量，通过手工的方法进行数据的输入并逐个分析最终的结果，再对得出的结果进行检查回归系数、自变量与实际因变量的准确率。对于无法很明确地查看出多个自变量与因变量的关系时，需由用户自行逐个过程进行操作。整个过程费时费力效率低，而且输入的数据量，对于全部数据来说因变量与自变量又有可能有不同的因果关系，直接使用传统的方法无法进行数据区域的区别分析，比较难达到准确的分析效率。

技术实现要素：

本发明解决的技术问题在于提供一种数据分析中获取因变量与自变量回归关系的方法；可以高效地获取输入的因变量与自变量的最优对应关系，用于以后的数据预测。

本发明解决上述技术问题的技术方案是：

所述的方法包括以下几个步骤：

步骤1：对用户输入的因变量与自变量，进行数据标准化处理，并保存该结果备用；

步骤2：对数据进行回归分析，分析出类似的数据特征，从类似的数据特征中进行纵向的自变量选取，通过调用相关的线性分析算法，得出因果关系；

步骤3：对比计算分析出来的结果与实际的结果，获得自变量与因变量的最优关系，将最终的最优结果展示给用户用于最终的选择。

所述数据标准化具体步骤为：

步骤一、获取因变量及各自变量，分别求各自因变量、自变量的平均值，作为基准数据β；

步骤二、分别求各自因变量的标准差α，作为扩大系数，扩大系数通过标准差的方式求出，公式为：

公式中数值x₁，x₂，x₃，......x_N是各自变量的值，其中μ为各自变量的算术平均值；

步骤三、对因变量及各自变量，分别通过公式Z′＝αZ+β求出标准化后的值，Z′为标准数据，β为基准数据，α是扩大系数。

所述数据回归分析具体步骤为：

步骤一、对输入的自变量数据按不同聚类数量，多次进行聚类分析，得出多个按不同聚类数量的分析结果；

步骤二、对某一特定聚类数量的分析结果，按不同的类别，从中选取自变量，分析选取的自变量与因变量的关系，得出回归系数；再通过回测的方法，计算出准确率，选取准确率最高的自变量与因变量的回归关系；对不同的数据类别采用相同的方法获取准确率最高的回归关系；

步骤三、对分类出来的不同的类别的回归关系进行分析，合并自变量一样、回归系数相差不大的类别，形成统一的回归关系；自变量不同或回归系数相差太大的，形成各数据区域独立的回归关系；

步骤四、重复步骤二、步骤三，对不同数据聚类数量的回归关系进行分析，得出各聚类数据下的最优回归关系和回归系数。

所述的聚类分析可采用K-Means聚类算法，计算聚类的距离可使用欧氏距离计算方法，计算公式如下：

欧氏距离d_ij表示两个n维向量a(x11，x12，...，x1n)与b(x21，x22，...，x2n)间的距离。

所述的回归关系可采用最小二乘法多项式曲线拟合，拟合的过程可通过自实现的方式进行，或是通过调用相关通用的拟合工具，直接获取拟合结果，拟合公式为：

假设给定数据点(x_i，y_i)(其中i＝0，1，2，…，m)，为所有次数不超过n(n≤m)的多项式构成的函数类，现求使得满足min公式的P_n(x_i)称为最小二乘拟合多项式，通过代入相关的(x_i，y_i)值并假设min为最小0，可得出n条关于a₀，a₁，a₂，…，a_n的多项式，求解出以上的a₀，a₁，a₂，…，a_n的多元函数，得出a₀，a₁，a₂，…，a_n的具体的值。

所述获取自变量与因变量的最优关系具体步骤为：

步骤一、对各不同的聚类数量分析出来的最优回归关系、回归系数，分析得出最优的准确率，或是最优的前几个的准确率；把分析结果展示给用户，为用户的最终选择提供数据依据；

步骤二、对用户选择的最优结果，提供自变量与因变量的标准化转换公式，各聚类的中心及分析的回归自变量、回归系数，用于最终的数据预测；

步骤三、用户通过提供的自变量与因变量的标准化转换公式，各聚类的中心及分析的回归自变量、回归系数；在输入新的预测数据时，先进行自变量的标准化，再与各聚类中心进行对比，选取距离最近的数据区域，应用该区域的自变量及回归系数，从而预测出标准化的预测值；再通过标准化公式反推预测的原始值。

本发明的有益效果是：

本发明方法是通过利用计算机可不断计算、并且可进行预测结果的回测的优势，通过对数据的标准化，提高数据的准确性，按聚类的方式使数据在横向上进行区域回归区分，再从自动选取自变量上进行纵向的计算，从而得出数据分析的最优回归结果，并形成数据分析预测的最终结果，用于最后的数据预测。在此方法中为用户快速直接分析出最优的因果关系，极大提高获取因变量与自变量回归关系的效率，形成一种高效获取多个自变量与因变量的关系的最优方法；从而提高数据回归分析过程中对因变量与多个自变量的主要成份的分析，简化了数据回归分析的过程，提高了因变量与自变量获取的效率。

附图说明

下面结合附图对本发明进一步说明：

附图1是本发明获取最优因变量与自变量关系流程图。

具体实施方式

本发明通过分析用户输入的因变量与多个自变量，对数据进行标准化处理，同时保存各因变量与自变量的数据标准化结果用于后续的数据预测；后先对数据从横向的角度进行分类，从而分析出类似的数据特征，再从类似的数据特征中进行纵向的自变量选取，通过调用相关的线性分析算法，得出因果关系，通过计算分析出来的结果与实际的结果进行对比，分析出某些自变量与因变量的最优关系，把最终的最优结果展示给用户用于最终的选择，使用此方法可为用户从多个自变量中高效获取与因变量的最优因果关系，可极大提高获取因变量与自变量回归关系的效率，作为优化数据分析过程获取主要因果成份关系的一种方法。

对输入的因变量及多个自变量，需进行各输入数据的数据标准化处理，就是将输入的所有变量包括因变量都先转化为标准数据，再进行线性回归分析，使标准化后的数据此时得到的回归系数更能反映对应自变量的重要程度；数据标准化可采用如下转换通式：Z′＝αZ+β，式中，Z′为标准数据，β为基准数据，一般等于原始数据的平均值X_bar，α是扩大系数，一般等于原始数据的标准差S。

在因变量与自变量都进行了数据标准化后的基础上，按各自变量的数据进行多类别的聚类分析，聚类分析的目的，是为了发现不同数据在各个类别上的特征，从而可以从特征明显的数据上，获取明确的回归系数关系；如果进行分类后得出的回归系数关系相差不大，那可看作分析的结果数据是一致的，可作为统一的回归因果关系；对于进行分类后的回归系统相关比较大，则说明不同的类别数据在各区域上有不同的回归因果关系，在后续使用回归结果时可从计算出来的各聚类中心进行比对，选取与各聚类中心最近的回归因果关系进行数据的预测。

在对自变量进行某个类别的聚类分析后，按分析的结果，循环在种个分类类别上选取某几类自变量与因变量形成回归关系，得出回归系数，再把特定类别的自变量数据用于回归测试，计算出准确率，这样从多个自变量中，选取出最优的自变量与因变量的因果关系、回归系数；不同的类别使用这种方法，从而使所有类别的数据都形成一定的回归关系。

在使所有类别的数据都形成了最优回归关系后，分析各类别所选取的自变量及各自变量的回归系数，如果所选取的自变量是一样的，及各自变量的回归系统相关不大的，则可把回归系数进行合并，从而形成统一的回归关系，也说明数据符合统一的回归关系，回归过程选择出了最优的自变量与因变量的最优关系；如果各分类类别所选取的最优回归自变量与各自变量的回归系数是不一样的或相差很大，则说明输入的自变量与因变量的回归关系在各个区域是不同的，需使用不同的回归关系，则需保存各类别的数据中心点及各类别的回归自变量及系统，用于后续对各区域的回归关系的计算。

对输入的多个自变量的数据的聚类、选取自变量与因变量的回归分析，可通过程序的方式调用R语言或自实现程序进行实现，通过调用已实现的方法以提高进行自变量与因变量关系进行选择分析的效率。

对于输入的数据量比较多的情况，需对数据进行更多类别的分类，从而区分出各个区域数据的特征，更加详细地对各个区域的自变量与因变量的最优因果关系的回归分析，得出回归系数，而最重要的是在得出各区域的回归关系回归系数后，需对回归结果进行归纳总结，全部统一的回归关系，从而优化最终的回归关系的计算。

通过多次按不同的聚类数量进行横向、纵向的数据计算，最终得出各聚类数量下的最优回归关系及回归系数，对比各聚类数量的最优结果，最终给用户最优的聚类分类下的各区域的中心数据、回归自变量、回归系数，显示最优的因变量与自变量的关系。

在得出最优的聚类分类下的各区域的中心数据、回归自变量、回归系数，结合各自变量的标准化指标，输入新的预测数据，首先通过与各类别的中心数据进行对比选取距离最近的区域，套用距离最近的回归变量及回归系统，从而得出最终的预测结果。

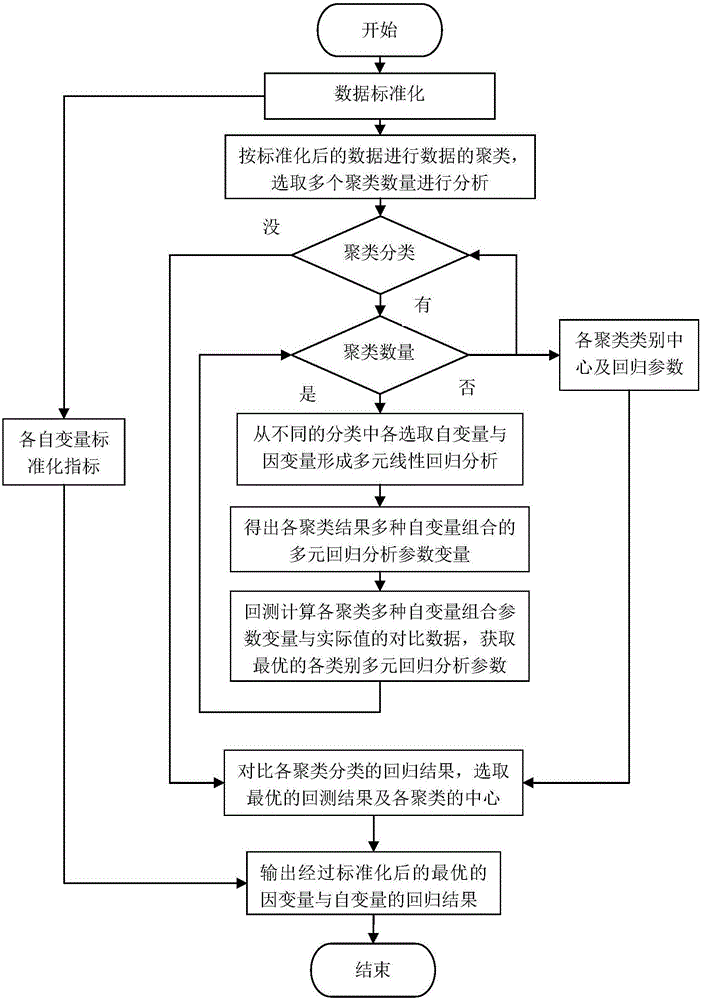
按照流程而言，如图1所示，本发明的实现主要包括三部分，数据标准化、数据横向纵向回归分析、获取最优对应关系，三部分的具体步骤如下：

一、数据标准化：

步骤一、分别获取因变量及各自变量，分别求各自因变量、自变量的平均值X_bar，作为基准数据β；

步骤二、分别求各自因变量的标准差，作为扩大系数α，扩大系数通过标准差的方式求出，公式为：

公式说明：

公式中数值x1，x2，x3，......xN(皆为各自变量的值)，其中μ为各自变量的平均值(算术平均值)，标准差为α。

步骤三、对因变量及各自变量，分别通过公式Z′＝αZ+β求出标准化后的值，Z′为标准数据，β为基准数据，α是扩大系数；

步骤四、保存因变量及各自变量的基准数据及扩大系数，用于后续进行新数据预测时的标准化计算；

通过以上方法把因变量及自变量进行重新计算，从而使最终得出的回归系数更能反映对应因变量与自变量的重要程度；

二、数据横向纵向回归分析

步骤一、按输入的自变量数据按不同聚类数量，多次进行聚类分析，得出多个按不同聚类数量的分析结果；聚类分析可采用K-Means聚类算法，计算聚类的距离可使用Euclidean Distance(欧氏距离)计算方法，公式：

公式说明：

欧氏距离表示两个n维向量a(x11，x12，...，x1n)与b(x21，x22，...，x2n)间的距离，例如二维平面上两点a(x1，y1)与b(x2，y2)间的欧氏距离：

三维空间两点a(x1，y1，z1)与b(x2，y2，z2)间的欧氏距离：

步骤二、对某一特定聚类数量的分析结果，按不同的类别，从中选取自变量，分析选取的自变量与因变量的关系，得出回归系数，再通过回测的方法，计算出准确率，选取准确率最高的自变量与因变量的回归关系；对不同的数据类别采用相同的方法获取准确率最高的回归关系；回归关系可采用最小二乘法多项式曲线拟合，拟合的过程可通过自实现的方式进行，或是通过调用相关通用的拟合工具，直接获取拟合结果，拟合公式为：

公式说明：

假设给定数据点(x_i，y_i)(其中i＝0，1，2，…，m)，为所有次数不超过n(n≤m)的多项式构成的函数类，现求使得满足min公式的P_n(x_i)称为最小二乘拟合多项式，通过代入相关的(x_i，y_i)值并假设min为最小0，可得出n条关于a₀，a₁，a₂，…，a_n的多项式，求解出以上的a₀，a₁，a₂，…，a_n的多元函数，得出a₀，a₁，a₂，…，a_n的具体的值。

步骤三、对分类出来的不同的类别的回归关系进行分析，合并自变量一样、回归系统相差不大的类别，形成统一的回归关系；自变量不同或回归系数相差太大的，形成各数据区域独立的回归关系；

步骤四、重复步骤二、步骤三，从而对不同的数据聚类数量的回归关系的分析，得出各聚类数据下的最优回归关系，回归系数；

三、获取最优对应关系：

步骤一、对各不同的聚类数量分析出来的最优回归关系、回归系统，分析得出最优的准确率，或是最优的前几个的准确率，把分析结果展示给用户，为用户的最终选择提供数据依据；

步骤二、对用户选择的最优结果，需提供自变量与因变量的标准化转换公式，各聚类的中心及分析的回归自变量、回归系数，用于最终的数据预测；

步骤三、用户通过提供的自变量与因变量的标准化转换公式，各聚类的中心及分析的回归自变量、回归系数，在输入新的预测数据时，先进行自变量的标准化，再与各聚类中心进行对比，选取距离最近的数据区域，应用该区域的自变量及回归系统，从而预测出标准化的预测值，再通过标准化公式反推预测的原始值。