螺旋曲面磨削过程中的磨削力预测方法与流程

本发明涉及螺杆磨削加工领域，尤其涉及一种螺旋曲面磨削过程中的磨削力预测方法。
背景技术：
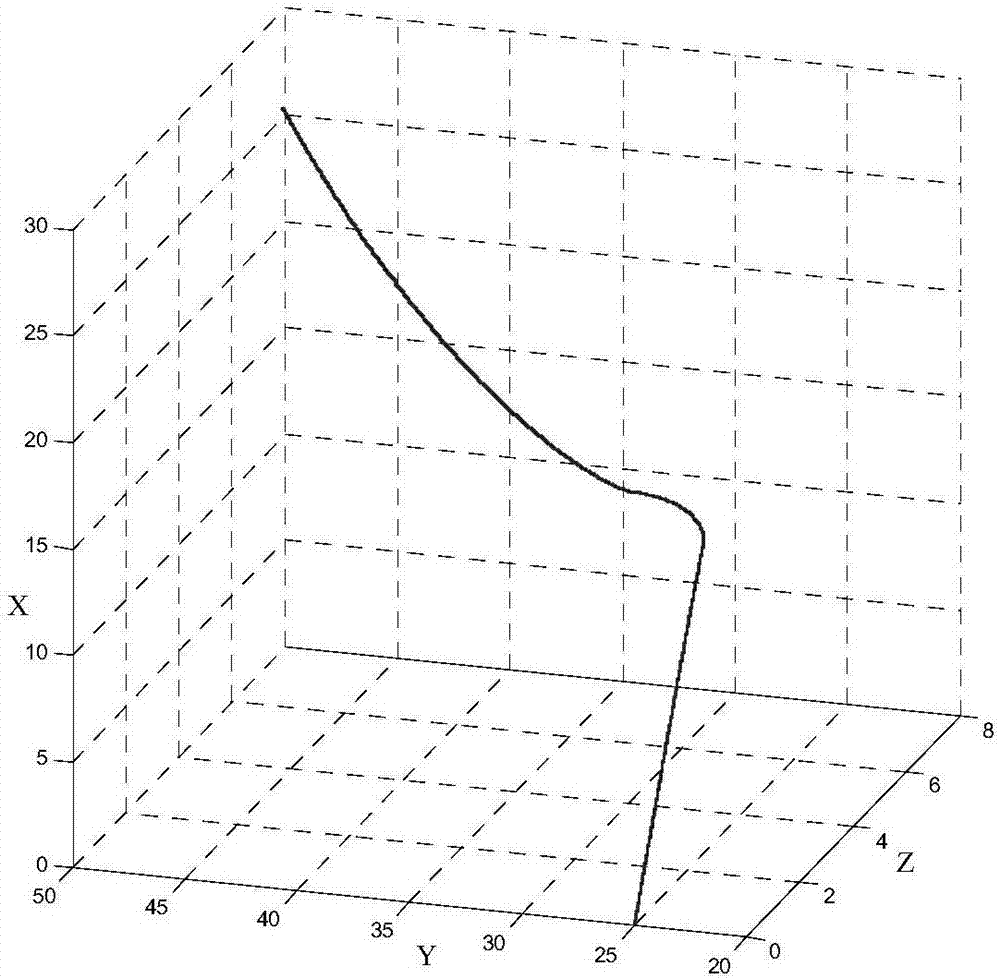
：磨削力在磨削加工过程中是一个极其重要的参数，它不仅影响系统变形、磨削效率、加工精度、表面质量、砂轮耐用度、磨削热量、磨削振动，而且也是超精密磨削机床设计时需要重点关注的参数之一。由于螺杆的磨削加工方法中，砂轮与工件的运动关系较为复杂，现有技术中，通常利用经验公式对螺杆切削力进行计算，而利用公式进行计算前，需先获取砂轮与螺杆的接触线长度，目前普遍采用啮合原理求解接触线及砂轮廓型。由于齿轮啮合原理是运用解析几何的方法通过螺杆与刀具所具有的公法线建立螺杆与刀具的补充条件式，以达到求解接触线及成型刀具齿形的目的，这就要求螺杆齿形曲线在任意点处都具有连续的一阶导数，而实际设计过程中，螺杆端面的齿形曲线一般都是由两条甚至更多的不同类型的曲线组合而成，在曲线与曲线的连接处只能保证曲线的连续性，不能保证曲线在连接点处一阶导数的连续性，使得在运用啮合原理求得的接触线及刀具齿形曲线出现明显的波动情况，影响接触线长度的精确求解。因此，需要一种螺旋曲面磨削过程中的磨削力预测方法，可实现对砂轮磨削区域磨削力的精确计算，该方法可以为螺杆磨床设计、磨削功率的预测等提供所需的理论依据。技术实现要素：有鉴于此，本发明的目的是提供一种螺旋曲面磨削过程中的磨削力预测方法，可实现对砂轮磨削区域磨削力的精确计算，该方法可以为螺杆磨床设计、磨削功率的预测等提供所需的理论依据。本发明的螺旋曲面磨削过程中的磨削力预测方法，包括以下步骤：a.求解砂轮与螺杆接触线的长度以及砂轮与螺杆接触点处的接触弧长lg；b.根据求解得的所述接触线的长度和接触弧长lg，计算砂轮与螺杆在实际参与磨削的磨削面积；c.所述磨削力的大小为：式中，为螺杆的材料系数,其值可由实验测得；为砂轮的平均有效磨粒间隔，可由显微镜观察得到；为砂轮的线速度；vw为螺杆的线速度；ap为磨削深度；de为砂轮的当量直径，x为影响系数；获得材料系数k的实验方法为：磨削实验在普通外圆磨床上进行，砂轮选用60#刚玉砂轮，型号为wa60l6v；工件材料选用合金钢40cr。测力变换装置利用测力顶尖作弹性测力元件，金属式电阻应变片作为变换器，通过信号转换即可测得磨削力，根据其他磨削参数，利用上式即可确定螺杆的材料系数k。影响系数x的取值范围为0.2—0.5，优选0.45；进一步，计算所述接触线长度包括以下步骤：a.求解所述砂轮轴线方向各切削平面的砂轮半径；b.所述砂轮轴线方向各切削平面的砂轮半径对应端点为该时刻砂轮与螺杆的接触点；c.根据所述接触点的坐标，利用离散点拟合方法得到实际接触线模型；d.根据所述实际接触线模型求得所述接触线长度；根据齿轮啮合原理中旋转面刀具构型原理可知，螺杆磨削过程中，每一切削平面必与刀具轴心线交于一点，且与螺杆型面相交并截得一交线,为了不切伤型面，这个交点到与之对应的交线的最短距离就是所选切削平面上的刀具半径，亦即该切削平面上的砂轮半径,因此，求解某一时刻砂轮与螺杆的实际接触线长度，只需求解砂轮轴线方向各切削平面的砂轮半径即可，其对应端点即为该时刻砂轮与螺杆的接触点，根据求得的接触点坐标，利用离散点拟合方法即可得到实际接触线模型，从而求得接触线长度；取初始时刻进行砂轮廓形研究，此时砂轮和螺杆的几何位置关系如图1所示,已知螺杆端面齿形是由一系列离散点(xt,yt)构成，则其螺旋面方程为:式中，s为导程；上面符号表示右旋螺杆，下面符号表示左旋螺杆；由包络原理可知，在螺杆磨削加工过程中，螺杆螺旋面与砂轮回转面之间的相对运动只能有切向的相对滑移，而不允许有法向的冲击或脱离，所以，两曲面的法向相对速度为零，即两曲面接触点处的法向量与相对速度向量所在平面相垂直，此即砂轮与螺杆的接触条件，由齿轮啮合原理中旋转面刀具构型原理可知，砂轮每一切削平面必与砂轮轴心线交于一点，并与螺杆型面相交得一截交线，则砂轮轴向截圆在接触点处的切向量与相对速度向量共面，故砂轮与螺杆的接触条件又可表达为：两曲面接触点处的法向量与砂轮轴向截圆在接触点处的切向量相垂直，即:式中，是砂轮轴的方向向量，是砂轮的径向量(即切削平面与砂轮轴心线之交点同接触点组成的径向量)；如图1所示，选取螺杆坐标系为oxyz，刀具坐标系为ocxcyczc。则两坐标系转换公式为：根据啮合原理，建立砂轮与工件的接触条件，利用matlab即可求得砂轮与工件的实际接触线ls，求得的接触线如图2所示，同时可求得砂轮半径r，从而得到砂轮廓形，所述砂轮半径r为：进一步，计算所述砂轮与螺杆相互接触面的面积的步骤为：a.求解砂轮与螺杆在接触点处的接触弧的长度；b.将所述接触线和所述接触弧构成的空间曲面分割成多个三角形区域；c.分别求解各个所述三角形区域的面积，并将各个所述三角形区域的面积叠加得到所述砂轮与螺杆相互接触面的面积；磨削作用发生时,砂轮与螺杆发生切削作用会产生一个接触作用区域，该接触区域的弧长如图3所示，令ad＝a，则由几何关系可得：代入可得将该式化简得：ap·dw-ap2＝a·dw-2ap·a+a·ds式中，ap为法向磨削深度；dw为螺杆直径；ds为砂轮直径；由于ap很小，且a<ap，故可略去ap二阶即以上的各项，即ap2和2ap·a项可忽略不计，则上式可最终化简为：又ab2＝ad2+bd2，bd2＝ob2-od2，故有由于θ很小，所以接触点处的接触弧长本发明的法向磨削深度ap的求解方法如下：磨削过程中，砂轮圆周与螺杆接触可以等效为外圆磨削，砂轮侧面与螺杆接触可等效为平面磨削。当磨削深度为ap时，砂轮圆周的法向磨削深度即为ap，而砂轮侧面的法向磨削深度并不等于ap。此时砂轮侧面法向磨削深度可由等距线法求得。所谓曲线的等距线，就是从曲线上每一点的法线方向截取相同距离的点的集合。已知某一曲线l，很容易根据其法向矢量得出其等距线l'，如图4所示，若做出曲线l上任意一点j的法向矢量并在法线上截取jj'＝d，则j'就是与曲线l相距d的等距线l'上的一个点。设由图4得：又有：式中：为曲线l上j点的单位法矢量，其矢量坐标为：故等距线l'的方程为：写成坐标表达式为：式中，“+”号表示上等距线，“-”号表示下等距线。任意曲线的切线斜率为：故坐标表达式还可以写成：在螺杆磨削加工过程中，当磨削深度为ap时，砂轮外轮廓沿y轴移动距离为ap，亦即|y'-y|＝ap，因此，由此可得：式中：ap为磨削深度，砂轮径向移动距离；k为砂轮廓形上任意点处的切线斜率；d为砂轮廓形上对应点处的法向磨削深度。砂轮廓形示意图如图5所示，以拉格朗日插值多项式l(x)近似表示通过砂轮廓形上i-1，i，i+1三点(xi-1,yi-1)；(xi,yi)；(xi+1,yi+1)的曲线方程：对上式求导即可求得砂轮廓形任意点的切线斜率k：要求第i点的切线斜率k，只需令上式中x＝xi，即可得到：逐点求出切线斜率k后，即可求得各点处的法向磨削深度d。本发明的螺杆直径dw的求解方法如下：螺杆直径dw由工件型面上各点处的曲率求得，由于螺杆螺旋线上各点处的曲率均相同，故只需求得各螺旋线任一点处曲率即可得到该螺旋线对应的螺杆直径dw，由微分几何相关知识可知，任意曲线l的曲率为：式中：k为曲线l的曲率；l'为曲线l的一阶导；l”为曲线l的二阶导，磨削过程中，螺杆螺旋线方程为：分别求其一阶导和二阶导，为方便计算，令求得的各阶导数表达式中的θ为零(θ为螺杆旋转角度，其值不影响各螺旋线的曲率)，并将结果代入上即可求得各螺旋线的曲率。根据直径与曲率的关系即可求得螺杆直径dw：本发明中砂轮直径ds的求解方法如下：砂轮直径ds由上文中求得的砂轮半径r求得：ds＝2·r将求得的法向磨削深度ap、螺杆直径ds和砂轮直径ds代入即可求得接触点处实际接触弧长lg，利用此方法在matlab中得到的接触弧如图6所示。本发明中所述砂轮与螺杆在实际参与磨削的磨削面积的求解方法如下：结合图2和图6，将得到的接触线和接触点处的接触弧构成的空间曲面分割成若干三角形区域，分别求这些三角形区域的面积，再将其叠加即可得到实际参与磨削的磨削面积，如图7所示，由向量积的定义可知，三角形abc的面积可由下式求得：由于各点的坐标已知，故向量与均可求得，带入上式即可求得三角形abc的面积，将各三角形的面积叠加即可求得实际参与磨削的磨削面积s。最终，本发明的磨削力的计算方法如下：式中，k为与螺杆材料有关的系数；w为平均有效磨粒间隔；vs为砂轮线速度；vw为工件线速度；ap为磨削深度；de为砂轮当量直径，其中，dw为螺杆直径，ds为砂轮直径，为砂轮安装角；x为影响系数，x＝0.2～0.5；又已知实际参与磨削的磨削面积为s，则参与磨削的有效磨粒数为：因此，螺杆磨削的磨削力数学模型为：本发明的有益效果是：本发明的螺旋曲面磨削过程中的磨削力预测方法，在求解磨削力过程中能够避免计算中涉及螺杆的螺旋曲面，因此，本方法求解过程简单，且精度较高。附图说明下面结合附图和实施例对本发明作进一步描述：图1为本发明中砂轮与螺杆瞬时静态位置图；图2为本发明中砂轮与螺杆的实际接触线示意图；图3为本发明中砂轮与螺杆接触点处实际磨削接触弧长的示意图；图4为本发明中利用等距线法求解砂轮法向磨削深度的求解示意图；图5为本发明中砂轮的廓形示意图；图6为本发明中砂轮与螺杆在接触点处的接触弧长度示意图；图7为本发明中砂轮与螺杆的实际磨削面积的求解示意图；图8为本实施例中的a型主动螺杆的齿形曲线示意图。具体实施方式本实施例的螺旋曲面磨削过程中的磨削力预测方法，包括以下步骤：a.求解砂轮与螺杆接触线的长度以及砂轮与螺杆接触点处的接触弧长lg；b.根据求解得的所述接触线的长度和接触弧长lg，计算砂轮与螺杆在实际参与磨削的磨削面积；c.所述磨削力的大小为：式中，为螺杆的材料系数；为砂轮的平均有效磨粒间隔；为砂轮的线速度；vw为螺杆的线速度；ap为磨削深度；de为砂轮的当量直径，x为影响系数；本实施例选取材料为40cr的a型主动螺杆的磨削加工为例，a型主动螺杆螺旋为凸齿，其端面齿形如图8所示；所选取的a型主动螺杆的齿形曲线几何要素值如下表所示：螺杆几何参数参数数值参数数值顶圆直径/mm50根圆直径/mm25导程/mm150节圆直径/mm30中心距/mm115螺杆速度/(m/min)3.14本实施例的砂轮选用60#刚玉砂轮，型号为wa60l6v，其基本参数如下表所示。砂轮基本参数参数数值参数数值砂轮直径/mm200磨削深度/mm0.05砂轮线速度/(m/s)25安装角度/°38.5117本实施例中，根据啮合原理相关知识，利用matlab求得的接触线如图2所示，根据此接触线模型，利用matlab读取其数据点从而求得的接触线长度为34.2819mm，由于砂轮廓形是沿轴向对称的，故此长度为实际接触线长度的一半，实际接触线总长度为68.5638mm。本实施例中，由砂轮基本参数表可知，螺杆磨削过程中，径向磨削深度为0.05mm，即可求得接触线ls各接触点处的切线斜率与法向磨削深度ap，再求得对应接触点处的工件直径dw与砂轮直径ds，将根据求得的ap、dw与ds求得对应接触点处的接触弧长lg。由于选取的接触点数量太多，此处不再一一列出求得的所有接触点的各项参数值。求得的接触线ls与各接触点处的接触弧长lg的真实模型如图6所示(图中所示接触线ls为真实接触线的一半)。将得到的接触线和接触点处的接触弧构成的空间曲面分割成若干三角形区域，利用matlab分别求这些三角形区域的面积，再将其叠加得到实际参与磨削的磨削面积s＝109.318mm2。最终，由所选螺杆与砂轮的参数可确定，k＝170，w＝0.67mm，dw＝30mm，ds＝200mm，ap＝0.05mm，vw＝3.14m/min，vs＝25m/s，x＝0.45，则：ft＝n·ft＝243.5242×0.5830＝141.9746n。最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。当前第1页12