基于熵的双视点无参考立体图像质量客观评价方法与流程

本发明属图像处理领域，涉及基于熵的双视点无参考立体图像质量客观评价方法。

背景技术：

近年来，三维技术逐渐普及，步入大众生活，为观众带来了更好的视觉体验和临场感，但同时也对立体图像的质量提出了更高的要求。由于立体图像的不恰当处理可能会引起观看者的视觉疲劳与不适，因此十分有必要提出一种统一、客观、有效的立体图像质量评价方法对立体图像质量进行准确的预测。

现有的立体图像质量评价方法主要包括基于平面图像质量参数的评价方法和基于人类视觉基本特性的评价方法两种。但是，基于平面图像质量参数的评价方法没有充分考虑人类视觉特性，缺少对立体信息有效利用，因而难以投入实践。现有的基于人类视觉基本特性的评价方法中最重要的一步是立体匹配，但是如何有效地提取立体信息，合理地进行匹配，仍然是立体图像领域关注的焦点。因此，很有必要建立一个以立体图像基本信息为基础，又充分考虑人类视觉特性的立体图像质量客观评价方法。

此外，鉴于现有的立体图像质量评价方法需要原始的参考图像作为评价依据，因此具有很大的局限性，所以无参考(即不需要原始的参考图像对做评价依据)立体图像质量评价方法应运而生。

技术实现要素：

本发明的目的在于克服现有技术的上述不足，提供一种能够充分考虑双视点特性的无参考立体图像质量客观评价方法；本发明的技术方案如下：

一种基于熵的双视点无参考立体图像质量客观评价方法，每个失真立体图像对由左图和右图组成，设失真图像对为(t_l,t_r)，包括以下步骤：

第一步：模拟人类视觉特性，对失真图像对的左图和右图分别进行二维Gabor滤波，得到左图和右图的加权因子:W_L(x,y)和W_R((x+d),y)，其中，(x,y)为像素点坐标，d表示对右图进行视差补偿的像素点横坐标差值；

第二步：将失真图像对(t_l,t_r)进行加权运算，得到失真图像对的视觉感知图V(x,y)；

第三步：利用奇异值分解算法K-SVD进行字典学习；

第四步：利用正交匹配追踪算法OMP对V(x,y)进行稀疏表示，得到相应的系数矩阵C；

第五步：对视觉感知图像V(x,y)稀疏表示后的系数矩阵C进行求熵操作，得到其熵E；

第六步：对立体图像库中的每一组失真图像对进行第一步至第五步操作，设立体图像库中有Q组立体图像对，可以得到Q组图像对各自的熵E；

第七步：利用支持向量机SVM对图像库中图像对的熵及相应的主观评价值(DMOS)进行训练，具体如下，随机选择Q×80％幅图像对的熵和DMOS用于训练，得到相应的熵-DMOS模型；

第八步：对任意一组失真图像对，进行第一步至第五步操作，得到对应的熵；根据第七步中得到的熵-DMOS模型，利用SVM对该图像对的客观预测值进行预测，到最终的客观预测值。

本发明所提出的立体图像客观质量评价方法以视觉感知图像的熵为基础，通过稀疏表示的方式，把熵与视觉感知过程相结合，充分模拟了立体图像主观评价的过程，得到的立体图像质量客观评价结果与主观评价结果具有很高的一致性，能够较为准确的反映图像的质量。

附图说明

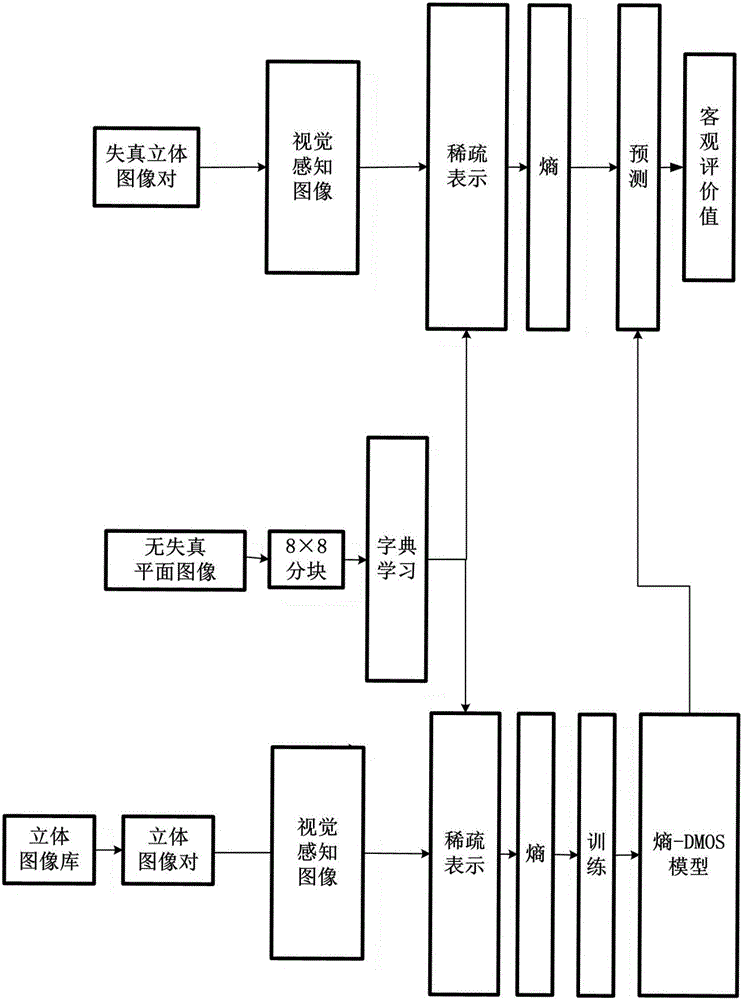
图1本发明的流程图。

具体实施方式

基于熵的双视点无参考立体图像质量客观评价方法，每个失真立体图像对由左图和右图组成，设失真图像对为(t_l,t_r)，包括以下步骤：

第一步：模拟人类视觉特性，对失真图像对(t_l,t_r)的左图和右图分别进行二维Gabor滤波，得到相应的能量响应，并进行卷积和处理，经归一化运算分别后得到左图和右图的加权因子:W_L(x,y)和W_R((x+d),y)，其中，(x,y)为像素点坐标，(x+d)表示视差补偿，d表示对右图进行视差补偿的像素点横坐标差值；计算方法如下

(1)二维Gabor滤波器为：

其中，G(x,y,σ_x,σ_y,ζ_x,ζ_y,θ)是Gabor滤波器的响应值，x,y,σ_x,σ_y,ζ_x,ζ_y,θ分别代表Gabor滤波器的x方向、y方向、椭圆高斯包络沿x方向的标准差、椭圆高斯包络沿y方向的标准差、x方向的频率、y方向的频率和相位角，R₁＝xcosθ+ysinθ，R₁＝xcosθ+ysinθ；

(2)Gabor滤波器的能量响应是以3.67次/度的空间频率循环，叠加滤波器沿水平、竖直和两个对角线方向的幅度响应得到的；

(3)能量响应经卷积和计算后得到GE_L(x,y)与GE_R(x,y)，并进行视差补偿得到GE_R((x+d),y)，其中，(x+d)表示视差补偿，d表示对右图进行视差补偿的像素点横坐标差值；

(4)经公式(2)和(3)所定义的归一化运算得到左图和右图的加权因子W_L(x,y)和W_R((x+d),y)。

第二步：将失真图像对为左右图(t_l,t_r)进行加权运算，得到失真图像对的视觉感知图V(x,y)，计算如公式(4)所示；

V(x,y)＝W_L(x,y)×t_l(x,y)+W_R(x+d,y)×t_r((x+d),y) (4)

第三步：字典学习。选取P幅m×n尺寸无失真的平面参考图像，每个图像分割为8×8的图像块M＝[m/8]×[n/8]个，其中[x]表示不大于x的最大整数。并将每个8×8的图像块按列排成一列，标记为x_i(64×1)。这样每个无失真参考图像都可以转换为(64×1)×M的二维矩阵。P幅无失真平面参考图像通过上述处理，可以得到一个64×(M×P)的二维矩阵。随后，根据如下公式，可以求得相应的字典D。

在求解的过程中，字典的求解利用K-SVD(奇异值分解)算法，迭代次数设置为40次，字典稀疏基(原子)的数目为256。

第四步：对失真图像对的视觉感知图V(x,y)进行稀疏表示。假定V(x,y)大小为m×n。利用第三步中得到的字典D，对V(x,y)进行稀疏表示，求得相应的系数矩阵C。此过程中，采用的算法是OMP(正交匹配追踪)算法，迭代次数为14次。每组失真图相对的左(右)图系数矩阵的大小为256×([m/8]×[n/8])×14的三维矩阵。

第五步：对视觉感知图像V(x,y)稀疏表示后的系数矩阵C进行求熵操作，得到其熵E。具体操作如下：

用代表稀疏表示第i(1≤i≤14)次迭代中，第j(1≤j≤256)个稀疏基中系数的具体值。

对应概率分布函数如下：

根据香农公式，其熵如下：

其中，k是稀疏基的个数，本发明中k＝256。按照上述操作，求得V(x,y)的熵E，E为1×14的行向量。

第六步：对立体图像库中的每一组失真图像对进行第一步至第五步操作。假定立体图像库中有Q组立体图像对，可以得到Q组图像对各自的熵。

第七步：利用支持向量机(SVM)对图像库中图像对的熵及相应的主观评价值(DMOS)进行训练。具体如下，随机选择Q×80％幅图像对的熵和DMOS用于训练，得到相应的熵-DMOS模型。

第八步：对任意一组失真图像对，进行第一步至第六步操作，得到对应的熵。根据第七步中得到的熵-DMOS模型，利用SVM对该图像对的客观值进行预测，到最终的客观预测值。