一种引入非线性弹簧的微型桩基‑土动力响应求解方法与流程

本发明属于土建领域，具体涉及一种引入非线性弹簧的微型桩基-土动力响应求解方法。

背景技术：

目前分析单桩-土相互作用的方法主要有连续介质解析法、Wenkler地基梁法、有限差分法、有限元和边界元法等，这样的分类方法取决于模拟桩周土的方法。连续介质解析理论法能够正确表示几何阻尼和土层共振现象，但必然受到线弹性或粘弹性等假设所限制。对于有限元法来讲，如果要准确模拟并得到精确的结果，则代价往往是巨大的。就如一个桩土动力相互的模型的计算往往需要几万个或者十几万个单元，这也就需要将单元划分的较细，而计算时间步长取决于模型中最小单元的尺寸。这样导致一个动力模型2～4s的时域计算得花费好几天的时间，这对于设计要求显然是不经济、不适合的。Wenkler地基梁法的提出自于1867年，当时他提出了一种理想化的土介质模型，即建筑地基基底表面土应力随荷载线性变化的假设。在此基础上经过一百多年演化出了多种越来越来越精确的模型。现行的Wenkler地基梁模型通过质量、刚度、阻尼对桩-土相互作用进行考虑。如浙江大学的胡安峰等利用Wenkler地基梁模型推得了桩-土动力相互作单层土和多层土的横向动力响应的解析解。虽然其具有计算效率高等特点，但其也有一定的局限性，如不能描述土的屈服发展和土中应力波的传递。为此，提出了一种引入非线性弹簧的微型桩基-土动力响应求解方法，该方法基于Wenkler地基梁模型，通过对建立的动力平衡控制方程引入所得到经验p-y上骨架作为弹簧刚度，得到考虑非线性弹簧刚度的微型桩-土相互作用横向动力响应半解析解，相比现行常用的计算方法，其具有简化、效率高、精确等优点。

技术实现要素：

本发明的目的是提供一种引入非线性弹簧的微型桩基-土动力响应求解方法，该方法是将非线性弹簧刚度来代替桩周土的刚度，是解决微型单桩-土侧向动力响应问题的一种新型方法。

为实现上述目的，本发明采用以下技术方案：一种引入非线性弹簧的微型桩基-土动力响应求解方法，其特征在于，包括以下步骤：步骤一：假定土体是均匀的、各项同性的具有非线性的粘弹塑性连续介质，非线性规律按照经验p-y骨架曲线给出；步骤二：假设截面为圆形，其它截面进行截面变换折算成圆形截面，考虑桩体的水平运动和变形；步骤三：考虑承台的质量和桩-土相对位移；步骤四：假定荷载作用为简谐波，计算其稳态下的响应情况。

与现有技术相比，本发明考虑的是桩与土两者的非线性计算方法，对现有求解桩基-土动力响应方法的进一步完善，考虑了桩身周围土体的非线性作用，且引入非线性弹簧来模拟土对桩的响应；基于Wenkler地基梁模型，通过对建立的动力平衡控制方程引入所得到经验p-y上骨架作为弹簧刚度，得到考虑非线性弹簧刚度的微型桩-土相互作用横向动力响应半解析解，因此本发明具有简化、效率高、精确等优点。

附图说明

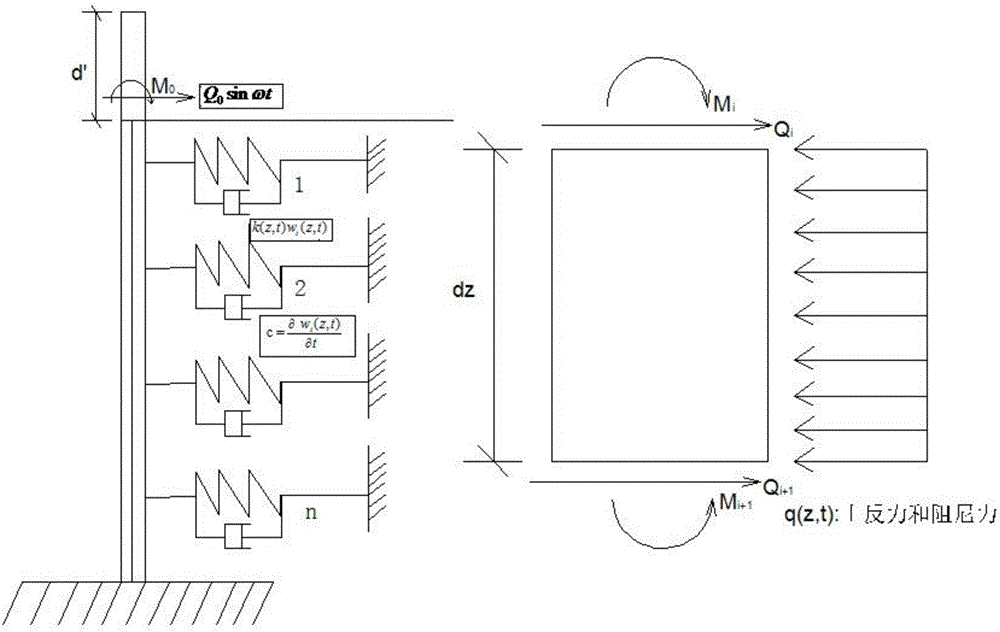
图1为桩土分析模型图。

图2为稳态下的位移响应求解流程图。

具体实施方式

下面结合附图和具体实施例对本发明做进一步解释说明。

本发明提供一种引入非线性弹簧的微型桩基-土动力响应求解方法，该方法所要解决的技术问题是针对以上传统的桩基-土动力相互作用计算方法的不足及设计偏不安全而提出的一种新型方法，为使分析对象更加简明，将分析模型简化成如说明书附图1所示的形式。要对这一分析模型进行连续解得推理并得出响应的解析解是非常困难的，为使解析过程更加方便，则需进行如下简化：

(1)假定土体是均匀的、各项同性的具有非线性的粘弹塑性连续介质，非线性规律按照经验p-y骨架曲线给出；

(2)假设截面为圆形，其它截面可进行截面变换折算成圆形截面。桩体暂假定为线弹性的欧拉梁，只考虑桩体的水平运动和变形；

(3)考虑承台的质量和桩-土相对位移；

(4)假定荷载作用为简谐波，计算其稳态下的响应情况。

具体计算包括以下步骤：

分析模型的建立

为让本发明的上述特征和优点能更明显易懂，下文对计算方法模型的建立并配说明书附图1，作详细说明如下：

首先将桩和土分成n层，表层土为第1层土，土表层为原点，土深为h，每层厚度dz为相应的计算厚度。图中i层桩土产生的水平振动相对位移为w_i，取坐标向下为正，桩的最低层为第n层。原点为土表面位置，将土表面以上的力转移到土表面的桩点位置。Q₀sinθ为桩顶受到的动荷载。

选取经验p-y上骨架曲线为每层的土反力形式，并对其进行简化得土弹簧刚度如式(1-1)所示：

其中：d为桩径大小，z为土的深度，w(z,t)为埋深为z，加载时间为t时的桩土产生的水平振动相对位移；k(z,t)为埋深为z，加载时间为t时的土压缩刚度；

然后对附图1中的桩体微元作水平动力平衡分析，得动力平衡控制方程式(1-2)：

其中：ρ和A分别为桩体的材料密度和横截面面积，d本为微型桩体的有效计算宽度，在这里取微型桩的直径d，δ(i-1)为广义狄克拉函数，c根据前人的成果进行取值，为而其中E_s、ρ_s、β_s、v_s分别为该层土的弹性模量、密度、阻尼比和泊松比，ω为荷载激励的频率，E J为桩身的抗弯刚度，。

对式(1-2)化简得：

令得：

边界条件：

(1)桩顶自由，则桩顶的弯矩为剪力变量为则有：

(2)桩底固定，则桩底的变形为零，转角也为零，则有：

初值条件：

稳态激振的求解

方程(1-4)为非线性偏微分方程，主要因为刚度k是一个随深度和刚度变化的值，这导致解此偏微分方程的难度大大增加，为方便求解，通过对弹簧刚度k进行多次迭代的方法求得最终的w值。

首先将各土层的刚度k设为一个定值，此时动力平衡方程变为线性。非齐次微分方程的解可有其次的通解加上非齐次的特解得到，因此先解出相应的其次方程的解，其次方程如(1-8)

对于稳态激振时，式(1-8)的解设为w(z,t)＝U(z)·e^iωt，将其带入到式(1-8)中，得水平向平衡控制式为(1-9)：

对式(1-9)进行简化得：

其中：

解微分方程式(1-10)得：

对(1-11)求导得(1-12)-(1-14,)：

U”(z)＝-2C₁λ²e^λz sin(λz)+2C₂λ²e^λz cos(λz)+2C₃λ²e^-λz sin(λz)-2C₄λ²e^-λzcos(λz)

(1-13)

结合边界条件(1-5)和(1-6)得系数C₁、C₂、C₃、C₄分别为：

其中：

因此各稳态响应方程如下：

w(z，t)＝(C₁e^λz cosλz+C₂e^λzsinλz+C₃e^-λz cosλz+C₄e^-λz sinλz)e^iωt

(1-15)

上式(1-15)～(1-17)是基于稳态下土层刚度不变时推导得到的，这与假定土体进入塑性状态不符，为得到考虑土体塑性的微型桩-土体系动力响应解，则引入经验p-y上骨架曲线，通过多次迭代得到每个时刻的最终位移、弯矩和剪力等。以位移的求解为例，具体步骤如说明书附图2所示：赋予w一个很小的初始值w₀；求取w_j+1：

其中

0≤j≤n；判断是否|w_j+1-w_j|≤ξ，若是则w(z_i,t_k)＝w_j+m，否则返回步骤S32；ξ为位移阀值，m为迭代的增量次数，t_k为加载的时间。

较佳的，w₀＝0.1×10^-4m。

以上所述仅为本发明的较佳实施例，并不用以限定本发明，在不脱离本发明基本构思的前提下所做的若干等同替代和变型，均应包含在本发明的保护范围之内。