桩基螺旋埋管在地下水渗流条件下的温度响应计算方法与流程

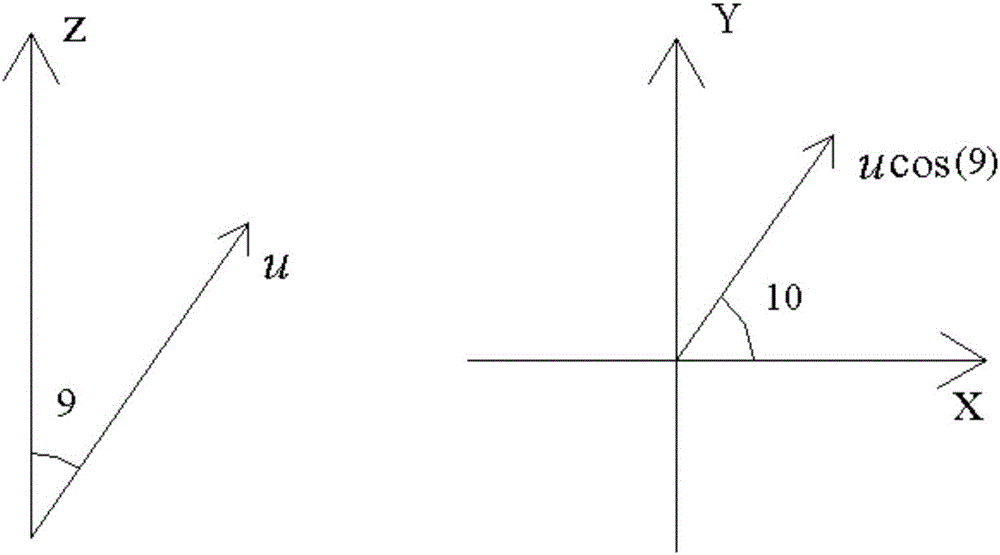
本发明属于建筑环境与能源应用专业工程
技术领域：
，具体涉及一种桩基螺旋埋管在地下水渗流条件下的温度响应计算方法。
背景技术：
：地源热泵技术以地下介质为冷热源，夏季和冬季分别向地下排热和从地下吸热。地下介质的温度全年波动较小，是一种理想的冷热源，因此该类型热泵具有节能及环保的优势，属于可再生能源空调系统，受到了广泛应用。地热换热器部分是地源热泵系统区别于其他类型热泵系统的主要标志，目前常采用钻孔并埋设U型换热管的方式，但由此造成了初投资过高和需要一定量地面面积布置钻孔，这两大缺点成为制约地源热泵发展的主要障碍。随着人们对地热换热器研究的不断发展，建筑物的承载构件即桩基，被考虑用来埋设换热管，由此产生了一种新颖地热换热器，称之为“桩埋管换热器”。桩基的直径要远大于钻孔的直径，且内部通常布置螺旋管而非U型管，故每米桩埋管的换热能力要明显强于钻孔埋管。因建筑物的桩基数量有限，整个系统的地热换热器可由能量桩和钻孔埋管共同组成，能量桩最大程度的承担部分冷热负荷，余下的负荷由钻孔埋管负责，因此钻孔的花费大大降低，且布置钻孔的地面面积也会减少。由于桩基的长度超过十米甚至达到几十米，地下水的渗流现象不可忽视，尤其是水力梯度较大或地下水资源丰富的地区，渗流的影响更要引起重视。当地下水流经能量桩时，桩基和周围地下介质的传热模式将由单一的纯导热转变为含有导热和对流的复合换热。地下水的流动缓解了桩基周围的热积累，改善了桩埋管的传热性能，提高了每米桩埋管的换热量。桩埋管在传热过程中，周围介质受其影响温度不断变化，当地下水渗流现象出现时，地下介质的温度响应程度受地下水的影响被减缓，意味着地下水降低了桩埋管的传热对地下空间的影响。目前，对桩埋管在地下水渗流条件下的研究较少，尚未有计算地下水在地下空间内以三维速度进行渗流时地下介质温度响应的方法。技术实现要素：本发明为了解决上述问题，提出了一种桩基螺旋埋管在地下水渗流条件下的温度响应计算方法，本发明所提出的这一计算方法，有利于掌握地下介质的温度变化以及地下温度场的分布情况，使人们能够深入认识地下水渗流对桩埋管换热的影响。为了实现上述目的，本发明采用如下技术方案：一种桩基螺旋埋管在地下水渗流条件下的温度响应计算方法，包括以下步骤：(1)在地下水以三维速度流经无限大均匀介质的前提下，确认处于介质中的以一定强度散热的点热源在介质中任意一点处引起的温度响应；(2)构建地下水以三维速度流经单个桩埋管时的温度响应传热模型，获得当具有一定螺旋间距、螺旋半径和长度的换热管埋设于桩基中形成桩基螺旋埋管地热换热器后的半无限大介质中除螺旋管外任意一点的温度响应；(3)在钻孔埋管换热器周围布置测点进行温度响应测试，并利用有限长线热源渗流模型，反向推算地下水的流速，结合构建的响应模型，计算温度响应结果。所述步骤(1)中，根据点热源在无限大介质中以纯导热方式产生温度响应的格林函数，对格林函数加以改变，得到地下水以三维流动的方式流经地下介质时点热源引起的温度响应。所述步骤(1)中，在地下水以三维速度流经无限大均匀介质的前提下，地下介质分布均匀且其孔隙率一致，根据孔隙率、地下固态介质的体积比热容、地下水的体积比热容、地下固态介质和地下水的导热系数计算某段时刻内位于(x’,y,’z’)的点热源在无限大空间中任意一点(x,y,z)引起的温度响应。所述步骤(2)中，螺旋换热管布置于桩基后，地下水以三维的流速流经单个桩埋管时，综合考虑导热和对流的影响，建立能量方程，列出所对应的初始和边界条件；将地面的恒温对有限长桩基螺旋埋管的影响加以考虑，并考虑了螺旋管和桩基的各个参数在换热过程中的影响。所述步骤(2)中，利用虚拟热源法，即认为在地下介质中存在恒定发热的螺旋管，在以地面为对称面的虚拟的另一半无限大介质中，有恒定吸热的螺旋管，即同时存在着螺旋线热源和螺旋线热汇，得到了有限长的桩基螺旋埋管地热换热器在三维地下水渗流条件下对地下介质产生的温度响应表达式后，即可计算出三维地下水流经单个桩基螺旋埋管时，地下介质中除换热管外任意一点在任意时刻的温度响应。所述步骤(2)中，根据单个桩基螺旋埋管在地下水渗流条件下，在地下空间内除螺旋管外任意点(x,y,z)所引起的温度响应，考虑若干个桩基埋管在该点引起的温度响应的叠加，结合桩埋管之间的间距、排列方式，从而确定桩埋管群体在该点引起的温度响应。所述步骤(3)中，具体过程包括：(3-1)沿钻孔埋管换热器周围及深度方向均匀布置测点，在测点处安装热电偶或热电阻。(3-2)设定好地下水流速和方向角的范围，从设定范围内抽取数据；(3-3)采用钻孔埋管的地下水渗流计算模型，计算钻孔周围布设的点的过余温度；(3-4)计算每个布置点的理论计算值与实际值的方差，判断是否有符合设定值个数的布设点的方差和达到最小值，如果是，则输出此时的地下水流速的大小和方向，如果不是，则继续从地下水流速大小和方向的范围内抽取数值进行迭代计算。所述步骤(3-1)中，在钻孔埋管换热器周围布置耐腐蚀的热电偶或热电阻，采用数据采集仪进行记录所布置点的温度随时间的变化。所述步骤(3-2)中，将流速大小和角度在各自的范围内不断抽取，代入有限长线热源渗流模型进行计算。所述步骤(3-3)中，利用钻孔埋管在地下水渗流条件下比较成熟的有限长线热源渗流模型，结合自步骤3-2中不断抽取来的地下水流速大小和方向，计算获得钻孔周围所布置点的温度响应值。所述步骤(3-4)中，使方差和对地下水流速的大小u和两个方向角α和β都取一阶导数，三个一阶导数都同时小于设定值时，认为一阶导数近似为零，此时，对于该点的方差和已达到最小。本发明的有益效果为：(1)桩基螺旋埋管作为地热换热器在与地下介质进行换热过程时，当地下水的渗流作用被考虑之后，地下介质中除换热管外的任意位置处在任何时刻的温度变化可以直接通过计算获得，而不必在现场埋设数量较多的热电阻或热电偶。通过获得一个桩基埋管在地下水渗流作用下的温度响应的计算方法，进而掌握在地下水渗流条件下若干个桩埋管引起的地下介质的温度变化；(2)地下水的渗流增强了地热换热器的换热能力，每米换热器的换热量得到增加，可以通过本发明的技术方案，揭示桩基螺旋埋管的换热量与地下水流速之间的关系，分析不同地下水流速对具有不同几何尺寸参数的桩基埋管的影响；(3)地下水的渗流作用，改善了整个地源热泵空调系统的经济性，这是由于地下水渗流使得桩基埋管承担的换热量增加，因而钻孔埋管承担的冷热负荷会减少，钻孔的投资费用会降低。采用桩埋管的主要目的是为了降低系统的初投资，进一步考虑渗流的影响，更是对桩埋管研究的进一步贡献；(4)为了配合本发明计算方法的应用，地下水的渗流速度必须要首先得出，通过提出反向推理计算法，可以不必通过直接测量而得知地下水流速。渗流速度通常较小，直接测量的困难较大，且地下环境复杂不易布置测量流速的仪器。因此获得地下水渗流速度也是本发明的一个重要意义；(5)地下介质中任意一点的温度响应，是具有一定排列形状的桩埋管群在地下水渗流条件下共同作用的结果，在同一点处和相同的渗流速度下，不同形状排列的管群所产生的作用并不相同，可以根据温度响应的计算方法，分析各个排列方式的管群在相同地下水渗流速度时，所产生的温度响应的区别，从中优化管群的排列方式。附图说明图1为地下水渗流条件下桩基螺旋埋管换热时的示意图；图2为地下水渗流速度与坐标轴的夹角示意图；图3为钻孔周围布置测点示意图；图4为反向推理计算法的流程示意图。其中：1螺旋管起点h1,2地下水渗流，3建筑物桩基，4螺旋换热管，5地下介质，6螺旋管终点h2,7螺旋管间距b,8地下水渗流，9地下水的渗流速度与Z轴的夹角α，10地下水渗流速度在XOZ面的投影与X轴的夹角β，11钻孔，12钻孔周围布置的测点。具体实施方式：下面结合附图对本发明作进一步说明。桩基和埋设于其内部的螺旋换热管皆具有相应的几何尺寸，桩基的直径及长度、螺旋直径、螺旋间距、螺旋长度等参数都对桩埋管的换热产生影响。地下介质可认为是具有相同热物性参数的均匀介质。本发明提出地下水渗流条件下能量桩产生的温度响应的解析计算法，对于具有不同几何参数的桩基螺旋埋管，当地下水流过时，在导热与对流复合换热的作用下，地下介质中除螺旋换热管外任意一点处的温度响应可以获得。此外，地下水的流速是包含大小和方向的矢量，直接测量流速是一项非常困难的工作，且地下水的渗流速度较小，不易测得。因此，本发明了一种反向推理法用以推算地下水的渗流速度，包括其大小和方向。将获得的地下水流速代入计算地下介质温度响应的方法中，可得到地下介质任意一点任何时刻的温度变化。根据本发明的内容，可分析桩基螺旋埋管的换热量与地下水流速之间的关系。桩基螺旋埋管换热器在地下水渗流条件下的换热，要明确其相关的尺寸参数以及地下介质的热物性参数。图1为桩基埋管在地下水渗流条件下的示意图，循环液往返于螺旋换热管和热泵机组之间，其流经螺旋管时的进出口温度、流量可用温度计和流量计测得从而计算出桩基埋管每米的换热量ql。地下介质分布均匀且其孔隙率为ε。ρscs是地下固态介质的体积比热容，ρwcw是地下水的体积比热容。ks和kw分别表示地下固态介质和地下水的导热系数。因此，地下介质总的体积比热容和导热系数如公式(1)所示：k=ϵkw+(1-ϵ)ksρc=ϵρwcw+(1-ϵ)ρscs---(1)]]>地下水渗流的速度u为矢量，包括大小和方向，其在x,y和z方向上的分速度分别为u1,u2和u3。螺旋管埋设于桩基中，螺旋半径和间距分别为r0和b,代表其螺旋角度。换热管离地面的起始和终点位置分别为h1和h2,因此所对应的螺旋角度分别为：和螺旋管沿桩基表面以一定的间距和角度螺旋盘绕。ql为每米桩埋管换热器的传热量。在实际换热过程中，循环液沿螺旋管进入然后沿中心的直管段流出返回热泵机组。地下介质的初始温度和非初始温度分别为t0和t，在整个换热过程中，地面的温度保持恒定，且地下介质和地下水的热物性参数保持不变。(x’,y,’z’)代表螺旋管热源上任意一点的坐标，(x,y,z)则表示除热源外地下介质中任意一点的坐标。τ是指换热过程中的任意时段；θ＝t-t0表示过余温度，又可称之为温度响应，即桩埋管在地下水渗流条件下，所导致的地下介质中任意一点任意时刻的温度变化。根据分析，对桩基螺旋埋管地热换热器在地下水渗流条件下的传热过程建立数学模型，里面包括能量方程和相应的初始及边界条件。如公式(2)所示,r为地下介质中任意一点距离桩基埋管中心轴线的径向距离，δ(x-x’,y-y’,z-z’)为狄拉克函数。根据公式(2)，可计算得到地下介质中除换热管外任意一点在任意时刻的温度响应，这也是在地下水渗流作用下，桩基螺旋埋管和地下介质进行热交换时对地下空间造成的热影响。桩基和螺旋管的几何参数可以任意取值，只要某个桩基螺旋埋管换热器的结构尺寸和地下水的流速已知，则可根据公式(2)得到温度响应的值；这也是本发明的发明意义所在，可用来计算任意尺寸的桩埋管在不同地下水渗流速度时所产生的温度响应。建筑物的桩基有若干个，意味着桩基螺旋埋管换热器的个数若干，若不考虑钻孔埋管换热器，地下介质中的任意一点温度响应则是由这若干个桩埋管产生的温度响应在该点处的叠加，故可根据一个桩埋管在地下水渗流时的计算方法，叠加若干个桩埋管产生的总的温度响应。地下水流速为矢量，大小和方向取决于当地的水力梯度，其大小范围通常在10-8m/s～10-1m/s之间。由于渗流速度较小，不易直接采用设备测量，一种全新的反向推理法在本发明中被提出。目前钻孔埋管在地下水渗流时的研究已较为成熟，有限长线热源渗流模型可用来计算钻孔埋管地热换热器在地下水渗流条件下周围地下介质中的温度响应，为了反向推算地下水的流速大小和方向，可采用理论计算加实验测量的方式。地下水的渗流大小虽未知，但根据当地的水力资料，可知其在一定范围内，因此首先设定地下水流速大小的范围。另外，地下水的方向亦未知，由于水力梯度通常是呈三维分布，地下水的渗流速度也是三维分布，即其沿x,y和z方向均有分速度。根据图2所示，流速的方向主要由两个参数决定，即流速与z轴的夹角α以及流速在xoy面上的投影与x轴的夹角β，这两个角度的具体值虽未知，但α和β的范围分别为0≤α≤π和0≤β≤2π。在钻孔埋管的周围均匀布置五个点，如图3所示，五个点距离钻孔中心的距离相等且彼此之间的夹角相等，这是在一个水平面沿钻孔埋管周围布置五个点；沿钻孔深度方向上每隔几米就在对应的水平面上均匀布置五个点，在这些点处埋设热电偶，温度响应随时间的变化可用热电偶获得。另外，将流速大小和角度在各自的范围内不断抽取，代入有限长线热源渗流模型中，每个点处计算得到的温度响应与热电偶测得的温度响应的差值达到最小时，此时从范围中抽取的流速大小和角度正是实际的地下水渗流速度的值；所对应的计算如公式(3)所示：S=Σk=1n(θcal,k-θexp,k)2---(3)]]>k表示采集数据阶段内，每一时刻的序号。θcal,k表示在第k时刻采用线热源渗流模型数学公式计算得到的温度响应，而θexp,k则表示在第k时刻实验采集到的温度响应值。在实验过程中设定时间间隔，每隔一定时间，数据采集仪会记录一次数据，包括从k＝1时刻到n时刻的实验数据。公式(3)给出了所布置的点中任意一点在采集数据的时间阶段内实验值与理论计算值的方差和。当在钻孔周围布置的大多数的点方差和同时达到最小值时，此时从流速的大小和方向的范围内抽取的数值即为实际值，意味着通过不断的迭代进行反向推理计算，直到方差和的值达到最小时可获得地下水的流速大小和方向。根据流经螺旋换热管的循环液的进口温度t1和出口温度t2，以及循环液的质量流量m和螺旋管在桩基中的深度h2-h1，计算出每米螺旋管的换热量，具体如公式(4)所示：ql＝Cp×m×(t2-t1)/(h2-h1)(4)地下水以三维的方式进行渗流，其渗流速度u沿x,y和z方向的速度量分别为u1,u2和u3，螺旋管的半径和间距分别为r0和b,螺旋角度为换热管离地面的起始和终点位置分别为h1和h2,桩基的直径和深度分别为rp和H。在布置换热管的过程中，螺旋管的直径通常要略小于桩基的直径，且该管和桩基底部之间要保持一定间距。对传统的格林函数进行变形，可获得地下水以三维流动的方式流经地下介质时点热源引起的温度响应：T(x,y,z,τ;x′y′,z′,τ′)=18[πa(τ-τ′)]3/2exp{-[x-x′-U1(τ-τ′)]2+[y-y′-U2(τ-τ′)]2+[z-z′-U3(τ-τ′)]24a(τ-τ′)}---(5)]]>公式(5)为在纯导热基础上变形后的新格林函数，U1、U2和U3分别为地下水沿x,y和z轴的分速度。对于在地下水渗流时的多孔介质中，位于(x’,y,’z’)的点热源，从τ’时刻开始发热直到τ时刻在无限大空间中任意一点(x,y,z)引起的温度响应表达式仍然采用公式(5)，只是此时公式(5)中U1＝u1ρwcw/ρc,U2＝u2ρwcw/ρc,U3＝u3ρwcw/ρc。而u1、u2和u3为实际地下水的三个分速度。为了获得桩基螺旋埋管在三维空间中产生的温度响应，在本发明方案的实施过程中，可首先将桩埋管假设为无限长，沿深度方向的传热可被忽略，而只考虑水平面x和y方向的传热，意味着地面的影响被忽略。根据公式(2)和(5)，可得出无限长的桩埋管在地下水渗流条件下的温度响应计算公式，如公式(6)所示：θi=ql2πρc∫-∞+∞dz′∫02πdφ′∫0τ18[πa(τ-τ′)]3/2·exp[-[x-x′-u1(τ-τ′)]2+[y-y′-u2(τ-τ′)]2+[z-z′-u3(τ-τ′)]4a(τ-τ′)]dτ′---(6)]]>在公式(6)的基础上，进一步考虑有限长桩埋管在地下水渗流时的换热，地面的温度恒定不变，螺旋管在桩基内的起始位置分别为h1和h2。无限长桩埋管的结果为有限长的研究奠定了基础。根据公式(2)和(5)，采用虚拟热源法，所谓虚拟热源法，即在地下介质中存在恒定发热的螺旋管，在以地面为对称面的虚拟的半无限大介质中，有恒定吸热的螺旋管。从而存在着所谓的螺旋线热源和螺旋线热汇。单个桩基螺旋埋管在地下水渗流条件下，自时刻τ’开始与地下介质进行换热，到τ时刻时在地下空间内除螺旋管外任意点(x,y,z)所引起的温度响应的计算公式为：其中，z’＝z’。公式(7)列出了一个有限长桩埋管在地下水渗流时引起的温度响应，而对于任意一点，其温度响应是由若干个桩基埋管，或者说是有桩基埋管群在该点引起的温度响应的叠加，因此，桩埋管群体在任意一点(x,y,z)引起的温度响应表达式(8)为：θtotal=Σi=1nθi=Σi=1nql2πρc∫0τdτ′∫02πdφ′18[πa(τ-τ′)]3/2exp[-[x-(xi+r0cosφ′)-U1(τ-τ′)]2+[y-(yi+r0sinφ′)-U2(τ-τ′)]24a(τ-τ′)]∫h1h2{exp[-[z-z′-U3(τ-τ′)]24a(τ-τ′)]-exp[-[z+z′-U3(τ-τ′)]24a(τ-τ′)]}dz′---(8)]]>因为桩基在排列过程中，每个桩埋管沿深度方向的坐标相同，区别在于它们的水平面坐标，即x和y方向的差异。由桩埋螺旋管在地下水渗流作用下的温度响应计算公式可知，地下水的流速必须要得出，才能计算出温度响应值。根据介绍的反向推理计算法，相应的反向计算流程如图4所示。沿钻孔深度方向布置耐腐蚀的热电偶或热电阻，采用数据采集仪进行记录所布置点的温度随时间的变化。每个点的理论计算值与实验数据差值的方差和达到最小时，此时从地下水流速的大小和方向里抽取的数值即为实际的地下水流速值。由于布置在钻孔周围的点数较多，沿深度方向每隔几米就均匀布置五个点，每一层的五个点的方差和要都能达到最小，而且，延深度方向有若干个水平面，总的布置的点数较多，要使所有的点的方差和都达到最小是不可能的，当大多数的点的方差和能同时达到最小时，可以认为地下水的流速大小和方向已被获得。根据以上流程，要想使每个点的方差和最小，结合数学知识，要使方差和对地下水流速的大小u和两个方向角α和β都取一阶导数。从理论上讲，对同一个点而言，三个一阶导数同时为零，但由于实际计算以及实验的误差，一阶导数为零的可能性极小，可以设定一个较小的值，如果三个一阶导数都同时位于较小的值时，可以认为一阶导数近似为零，此时，对于该点的方差和已达到最小。公式(9)针对这些列出了相应的表达式。-0.05≤∂S∂u≤0.05-0.05≤∂S∂α≤0.05-0.05≤∂S∂β≤0.05---(9)]]>上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。当前第1页1 2 3