针对贝叶斯网络中引入专家评价的先验概率评估方法与流程

本发明属于故障诊断领域，具体涉及一种针对贝叶斯网络中引入专家评价的先验概率评估方法。
背景技术：
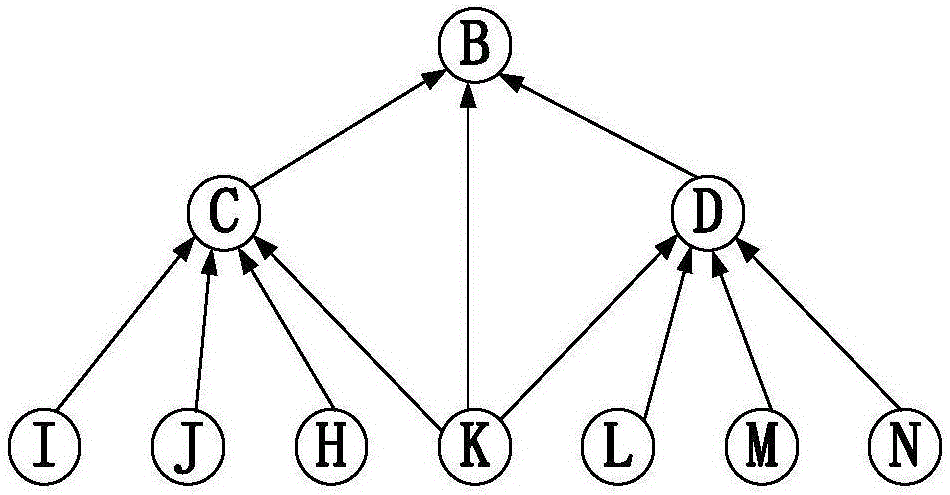
：贝叶斯网络作为故障诊断系统中常见的推理算法，网络根节点先验概率的准确程度直接决定着其能否快速定位第一故障点。然而，当统计先验概率的样本有限时，以统计概率替代先验概率的精确度就会大打折扣。较为常见的解决这种问题的做法是引入专家意见，但是引入专家意见后又会导致其他问题：如何剔除专家意见中的误差、如何融合专家组意见等。实际上，专家对先验概率进行评价时，能够凭借自身的诊断经验给出各故障事件的可能发生程度排序，但并不能给出具体的数值概率。近年来，有学者提出一种先验概率和似然函数未知时的分布式检测融合方法，然而此种方法并不适用于引入专家评价的先验概率求解。因此，发明一种针对贝叶斯网络中引入专家评价的先验概率，实现专家评价量化，结合已知的统计概率，得到较为精确的先验概率集合，最大程度提高贝叶斯网络故障诊断可靠性的评估方法具有重要意义。经对现有技术检索发现，公开文件“基于超级贝叶斯方法的专家意见先验概率修正研究”(统计与决策，2013)提出的一种修正专家意见先验概率的方法，该文件公开自述为：“针对传统贝叶斯网络方法在先验概率设定中的不足，文章提出采用超级贝叶斯方法，通过对每个专家意见赋予不同的权重，帮助决策者修正初始判断，得到更为准确的贝叶斯网络先验概率”。其不足之处是，并没有提及如何得到量化的专家评价先验概率，且当故障诊断样本容量不足时还会造成故障因子的统计先验概率缺失，尚不能解决如何获取完整的先验概率集的问题。技术实现要素：本发明的目的是提供一种针对贝叶斯网络中引入专家评价的先验概率评估方法，用以处理专家评价的误差、专家组评价的拟合，并且补全由于诊断样本不足造成的统计概率缺失，以此来获取量化的完整先验概率集。为达到上述目的，本发明包括以下步骤：步骤1，对专家评价进行误差判别，具体为：1.1，制定定性评价规则，专家们依照定性评价规则对贝叶斯网络中各故障因子的先验概率给出定性评价，并根据定性评价规则划分的等级取相应等级对应的评分值，得到的结果记为从而得到专家i对故障因子j的评价矩阵i表示第i个专家，j为对应故障因子序号，k为评价次数，k≥3；1.2，判定专家的评价失真误差。用贝塞尔公式计算标准差：其中，f表示专家第f次评价，f≤k；vf表示专家i对故障因子j的第f次评价残差，表示专家i对故障因子j的k次评价的平均值；此时利用阿贝-赫枚特判别法，对残差vf做统计量：u＝|v1v2+v2v3+…+vk-1vk|当时，则怀疑专家i对此故障因子j的评价存在失真误差；1.3，判定专家的评价经验误差。首先将每个不存在评价失真误差的专家评价结果汇总，专家i对故障因子j的k次评价去除失真误差后，取平均值aij作为对故障因子j的评分，得评分矩阵根据肖维勒准则，计算不同专家对同一故障因子j的评价残差表示故障因子j的各专家评价值的平均值，若aij的残差|vj|>Zcσ，则此数据为异常数据；Zc表示肖维勒系数，可由查表获取，σ表示对于同一故障因子j各专家给出评价值的评价标准差。步骤2，对于故障因子j，利用算术平均值和分批估计理论进行数据融合，由于专家库评价样本不大，将剔除误差后的各个专家评价数据分成两批处理；具体为：对分批后的两组数据分别求算术平均值T(1),T(2)，标准差σ(1),σ(2)，得到故障因子j的专家评价融合值为：步骤3，基于多重插补对故障因子的历史统计概率补全，具体为：3.1，将故障因子按照专家融合评价的发生等级排序后，基于多重插补采用最近距离法为故障因子历史统计概率数据集中的n个缺失概率进行插补n次，每次插补采用与缺失概率的故障因子发生等级相邻的两个故障因子的统计概率作为初始插补概率，因此可以得到2n个完整数据集。3.2，采用比估计公式确定补全后数据集的比估计量；3.3，将分析得到的数据进行合并，得到缺失概率的多重插补估计概率，从而补全历史统计概率；步骤4，对专家评价数据集和统计概率数据集进行幂函数拟合，将专家评价转化为量化的先验概率。与现有技术相比，本发明的有益效果是：本发明有效地将专家们的评价误差剔除、将专家组的评价拟合，并实现精确量化专家评价，与诊断样本得到的统计概率结合，得到了完备的先验概率集，可减小先验概率误差，以此来提高贝叶斯网络推理的准确度。附图说明图1为本发明的流程图；图2为本发明实施例中的贝叶斯网络结构示意图；图3为本发明实施例中的先验概率最终拟合效果图。具体实施方式下面结合附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。如图1所示，针对贝叶斯网络中引入专家评价的先验概率评估方法，包括以下步骤：第一步，对专家评价进行误差判别，具体为：步骤1.1，制定定性评价规则，专家们依照评价规则对贝叶斯网络中各故障因子的先验概率给出定性评价，并根据定性评价规则划分的等级取相应等级对应的评分值，得到的结果记为从而得到专家i对故障因子j的评价矩阵i表示第i个专家，j为对应故障因子序号，k为评价次数，k≥3；如图2所示，在桥式起重机制动器故障的贝叶斯网络结构里，故障因子代表的根节点分别是主弹簧I、行程制动电磁铁J、液压推动器H、制动瓦衬K、电磁铁拉力L、制动螺杆M和电磁铁线圈N；B为制动器，C为制动器刹车，D为制动器开合；定性评价规则如表1所示，一级表示发生程度最频繁(即最可能导致故障事件)，依级递减。表1故障发生概率等级对应评价规则表共邀请四位专家依照表1所示的定性评价规则对各故障因子进行故障可能性程度评价，所得结果如表2所示。表2专家分次定性评价记录表步骤1.2，判定专家的评价失真误差。首先用贝塞尔公式(1)计算标准差：其中，f表示专家第f次评价，f≤k；vf表示专家i对故障因子j的第f次评价残差，表示专家i对故障因子j的k次评价的平均值；此时利用阿贝-赫枚特判别公式(2)，对残差vi做统计量：u＝|v1v2+v2v3+…+vk-1vk|(2)当时，则怀疑专家i对此故障因子j的评价存在失真误差；对表2中的专家评价记录用公式(1)和公式(2)检验各专家对各底事件的评价失真误差，以制动瓦衬为例，所得结果如表3所示。表3制动瓦衬评价失真误差检测记录表专家1专家2专家3专家4贝赛尔公式(s)01.360.520.52残差统计量(u)04.110.780.44u>s√(k-1)否是否否评价结果正常可疑正常正常步骤1.3，判定专家的评价经验误差，首先将每个不存在评价失真误差的专家评价结果汇总，专家i对故障因子j的k次评价去除失真误差后，取平均值aij作为对故障因子j的评分，得评分矩阵根据肖维勒准则，计算不同专家对同一故障因子j的评价残差表示故障因子j的各专家评价值的平均值，若aij的残差|vj|>Zcσ，则此数据为异常数据；专家i对同一故障因子j的评价次数N1对应的肖维勒系数Zc可查表4(肖维勒系数表)获取；σ表示对于同一故障因子j不同专家给出评价集的标准差。表4肖维勒系数表N1ZcN1ZcN1ZcN1Zc31.3861.7391.92122.0341.5371.80101.96132.0751.6481.86112.00142.10经检验，专家组中可能存在的评价经验误差如表5所示。表5专家组评价经验误差鉴定结果表第二步，专家组内各个专家评价拟合，具体为：利用算术平均值和分批估计理论进行数据融合，由于专家库评价样本不大，分成2批处理基本可满足要求；对分批后的每组数据求算术平均值T(1),T(2)，标准差σ(1),σ(2)，利用公式(3)得到融合值；计算结果如表6所示：表6专家组融合意见表第三步，基于多重插补法对先验概率补全，具体为：步骤3.1，首先对250t-20m规格的桥式起重机采集的故障样本进行统计，得到故障因子的历史统计概率如表7所示：表7故障因子历史统计概率表可见，主弹簧故障概率在统计的样本中并没有出现，即出现历史统计概率缺失情况。将故障因子按照专家融合评价的发生等级排序后，基于多重插补采用最近距离法对缺失数据进行插补，即以主弹簧发生等级相邻的两个故障因子的统计概率作为初始插补概率，因此可以得到两个完整数据集，插补结果如表8所示；表8故障因子缺失历史统计概率插补步骤3.2，根据比估计公式确定补全的数据集R中的比估计量如公式(4)：yj表示故障因子j的历史统计概率，Pj表示故障因子j的专家组融合意见，表示各故障因子的专家组融合意见均值，包含和R表示插补的数据集序号。步骤3.3，将分析得到的数据进行合并，得到缺失数据的多重插补估计概率，从而补全历史统计概率；分析得到的数据合并采用公式(5)，即为缺失数据的多重插补估计值，m为插补得到的数据集个数，插补的缺失概率最终可表示为：第四步，利用matlab中的cftool工具箱对专家评价数据集和补全后的统计概率数据集进行幂函数拟合，将专家评价转化为量化的先验概率。如图3所示是两种数据的拟合曲线，利用拟合曲线就可以定位出各个故障因子的先验概率。当前第1页1 2 3