一种复杂梯级水库群蓄水期优化调度方法与流程

本发明属于水库调度技术领域，特别涉及一种复杂梯级水库群蓄水期优化调度方法。

背景技术：

为了充分发挥水能资源，防治洪涝灾害，目前主要大江大河上均已建成由干支流水电站组成的复杂梯级水库群。由于这些复杂梯级水库群的兴利库容占流域径流量的比例大幅度提高，水库汛末对河道自然流量的影响日益增强，且由于同一流域水电站的汛末蓄水时间大致相同，导致了“集中蓄水”和“竞争蓄水”的问题，影响了水库的蓄满率、蓄水期发电量等等效益。因此，必须对复杂梯级水库群蓄水期进行优化管理，并合理地配置流域有限的水资源。

现有研究对水库蓄水期调度的优化主要从两方面入手：优化水库汛末蓄水时间，优化蓄水期水库调度函数或调度规则。刘心愿等^[1]提出了一种考虑综合利用要求的三峡水库提前蓄水方案，可在保障防洪安全的同时，显著提高蓄水期发电效益与水资源利用率。李雨等^[2]建立了三峡水库提前蓄水的防洪风险与效益分析模型，以防洪风险和蓄水效益作为方案的评价指标，对汛末蓄水调度进行了优化。杨光等^[3]通过将PA-DDS算法引入水库多目标优化调度中，对其应用效果进行了评价，结果表明该算法较常用的NSGA-II与MOPSO均更优，可获得高质量的优化调度图非劣解集。周研来等^[4]对溪洛渡-向家坝-三峡梯级税局拟定了若干组同步蓄水方案和异步蓄水方案，在不降低原防洪标准的前提下，同步蓄水方案发电效益较优，异步蓄水方案的蓄水效益较优，两类方案均优于原设计方案。陈璐等^[5]基于Copula理论，对长江上游干支流洪水开展遭遇分析，通过构建干支流控制站的年最大洪水发生时间和量级的联合分布，计算洪水发生时间和量级的遭遇概率，为梯级联合调度提供参考。

梯级水库群具有防洪、发电、航运、供水、生态等综合效益，且各目标之间可能存在矛盾，如为保证蓄满率而提前蓄水可能会增大防洪风险，为保障发电用水可能会破坏生态用水等，因此如何科学、协调各目标是实现复杂梯级水库群蓄水期优化调度的关键。与单库优化或串联水库优化相较，复杂梯级水库群呈现出更高的计算复杂度，其“维数灾”问题需要得到解决。

由于复杂梯级水库群的优化计算具有高维度、高度非线性的特征，优化求解较为困难。现有研究多集中于单库优化或相对简单的串联水库群，常常仅优化水库出流过程，并未考虑对各水库的蓄水时间和蓄水控制线进行优化；对流域水库的综合利用效益考虑不充分。

文中涉及的参考文献如下：

[1]刘心愿，郭生练，刘攀，等.考虑综合利用要求的三峡水库提前蓄水方案[J].水科学进展,2009,20(6):851-856.

[2]李雨，郭生练，刘攀，等.三峡水库提前蓄水的防洪风险与效益分析[J].长江科学院院报，2013,30(1):8-14.

[3]杨光，郭生练，刘攀，等.PA-DDS算法在水库多目标优化调度中的应用[J].水利学报，2016，47(6):789-797.

[4]周研来，郭生练，陈进.溪洛渡-向家坝-三峡梯级水库联合蓄水方案与多目标决策研究[J].水利学报，2015，46(10):1135-1144.

[5]陈璐，郭生练，张洪刚，等.长江上游干支流洪水遭遇分析[J].水科学进展，2011，22(3):323-330.

技术实现要素：

针对现有技术存在的不足，本发明提供了一种复杂梯级水库群蓄水期优化调度方法。

为解决上述技术问题，本发明采用如下的技术方案：

一种复杂梯级水库群蓄水期优化调度方法，包括以下步骤：

S1收集流域基础信息，所述的流域基础信息包括水库特征参数、现有蓄水期调度规则、流域地形地貌信息、水雨情和防洪要求；

S2将复杂梯级水库群划分为若干个子流域分区，采用汛期分期法分别计算子流域分区中各水库的后汛期开始时间，各水库的后汛期开始时间构成子流域分区的后汛期开始时间；

S3对各子流域分区分别开展洪水遭遇分析，估算各子流域分区内干支流防洪节点超过安全流量的概率，并利用该概率论证汛末蓄水调度优化的可行性；

S4以复杂梯级水库群的防洪目标、发电目标、蓄水目标、航运目标和生态目标为目标函数，构建多目标蓄水调度优化模型；

S5以实测的长序列径流资料作为输入，以各水库的起蓄时间T_i、蓄水控制线Z_refill,i(t)和汛末防洪控制水位Z_flood,i为待优化变量，采用Pareto动态维度搜索法求解多目标蓄水调度优化模型，推求最优参数解，根据最优参数解获得复杂梯级水库群汛末蓄水期的确定性优化调度结果；

S6基于确定性优化调度结果，采用大系统聚合分解模型，提取汛末蓄水期的优化调度规则；

S7将流域设计洪水作为输入，对步骤S6所得优化调度规则进行防洪安全检验。

进一步的，汛期分期法为统计相关法、成因分析法、变点分析法或聚类分析法。

步骤S3具体为：

对各子流域分区分别执行如下步骤：

3.1将洪水发生时间的边缘分布转化为弧度x；

3.2采用混合von Mises分布拟合弧度x的概率密度函数f(x)；

3.3采用P-III分布拟合年最大洪水y的概率密度函数f(y)；

3.4基于概率密度函数f(x)和f(y)构建x和y的Copula联合分布函数；

3.5采用Copula联合分布函数估算干支流防洪节点超过安全流量的概率。

步骤S5具体为：

5.1随机生成满足多目标蓄水调度优化模型约束条件的初始解向量S₀＝[s₁,…,s_D]，其维度为D；重复生成N个初始解向量S₀构成初始种群S₀，一个初始解向量S₀为一组可行解；

5.2计算当前可行解对应的各项目标函数值F(S₀)，将当前可行解作为当前最优解S_best；

5.3计算当前最优解S_best中各决策变量发生变化的概率，根据概率值从当前最优解S_best的D个维度中随机选取D'个维度，随机生成D'个服从[0-1]均匀分布的随机数，若对应的概率P_d大于对应的随机数，则将相应维度加入邻域{Ξ}；其中，决策变量为水库在各计算时段的出库平均流量和蓄水控制线；

5.4在邻域{Ξ}的D'个维度中对当前最优解S_best加入扰动，得到新解S_new；

5.5计算新解S_new对应的各项目标函数值F(S_new)，若F(S_new)＞F(S_best)，用新解S_new更新当前最优解；否则，保持当前最优解不变；

5.6判断迭代数是否达到预设的最大迭代数，若达到，结束，当前最优解和当前最优解对应的各项目标函数值即最终的最优参数解和最优函数值，根据最优参数解获得确定性优化调度结果；否则，返回步骤5.3。

步骤S6具体为：

在步骤5所得各非劣解下分别进行，所述的非劣解即最优参数解：

6.1将各子流域分区分别视为一等效水库；

6.2计算各水库各计算时段t的入能r_i(t)与蓄能x_i(t)；

6.3计算各等效水库各计算时段t的总蓄能和总入能；

6.4取各等效水库的总入能、总蓄能及总入能和总蓄能的交互项作为解释变量，构建等效水库时段总出力与水库群总出力的关系；

6.5将等效水库时段总出力分配到等效水库中各水库；

6.6根据各水库分配到的出力计算各水库在各计算时段的出流量模拟值，从而获得复杂梯级水库群汛末蓄水期的优化调度规则。

复杂梯级水库群具有防洪、发电、航运、供水、生态等综合效益，然而随着水库群的兴利库容占流域径流量的比例大幅度提高，水库汛末对河道自然流量的影响日益增强，且由于同一流域水电站的汛末蓄水时间大致相同，导致了“集中蓄水”和“竞争蓄水”的问题，影响了水库的蓄满率、蓄水期发电量等效益，导致各项效益之间出现了矛盾。目前蓄水期优化调度局限于单库或串联水库，且未对汛末蓄水期调度规则进行优化，无法获得考虑复杂梯级水库整体协调作用的最优解。

本发明通过构建复杂梯级水库汛末蓄水期的多目标蓄水调度优化模型，采用Pareto动态维度搜索法模型进行寻优，基于大系统聚合分解模型提取优化调度规则，并对结果进行防洪安全检验，在不降低流域防洪标准的前提下，为复杂梯级水库汛末蓄水期优化调度提供了一种新的合理可行的方法。

本发明耦合Pareto动态维度搜索法和大系统聚合分解模型，可克服“维数灾”问题，实现对复杂梯级水库群各水库的整体联合优化；并在保障流域防洪安全的前提下，充分考虑流域各效益，实现蓄水期的综合效益最大化，得到各水库的蓄水时机及控制线，并提取得到优化调度规则。

附图说明

图1为本发明的具体流程图；

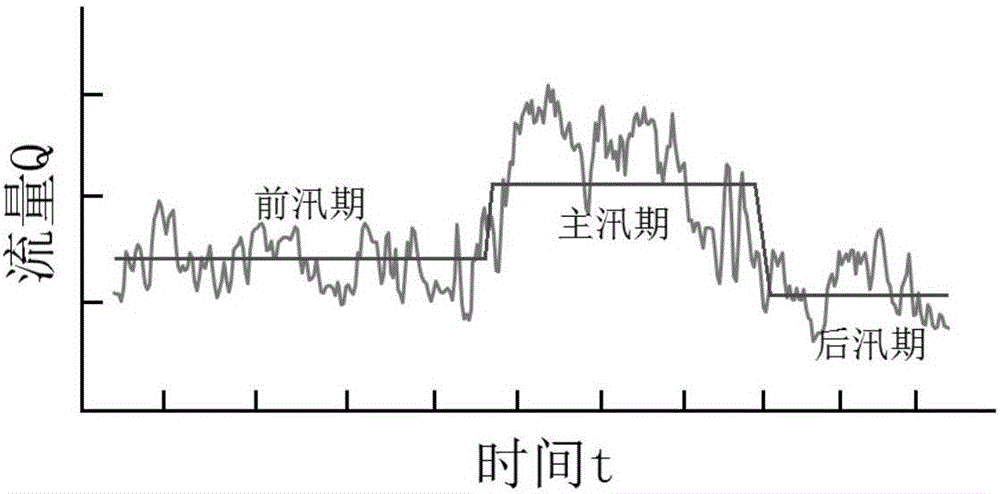
图2为实施例的汛期分期结果示意图；

图3为复杂梯级水库群的示意图；

图4为蓄水期调度控制线示意图；

图5为Pareto动态维度搜索法的具体流程图；

图6为实施例中采用Pareto动态维度搜索得到的两目标非劣解集示意图。

具体实施方式

下面将结合附图，对本发明技术方案做进一步说明。

本发明的具体流程见图1，包括如下步骤：

步骤1，收集流域基础信息，所述的流域基础信息包括水库特征参数、现有蓄水期调度规则、流域地形地貌信息、水雨情和防洪要求。

步骤2，将复杂梯级水库群划分为若干个子流域分区，采用汛期分期法计算各子流域分区的后汛期开始时间。

汛期分期法有统计相关法、成因分析法、变点分析法、聚类分析法等，本具体实施方式中采用适应性广、结果较为合理的均值变点分析法对具有防洪任务的水库进行汛期分期检验，以获得后汛期开始时间。

为便于理解，下面将对采用变点分析法进行汛期分期的具体实施过程进行详细说明。

令X＝[x₁,x₂,…,x_T]表示干支流控制站的汛期多年日均流量序列，假定其服从正态分布。

(1)假定变点数q，q一般取1或2，分别对应两期和三期。以q＝2为例，令T表示汛期时段总数，令m₁、m₂分别表示两个分期点在汛期的位置，取符合条件1＜m₁＜m₂＜n的所有(m₁,m₂)组合。

(2)对各组(m₁,m₂)，按式(1)分别计算其统计量S：

式(1)中，t表示汛期时段，x_t表示汛期时段t的日均流量。

(3)统计量S最小的一组(m₁,m₂)即最终的分期点，即汛期的第m2+1～n天为后汛期。图2为本实施例的汛期分期结果示意图。

对各水库分别重复子步骤(1)～(3)，得子流域分区的后汛期开始的时间M₂：

M₂＝(m₂(1),m₂(2),…,m₂(k))+1 (2)

式(2)中，k表示子流域分区内的水库数，m₂(1)、m₂(2)......m₂(k)分别表示第1、2……k个水库的后汛期开始时间。

对于各水库而言，进行优化搜索时，其起始蓄水时间不得早于本步骤所确定的时间M₂。

步骤3，对各子流域分区分别开展洪水遭遇分析，估算各子流域分区内干支流防洪节点超过安全流量的概率。

通过对流域开展洪水遭遇分析，可估计干支流洪水发生时间和量级遭遇的可能和概率，进而估算防洪节点处设计安全流量的发生概率。干支流洪水的遭遇问题可认为服从多变量联合分布，采用Copula函数进行描述。

对各子流域分区的控制站流量过程进行分析。首先，将洪水发生时间的边缘分布转化为弧度，采用混合von Mises分布进行描述；然后，估计年最大洪水的P-III分布参数；最后，采用Copula函数建立洪水发生时间与量级的联合分布。

(1)将洪水发生时间的边缘分布转化为弧度x：

x＝2π·D_j/L (3)

式(3)中：D_j表示第j年的洪水发生时间；L为汛期长度。

(2)用混合von Mises分布拟合弧度x的概率密度函数f(x)：

式(4)中：c表示混合von Mises分布的组成部分编号，m表示组成部分数量；p_c为组成部分c的混合比例；μ_c表示组成部分c的位置参数；κ_c表示组成部分c的尺度参数；I₀(κ_c)为第一类0阶修正的Bessel函数。

以上参数均可采用拟牛顿法估计得到。

(3)用P-III分布拟合年最大洪水y的概率密度函数f(y)：

式(5)中：α、β、δ分别表示P-III分布的形状参数、尺度参数和位置参数，α＞0，β＞0，δ≤y＜∞，α、β、δ可采用线性矩法估计参数；Γ(·)表示伽马函数。

(4)构建洪水发生时间x和量级y的Copula联合分布函数F_X,Y(x,y)：

F_X,Y(x,y)＝C(F(x),F(y)) (6)

式(6)中：C(·)表示Copula函数；F(x)与F(y)分别为x和y的概率分布函数，可由f(x)、f(y)积分获得。

根据得到的Copula联合分布函数F_X,Y(x,y)，推测同一时间，防洪节点上的干支流遭遇洪水超过设计安全流量的概率，将其与原设计频率对比，可论证汛末蓄水调度优化的可行性。

步骤4，以防洪目标、发电目标、蓄水目标、航运目标和生态目标为目标函数，构建复杂梯级水库群的多目标蓄水调度优化模型，其中，防洪目标以约束条件形式实现。

复杂梯级水库群示意图见图3。多目标蓄水调度优化模型的待优化变量为各水库汛末蓄水期调度图，见图4，具体为各水库的起蓄时间T_i、蓄水控制线Z_refill,i(t)和汛末防洪控制水位Z_flood,i。

各优化目标函数如下：

(1)发电目标为计算时段水库群总发电量最大，发电目标函数如下：

N_i(t)＝K_iQ_i(t)H_i(t) (8)

式(7)～(8)中：E为计算时段水库群的总发电量；T为计算时段数量，t为计算时段序号，Δt为计算时段步长；n为梯级水库群的水库数，i为水库序号；N_i(t)为水库i在计算时段t的出力；K_i为水库i的出力系数；Q_i(t)为水库i在计算时段t的发电流量；H_i(t)为水库i在计算时段t的平均发电水头。

(2)蓄水目标包括水库群的蓄满率最大和弃水量最小，蓄水目标函数如下：

式(9)～(10)中：R_f为水库的蓄满率；Z_end(i)表示蓄水期末水库i的水位；Z_max(i)表示水库i的正常蓄水位；#(·)为指示函数，满足条件则取值1，否则取值0；Q_w为水库的弃水量；Q_W,i(t)表示水库i在计算时段t的弃水量。

(3)航运目标为通航率最大，航运目标函数如下：

式(11)中：R_nav为通航率；Q_out,i(t)表示水库i在计算时段t的出库平均流量；Q_ship,i表示水库i的最小通航流量。

(4)生态目标为生态流量保证率最大，生态目标函数如下：

式(12)中：R_eco为生态流量保证率；Q_out,i(t)表示水库i在计算时段t的出库平均流量；Q_eco,i表示水库i的最小生态流量。

各约束条件如下：

(1)水量平衡约束条件：

V_i(t)＝V_i(t-1)+(Q_in,i(t)-Qo_ut,i(t))·Δt-W_i(t) (13)

式(13)中：V_i(t)和V_i(t-1)分别表示水库i在计算时段t和t-1的库容；Q_in,i(t)和Q_out,i(t)分别表示水库i在计算时段t的入库平均流量和出库平均流量；Δt表示计算时间步长；W_i(t)表示水库i在计算时段t的水分损失量，如蒸散发、渗漏等。

(2)水位约束条件：

Z_min,i(t)≤Z_i(t)≤Z_max,i(t) (14)

式(14)中：Z_i(t)表示水库i在计算时段t的水位；Z_max,i(t)和Z_min,i(t)分别表示水库i在计算时段t的允许最高水位和允许最低水位。

当计算时段t未发生洪水时，若Z_i(t)＜Z_reflii,i(t)，则降低出力发电；当计算时段t末未发生洪水时，控制Z_refill,i(t)≤Z_i(t)≤Z_flood,i(t)，并相应出力；当发生蓄水期校核洪水时，控制Z_i(t)≤Z_jh,i，Z_jh,i为水库i的校核水位。

(3)出力约束条件：

P_min,i(t)≤P_i(t)≤P_max,i(t) (15)

式(15)中：P_i(t)表示水库i在计算时段t的出力；P_max,i(t)和P_min,i(t)分别表示水库i在计算时段t的允许最大出力和允许最小出力。

(4)防洪约束条件，即出库流量约束条件：

Q_out,i(t)≤Q_s,i(t) (16)

式(16)中：Q_s,i(t)表示水库i在计算时段t的安全泄量，Q_out,i(t)表示水库i在计算时段t的出库平均流量。

(5)地质防灾约束条件：

|Q_out,i(t)-Q_out,i(t-1)|≤ΔQ (17)

式(17)中：ΔQ表示泄流变化量的允许值；Q_out,i(t)和Q_out,i(t-1)分别表示水库i在计算时段t、t-1的出库平均流量。

(6)河道演算约束条件：

Q_in,i+1(t)＝C₀(i-1,i)Q_out,i(t)+C₁(i-1,i)Q_out,i(t-τ)+C₂(i-1,i)Q_in,i+1(t-τ)+Q_qj,i-1(t) (18)

式(18)中：Q_in,i+1(t)表示水库i+1在计算时段t的入库平均流量；C₀(i-1,i)、C₁(i-1,i)和C₂(i-1,i)分别为水库i、i+1间演算的马斯京根参数；Q_out,i(t)表示水库i在计算时段t的出库平均流量；Q_out,i(t-τ)表示水库i在计算时段t-τ的出库平均流量，τ为水流传播滞时；Q_in,i+1(t-τ)表示水库i+1在计算时段t-τ的入库平均流量；Q_qj,i-1(t)表示水库i在计算时段t的区间径流量。Q_out,i(t)和Q_out,i(t-τ)采用水库i的上游水库的出库流量观测值或上游水文站的流量观测值。

(7)非负约束条件：

Λ≥0 (19)

式(19)中：Λ表示以上各优化目标函数及约束条件中各项变量。

步骤5，以实测的长序列径流资料作为输入，求解多目标蓄水调度优化模型，推求复杂梯级水库群汛末蓄水期的确定性优化调度结果。

由于多目标蓄水调度优化模型属于非线性、高维度、多目标的优化问题，常规算法很难获得全局最优解，本发明采用Pareto动态维度搜索法求解多目标蓄水调度优化模型，其流程见图5，具体步骤如下：

(1)随机生成满足多目标蓄水调度优化模型约束条件的初始解向量S₀＝[s₁,…,s_D]，其维度为D，给定各维度的上限S_max和下限S_min，上限S_max和下限S_min根据多目标蓄水调度优化模型的约束条件给定。

重复生成N个初始解向量S₀构成初始种群，记为S0，S0的每一行为一组可行解，即一个初始解向量S₀为一组可行解。

本发明中，S₀＝[{V_i(t)},{Z_refill,i(t)},{Z_flood,i},{Q_out,i(t)}]，V_i(t)表示水库i在计算时段t的库容，Z_refill,i(t)表示水库i在计算时段t的蓄水控制线，Z_flood,i表示水库i的汛末防洪控制水位，Q_out,i(t)表示水库i在计算时段t的出库平均流量；i＝1,2,…,n，n为梯级水库群的水库数。

(2)计算当前可行解对应的各项目标函数值F(S₀)，并将当前可行解作为当前最优解S_best。

(3)计算当前最优解中各决策变量发生变化的概率P_d＝1-ln(d)/ln(m)，即第d个维度加入邻域{Ξ}的概率为P_d，其中m为预设的最大迭代数，d＝1,2,...D。根据概率P_d值从当前最优解的D个维度中随机选取D'个维度，并随机生成D'个服从[0-1]均匀分布的随机数，若对应的概率P_d大于对应的随机数，则将相应维度加入邻域{Ξ}。若某次随机选取过程没有维度加入{Ξ}，则任意选取一个维度加入{Ξ}中。本发明中，决策变量为水库在各计算时段的出库平均流量和蓄水控制线。

(4)在邻域{Ξ}的D'个维度中对当前最优解S_best加入扰动，得到新解S_new。

扰动方式如下式：

式(20)～(21)中：N(0,1)表示服从标准正态分布的随机数；j表示维度编号，j＝1，2，……，D'；σ_j为第j个维度的扰动标准差，由式(21)计算得到；表示第j个维度的当前最优解；表示扰动后的新值；r表示前文中的扰动参数；和分别表示第j个维度的最大值和最小值。

(5)计算新解S_new对应的各项目标函数值F(S_new)，若F(S_new)＞F(S_best)，即新解的所有目标函数值均大于S_best的目标函数值，用新解S_new更新当前最优解；否则，保持当前最优解不变。

(6)判断迭代数是否达到预设的最大迭代数，若达到，结束，当前最优解和当前最优解对应的各项目标函数值即最终的最优参数解和最优函数值；否则，返回步骤(3)。

根据最优参数解可获取确定性优化调度结果，所述的确定性优化调度结果即水库最优出流过程与蓄水过程。

由于Pareto动态维度搜索属于一种进化式并行智能算法，可同时选取多个初始解向量进行并行搜索，从而得到多目标优化的Pareto前沿(非劣解集)。Pareto动态维度搜索计算得到的两目标非劣解集示意图见图6。

步骤6，在确定性优化调度结果下，采用大系统聚合分解模型，提取汛末蓄水期的优化调度规则。

将步骤2划分所得的K个子流域分区分别视为一等效水库。

具体通过以下子步骤实现：

(1)计算各水库在计算时段t的入能r_i(t)与蓄能x_i(t)。

式(22)～(23)中：r_i(t)表示水库i在计算时段t的入能，x_i(t)表示水库i在计算时段t的蓄能；k_i表示水库i的出力系数；表示水库i在计算时段t的平均发电水头；V_min,i(t)表示水库i在计算时段t的最小库容；H_i(V)表示水库i的库容～发电水头函数。

(2)计算各等效水库在计算时段t的总入能和总蓄能

对于并联水库，可直接将其入能和蓄能相加作为总入能和总蓄能。

两个并联水库的总入能为：

两个并联水库的总蓄能为：

式(24)～(25)中：r_i+1(t)、x_i+1(t)分别表示水库i+1在计算时段t+1的入能与蓄能；k_i+1表示水库i+1的出力系数；表示水库i+1在计算时段t的平均发电水头；V_min,i+1(t)表示水库i+1在计算时段t的最小库容；H_i+1(V)表示水库i+1的库容～发电水头函数。

对于串联水库，需要考虑上游水库下泄的流量重复利用的问题，分别按照式(24)和式(25)计算总入能和总蓄能：

式(26)～(27)中：ΔV_i(t)表示水库i在计算时段t的可用库容。

对于混联水库，可将其依照串联水库和并联水库的公式逐步合成。

将各等效水库的总入能和总蓄能分布分别记为R_k(t)与X_k(t)，k＝1,2,…,K。

(3)建立等效水库时段总出力与复杂水库群总出力的关系，此处取总入能、总蓄能及其交互项作为解释变量：

P_k(t)＝F_dx,k(R_k(t),X_k(t),R_k(t)·X_k(t))＝a₁·R_k(t)+b₁·X_k(t)+c₁·R_k(t)·X_k(t)+d₁ (28)

式(28)中：P_k(t)表示第k个等效水库在计算时段t的出力；F_dx,k表示函数符号；a₁、b₁、c₁、d₁均为待定参数。

(4)将等效水库时段总出力分配到各水库：

p_i(t)＝F_res,i(r_i(t),x_i(t),r_i(t)·x_i(t))＝a₂·r_i(t)+b₂·x_i(t)+c₂·r_i(t)·x_i(t)+d₂ (29)

式(29)中：p_i(t)表示第i个水库在计算时段t的出力；F_res,i表示函数符号；a₂、b₂、c₂、d₂均为待定参数。

(5)计算水库i在计算时段t的出流量模拟值Q_out,i(t)：

对步骤5中得到的非劣解集中各非劣解集进行上述大系统聚合分解计算，可得到复杂梯级水库群汛末蓄水期的优化调度规则的非劣解集。所述的非劣解集即步骤5获得的最终的最优参数解。

对计算时段t的各水库出流决策，只需要知道计算时段t初各水库的状态，即可求得水库群总出力，进而通过式(28)～(30)来获得计算时段的优化出流过程。

步骤7，将流域设计洪水作为输入，对步骤6所获得的优化调度规则进行防洪安全检验。

采用不同典型年的设计洪水与校核洪水进行防洪安全检验，将其中通过防洪安全检验的优化调度规则保留下来，剔除无法满足流域防洪安全的优化调度规则。