一种支撑点集合的选择方法及装置与流程

本发明属于计算机领域，尤其涉及一种支撑点集合的选择方法及装置。

背景技术：

大数据的4V特性中关于Variety(类型)的探索相对较少。数据的多样性，泛指类型(文本、图像、音频、视频、空间数据、时空序列等)和来源(媒体、教育、经济、医疗、航天等)的广泛。处理种类繁多的数据一般有采用专用系统或通用系统两种方式。专用系统为每种数据类型量身定做专门的处理系统，因此需要开发多个处理系统，性能较好但开发维护成本高，适用范围窄。通用系统开发一个统一的系统来处理多种数据类型的数据，性能相对专用系统可能较差，但具有较低的开发维护成本和较宽广的适用范围。如果性能满足应用需求，则具有很高的性价比，因而往往成为商业软件的选择。

当前，大数据应用领域急需通用的功能强大且易于使用和维护的数据分析管理系统。构建通用的数据管理分析系统的基本途径是首先把多种数据按照其共性抽象到统一的数据类型和统一的匹配衡量方法，然后针对统一的数据类型和匹配衡量方法设计数据分析管理框架。

度量空间(Metric space)是一种覆盖范围很广的数据类型的抽象。它只要求定义满足度量空间性质的距离函数，而距离函数的具体实现和数据表达都是透明的，同样的算法可以应用于不同的数据，因而具备了更广泛的适用范围。度量空间最大的优势在于其高度的普遍适用性。用户只需提供距离函数就可以进行相似性搜索。然而，度量空间的优势也是其劣势。数据被抽象成度量空间中的点，虽然提高了通用性，但同时也损失了坐标信息，唯一可用的信息就是距离值。由于没有坐标，许多数学工具不能直接使用。为此，通常的方法是先找出一些参考点(也称支撑点，Pivot)，然后将数据到此参考点的距离作为坐标。支撑点的好坏对于度量空间数据管理分析的性能发挥着关键性的影响。

Incremental算法(递增算法)是一种增量式(一个一个地选出)选择支撑点的方法。该算法需要一个候选集和一个评价集，以及一个用于衡量支撑点好坏的目标函数。在选定的候选集上，通过评价集来计算候选集中每个数据对应的目标函数值，选择具有最优目标函数值的数据作为支撑点。

Incremental算法虽然能够快速地选出支撑点，但也存在着落入局部最优的问题：以最优目标函数值依次选出的两个支撑点组合在一起，不一定是性能最优的支撑点组合。也就是说，在选出的第一个支撑点是最优支撑点的情况下，当选择第二个支撑点时，因为受到第一个支撑点的影响，即使是以最优目标函数值选出第二个支撑点，但两个支撑点组合在一起却不是全局最优的。

技术实现要素：

本发明所要解决的技术问题在于提供一种支撑点的选择方法及装置，旨在解决现有技术提供的Incremental算法中以最优目标函数值依次选出的两个支撑点组合在一起，不一定是性能最优的支撑点组合的问题。

本发明是这样实现的，一种支撑点集合的选择方法，包括：

接收数据集和支撑点个数，并从所述数据集中确定候选集和评价集；

根据所述候选集和所述支撑点个数得到若干支撑点集合；

将所述评价集中的数据两两组合得到数据对，以组合后的数据对构建评价数据对集合；

判断每一所述支撑点集合是否能够以预置排除规则排除所述评价数据对集合中的每一数据对，并得到每一所述支撑点集合的排除个数；

选取所述排除个数中的最大值，以所述最大值对应的支撑点集合作为选择的支撑点集合。

进一步地，所述从所述数据集中确定候选集和评价集包括：

以随机抽取、近期最远遍历中的其中一种方法从所述预置的数据集中确定所述候选集；及：

以最远最先遍历方法从所述预置的数据集中确定所述评价集。

进一步地，所述接收预置的数据集和支撑点个数之后，还包括：

接收索引半径；

则所述判断每一所述支撑点集合是否能够以预置排除规则排除所述评价数据对集合中的每一数据对，并得到每一所述支撑点集合的排除个数包括：

通过距离度量函数计算所述支撑点集合与所述评价数据对集合中数据对之间各数据的距离，及所述数据对中两个数据之间的距离；

判断数据间的距离是否大于所述索引半径，若满足，则获取大于所述索引半径的数据对的个数。

进一步地，以coms[i]表示第i个支撑点集合，以dataPairs[j]表示所述评价数据对集合中的第j个元素，以count[i]表示第i个支撑点集合的排除个数，则判断数据间的距离是否大于所述索引半径，若满足，则获取大于所述索引半径的数据对的个数包括：

判断第i支撑点集合coms[i]是否能够以三角形不等性排除所述评价数据对集合中的第j个元素dataPairs[j]；

若所述第i支撑点集合coms[i]将所述第j个元素dataPairs[j]排除，则增加所述排除个数count[i]；

若所述第i支撑点集合coms[i]不能将所述第j个元素dataPairs[j]排除，则保持所述排除个数count[i]不变。

进一步地，所述选取所述排除个数中的最大值，以所述最大值对应的支撑点集合作为选择的支撑点集合之后，还包括：

利用所述索引半径对所述选择的支撑点集合建立索引，并将建立索引后的所述选择的支撑点集合保存至预置存储单元中。

本发明实施例还提供了一种支撑点集合的选择装置，包括：

数据接收单元，用于接收数据集和支撑点个数，并从所述数据集中确定候选集和评价集；

集合获取单元，用于根据所述候选集和所述支撑点个数获取若干支撑点集合；

集合构建单元，用于将所述评价集中的数据两两组合得到数据对，以组合后的数据对构建评价数据对集合；

数据排除单元，用于判断每一所述支撑点集合是否能够以预置排除规则排除所述评价数据对集合中的每一数据对，并得到每一所述支撑点集合的排除个数；

集合确定单元，用于选取所述排除个数中的最大值，以所述最大值对应的支撑点集合作为选择的支撑点集合。

进一步地，所述数据接收单元具体用于：

以随机抽取、近期最远遍历中的其中一种方法从所述预置的数据集中确定所述候选集；及：

以最远最先遍历方法从所述预置的数据集中确定所述评价集。

进一步地，所述数据接收单元还用于：

接收索引半径；

则所述数据排除单元包括：

距离计算模块，用于通过距离度量函数计算所述支撑点集合与所述评价数据对集合中数据对之间各数据的距离，及所述数据对中两个数据之间的距离；

个数获取模块，用于判断数据间的距离是否大于所述索引半径，若满足，则获取大于所述索引半径的数据对的个数。

进一步地，以coms[i]表示第i个支撑点集合，以dataPairs[j]表示所述评价数据对集合中的第j个元素，以count[i]表示第i个支撑点集合的排除个数，则个数获取模块具体用于：

判断第i支撑点集合coms[i]是否能够以三角形不等性排除所述评价数据对集合中的第j个元素dataPairs[j]；

若所述第i支撑点集合coms[i]将所述第j个元素dataPairs[j]排除，则增加所述排除个数count[i]；

若所述第i支撑点集合coms[i]不能将所述第j个元素dataPairs[j]排除，则保持所述排除个数count[i]不变。

进一步地，所述选择装置还包括：

集合保存单元，用于利用所述索引半径对所述选择的支撑点集合建立索引，并将建立索引后的所述选择的支撑点集合保存至预置存储单元中。

本发明与现有技术相比，有益效果在于：本发明通过从预置的数据集中确定候选集和评价集之后，根据预置的支撑点个数和候选集获取若干支撑点集合后和从评价集中构建评价数据对集合，以每一支撑点集合排除评价数据对集合中的每一数据对，以排除个数最多的支撑点集合为最后选择的支撑点集合。本实施例在确定候选集和评价集的情况下，能够一次性选出性能最优的支撑点集合，避免了现有技术提供的Incremental算法中以最优目标函数值依次选出的两个支撑点组合在一起，不一定是性能最优的支撑点组合的问题。

附图说明

图1是本发明第一实施例提供的一种支撑点集合的选择方法的流程图。

图2是本发明第一实施例提供的支撑点集合的选择方法和Incremental算法的对比图。

图3是本发明实施例提供的一种支撑点集合的选择装置的结构示意图。

图4是本发明实施例提供的一种支撑点集合的选择装置的详细结构示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

图1示出了本发明实施例提供的一种支撑点集合的选择方法，包括：

S101，接收数据集和支撑点个数，并从所述数据集中确定候选集和评价集；

S102，根据所述候选集和所述支撑点个数得到若干支撑点集合；

S103，将所述评价集中的数据两两组合得到数据对，以组合后的数据对构建评价数据对集合；

S104，判断每一所述支撑点集合是否能够以预置排除规则排除所述评价数据对集合中的每一数据对，并得到每一所述支撑点集合的排除个数；

S105，选取所述排除个数中的最大值，以所述最大值对应的支撑点集合作为选择的支撑点集合。

下面通过具体的步骤对本实施例进行进一步地阐述：

为了解决技术背景中的问题，本发明实施例提供了一种可以处理多种数据类型的支撑点集合的选择方法。

Incremental算法是一种增量式选出支撑点的方法，即支撑点是一个一个被选出的，存在局部最优的问题。为了解决这个问题，本实施例中提出了支撑点集合的选择方法(Pivot Set Selection，PSS)。不同于Incremental算法，PSS算法是一次性选出所有支撑点的方法，这样就避免了局部最优的问题。本实施例提供的PSS算法过程如下：

算法PSS()

输入：数据集data，

距离度量函数metric，

支撑点个数numPivots，

索引半径radius

输出：支撑点集合pivotSet

本发明提供的支撑点集合的选择方法的第1步是从数据集data中构造出候选集；第2步是从构造出的候选集中组合出所有支撑点集合，比如说候选集大小为10，支撑点个数为3，那么就会有C(10，3)＝120个集合。第3步是从数据集中构造出评价集，然后将评价集中的数据两两组合构成数据对，比如说评价集大小为8，则有C(8，2)＝28个数据对。候选集和评价集的构造方法有很多，比如随机抽取，或者将采用的以近期最远遍历(Recent Farthest Traversal，RFT)构造候选集和以最远最先遍历(Farthest First Traversal，FFT)构造评价集。PSS算法的主要思路是以coms[i]为支撑点集合，判断是否能将数据对dataPairs[j]以三角不等性排除掉；如果可以排除掉，则当前排除个数count加一；最终，将具有最多排除个数的支撑点集合作为选择的支撑点集合。

PSS算法中用到了半径敏感目标函数，即以支撑点空间中数据间距离大于索引半径radius的数据对个数作为目标函数值。算法过程中的count的值就是半径敏感目标函数值。不过，本实施例对半径敏感目标函数进行了修改，将(dist0+dist1)<＝radius也考虑了进来，即查询对象到支撑点的距离dist0与支撑点到目标对象的距离dist1的和，小于等于查询半径radius。这种情况发生在radius很大的时候，查询对象与目标对象不用计算距离就可以将目标对象放入结果集。

本实施例中以候选集和评价集都是整个数据集的最坏情况来考虑PSS算法的时间复杂度。以n表示数据集大小，因为PSS算法中需要存储数据对，n个数据，两两组合，共有C(n,2)＝(n-1)*n/2个组合，所以空间复杂度为O(n^2)。至于存放所有组合的数组com和评价集中的所有数据对dataPairs，本实施例通过预置存储方式避免对组合的存储，比如在每次循环中即时生成一个组合等。

虽然PSS算法在最坏情况下的时间复杂度很高，但一般情况下，因为候选集和评价集都比较小，尤其以RFT来选择候选集、以FFT来选择评价集之后，候选集和评价集都大大减小，使得PSS算法更具适用性。另外，跟Incremental算法类似，PSS算法也可以看作是一个算法框架，因为候选集和评价集都是可变的，但目标函数必须使用半径敏感目标函数，而不能用距离和目标函数。

PSS算法不存在局部最优的问题，因为所有支撑点是一次性选出的，只要候选集和评价集足够好，选出的支撑点一定是最优的。相较于Incremental算法，PSS算法选出的支撑点集合性能更好。

输入参数metric跟数据集data是对应的距离函数，不同的数据采用的距离计算方式是不同的。因为数据被抽象到度量空间，所以距离函数需要满足度量空间的要求。度量空间可定义为一个二元组(S，d)，其中S是有限非空的数据集合，而d是定义在S上的具有如下三个性质的距离函数：

正定性：对于任意x,y∈S,d(x,y)>＝0，并且

对称性：对于任意x,y∈S,d(x,y)＝d(y,x)；

三角不等性：对于任意x,y,z∈S,d(x,y)+d(y,z)>＝d(x,z)。

所以，在度量空间中使用的距离函数，均需满足正定性、对称性和三角不等性。

输入参数radius是目标函数需要用到的索引半径，这个半径的确定是经验性的，一般是依据查询时需要的距离计算次数，通常最大半径选择为距离计算次数不超过数据量的20％时所对应的半径。

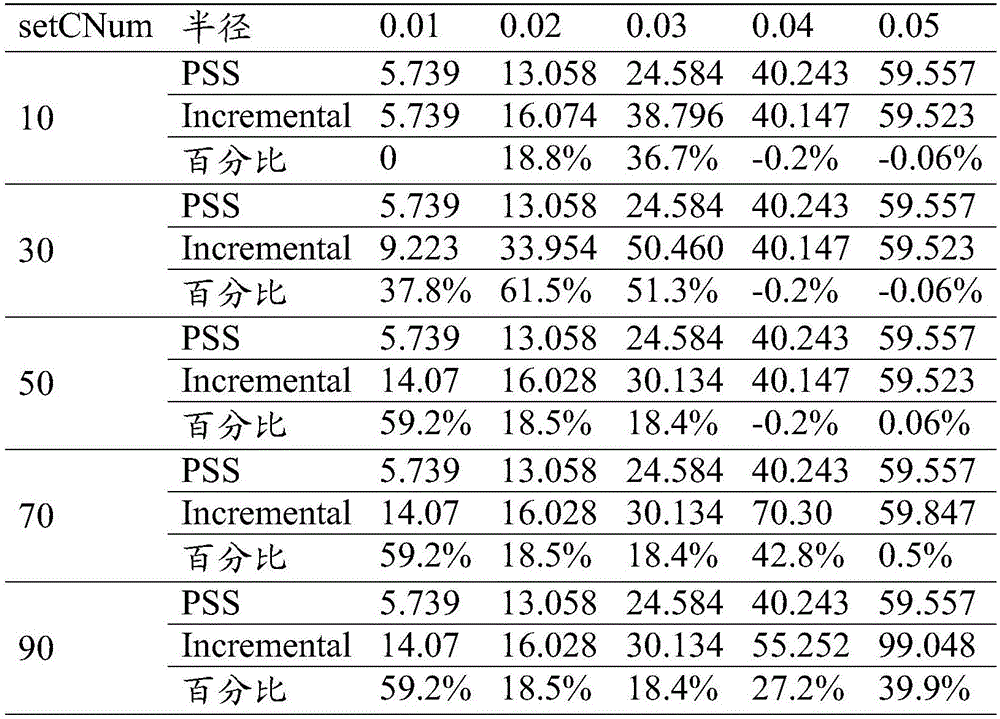
本发明实施例避免了Incremental算法的局部最优问题，在选定的候选集和评价集足够好的情况下，确保一定能够选出性能最优的支撑点集合。下面通过测试数据来展示PSS带来的有益效果。测试数据为Uniform Vector的2维数据，数据量为5000，距离函数使用欧几里得距离，索引半径为0.01～0.05，索引形式为Pivot Table，即索引建立过程中没有数据划分，查询时顺序扫描数据，通过数据到支撑点的距离来排除。分别在PSS算法和Incremental算法中，以RFT选出候选集，以FFT选出评价集，目标函数使用上面说到的修改后的半径敏感目标函数。保持评价集大小为50不变，逐渐增大候选集大小，实验结果如图2所示。

图2中，最左边一列中的10、30、50、70、90为候选集的大小N；在每个候选集上，分别以PSS和Incremental选出支撑点建立索引，在索引上查询5000个数据得到距离计算次数的平均值avgNum；百分比为PSS比Incremental性能提升的比例。从图2中可以得出以下几点：

(1)每个大小的候选集上，PSS均有比Incremental性能更高的表现。以setNum表示候选集大小，当setCNum＝30时，在半径0.02上，PSS比Incremental性能提升了61.5％；

(2)当候选集变大时，在每个半径上，Incremental都出现了性能不增反降的现象。如下：

在半径0.01上，随着setCNum从10增加到50，avgNum从5.739增加到9.223，再增加到14.07；

在半径0.02上，setCNum从10增加到30时，avgNum从16.074增加到33.954；

在半径0.03上，setCNum从10增加到30时，avgNum从38.796增加到50.460；

在半径0.04上，setCNum从50增加到70时，avgNum从40.147增加到70.30；

在半径0.05上，setCNum从70增加到90时，avgNum从59.847增加到99.048。

出现这种现象的主要原因是Incremental的局部最优问题。随着候选集的增大，第一个支撑点的选择范围变大，Incremental根据最优目标函数值选出的第一个支撑点跟最优支撑点差距变大。

(3)有些半径上，PSS比Incremental性能差一些，比如图2中百分比为负数的那些半径上。这是因为评价集不是全体数据，即使候选集包含了最优的两个支撑点，但目标函数并不能完全准确地选出它们。而且，在这些半径上，PSS比Incremental差的比例均不足1％，对性能几乎没影响。

(4)随着候选集的增大，PSS选出的支撑点的性能几乎没有变化。这说明以RFT选择候选集，可以缩小候选集的大小，从而降低了构建索引需要的代价。

(5)在候选集大小相同的情况下，虽然PSS需要距离计算次数比Incremental多，但是从图2中能够看出来，当候选集很小时(比如10)就已经具有相当不错的性能，所以相对Incremental来说，PSS可以通过减小候选集的方式来减少距离计算次数。

下面对本实施例中使用的Incremental算法、RFT算法、FFT算法及本其他参数进行进一步地解释：

1、Incremental算法

令S表示数据集，setE表示评价集，setC表示候选集，P为支撑点集合，大小为k(即要选择k个支撑点)。其中，setE是大小为A的数据对集合：

setE＝{(a₁,a₁'),(a₂,a'₂),...,(a_A,a'_A)},a_i,a_i'∈S

setC是大小为N的数据集合：

setC＝{c|c∈S}

算法过程如下：

算法Incremental()

输入：数据集data，

距离度量函数metric，

支撑点个数numPivot

输出：结果集resultSet

1)从数据集S中抽样，得到评价集setE；

2)如果支撑点个数没有选满，即i<k，进入第3)步，否则进入第10)步；

3)从S中抽样，得到候选集setC；

4)遍历setC，Cj与当前支撑点集合组合得到新的支撑点集合P’，即

P'＝{x|P∪C_j}；

5)将setE映射到P’定义的空间中；

6)使用目标函数计算setE包含的距离对的均值；

7)与setC中其他候选点比较，取均值最大值者为支撑点，即pi；

8)更新支撑点集合P，使得P＝P∪pi；

9)返回2)步；

10)算法结束。

从算法过程可以看出，如果候选集大小为N，评价集大小为M，需要选择k个支撑点，那么Incremental算法的时间复杂度为O(kMN)。因为一般评价集会远大于候选集，所以空间复杂度为O(M)。算法中，有三个地方是可以变化的：第一，候选集的选取方式；第二，评价集的选取方式；第三，目标函数。所以说，Incremental不仅是一个算法，更是一个框架——不同的候选集和评价集选取方式以及不同的目标函数均可放入其中。

2、RFT算法

近期最远遍历(Recent Farthest Traversal，RFT)，是一种选择支撑点的方法，它的特点是能够更快选出性能更优的支撑点，其中“更快”和“更优”是相对FFT算法而言的。算法主要过程如下：

算法RFT()

输入：数据集data，

距离度量函数metric，

选点个数pointNum

输出：结果集resultSet

3、FFT算法

最远优先遍历(Farthest First Traversal，FFT)可以在线性时间内选出数据拐角的点，并且性能有一定的保证，是使用最广泛的支撑点选取算法之一。它跟RFT算法很像，都能够在线性时间内选出支撑点，但选出最优点的速度不如FFT。FFT除了用来选择支撑点外，还有具有很好地抽样性能，所以在算法PSS中，使用FFT来选择评价集，具有不错的性能。FFT算法过程如下：

算法.FFT()

输入：数据集data，

距离函数metric，

选点个数pointNum

输出：结果集resultSet

本发明还提供了如图3所示的一种支撑点集合的选择装置，包括：

数据接收单元301，用于接收数据集和支撑点个数，并从所述数据集中确定候选集和评价集；

集合获取单元302，用于根据所述候选集和所述支撑点个数获取若干支撑点集合；

集合构建单元303，用于将所述评价集中的数据两两组合得到数据对，以组合后的数据对构建评价数据对集合；

数据排除单元304，用于判断每一所述支撑点集合是否能够以预置排除规则排除所述评价数据对集合中的每一数据对，并得到每一所述支撑点集合的排除个数；

集合确定单元305，用于选取所述排除个数中的最大值，以所述最大值对应的支撑点集合作为选择的支撑点集合。

进一步地，本发明还提供了如图4所示的一种支撑点集合的选择装置，包括：

数据接收单元401，用于接收数据集和支撑点个数，并从所述数据集中确定候选集和评价集；

集合获取单元402，用于根据所述候选集和所述支撑点个数获取若干支撑点集合；

集合构建单元403，用于将所述评价集中的数据两两组合得到数据对，以组合后的数据对构建评价数据对集合；

数据排除单元404，用于判断每一所述支撑点集合是否能够以预置排除规则排除所述评价数据对集合中的每一数据对，并得到每一所述支撑点集合的排除个数；

集合确定单元405，用于选取所述排除个数中的最大值，以所述最大值对应的支撑点集合作为选择的支撑点集合。

集合保存单元406，用于利用所述索引半径对所述选择的支撑点集合建立索引，并将建立索引后的所述选择的支撑点集合保存至预置存储单元中。

进一步地，数据排除单元404包括：

距离计算模块，用于通过距离度量函数计算所述支撑点集合与所述评价数据对集合中数据对之间各数据的距离，及所述数据对中两个数据之间的距离；

个数获取模块，用于判断数据间的距离是否大于所述索引半径，若满足，则获取大于所述索引半径的数据对的个数。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。