一种用于工控领域的信号获取方法与流程

本发明涉及工业控制技术领域，具体地说，涉及一种用于工控领域的信号获取方法。

背景技术：

对于高次方程的求根问题，由于数学上已证明不存在求根公式，因此采用计算机求取高次方程的根是唯一可行的方法。目前计算机求根过程中广泛使用的都是基于牛顿下山法的迭代算法，或者是多种改进的牛顿迭代算法。

牛顿迭代法在很多领域(例如极值搜索、计算机控制、计算机分形图形生策划狗奴以及计算机仿真技术等领域)都有中极为广泛的应用，因此其也被广泛应用与工业生产与制作业中。

然而，目前的改进算法多是基于牛顿切线法中的倒数近似计算方法的多种改进，而基本的迭代形式和牛顿迭代法并没有明显的区别，这些方法存在这迭代速度慢等问题。

技术实现要素：

为解决上述问题，本发明提供了一种用于工控领域的信号获取方法，所述方法包括：

柔化函数确定步骤，获取工控领域中可测信号的数值，根据所述可测信号与待求解信号的关系构建待求解高次方程模型，根据所述待求解高次方程模型构建柔化函数；

迭代递推模型确定步骤，根据所述柔化函数构造迭代递推模型；

循环迭代步骤，基于所述迭代递推模型进行循环迭代，并判断当前迭代循环是否满足跳出迭代循环条件，如果满足，则将当前迭代循环中的待求解信号的数值作为所述待求解信号的最终取值。

根据本发明的一个实施例，在所述柔化函数确定步骤中，计算所述待求解高次方程模型的导数，结合可调正参数来构建所述柔化函数。

根据本发明的一个实施例，根据如下表达式构建所述柔化函数：

其中，x_n表示第n次迭代循环中待求解信号的数值，D(x_n)表示第n次迭代循环所对应的柔化函数的取值，k和ε均表示用于调整迭代速率的可调正参数，F′(x_n)表示第n次迭代循环所对应的待求解高次方程模型F(x_n)的导数。

根据本发明的一个实施例，所述可调正参数k的取值越大，所述迭代递推模型收敛得越快。

根据本发明的一个实施例，根据如下表达式构造所述迭代递推模型：

x_n+1＝x_n-D(x_n)

其中，x_n+1和x_n分别表示第n+1次和第n次迭代循环中待求解信号的数值，D(x_n)表示柔化函数。

根据本发明的一个实施例，如果迭代次数达到预设迭代次数阈值，则判定此时满足跳出迭代循环条件。

根据本发明的一个实施例，如果当前迭代循环中待求解信号的数值与前一迭代循环中待求解信号的数值的差值的绝对值小于或等于预设差值阈值，则判定此时满足跳出迭代循环条件。

根据本发明的一个实施例，所述待求解信号的初始值随机设定。

根据本发明的一个实施例，所述可测信号为铂电阻的阻值，所述待求解信号为所述铂电阻所测量的物质的温度。

根据本发明的一个实施例，所述待求解高次方程模型表示为：

F(x)＝R₀(1+Ax+Bx²)+C(x-100)x³-G

其中，F(x)表示待求解高次方程模型，R₀、A、B和C均表示已知计算系数，x表示温度值，G表示所述铂电阻的阻值。

本发明所提供的用于工控领域的信号获取方法是一种基于非线性柔化函数的迭代搜索求根方法，该方法根据待求根方程模型与其导数信息，构造了一种迭代速率可调的非线性迭代模型，最终可以通过迭代在初始值附近进行方程根的搜索，从而解决高次方程求根问题，这样便可以得到所需要的待求解信号的最终取值。

与现有技术相比，本发明提供的方法求解过程更加快速，通过还能够通过调节可调正参数的取值来调节迭代求根的速率。该方法可以解决目前采用牛顿迭代法进行计算机搜索求根所存在的搜索速度慢、迭代时间长且迭代速率不可调的缺陷。

本发明的其它特征和优点将在随后的说明书中阐述，并且，部分地从说明书中变得显而易见，或者通过实施本发明而了解。本发明的目的和其他优点可通过在说明书、权利要求书以及附图中所特别指出的结构来实现和获得。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要的附图做简单的介绍：

图1是根据本发明一个实施例的用于工控领域的信号获取方法的实现流程图；

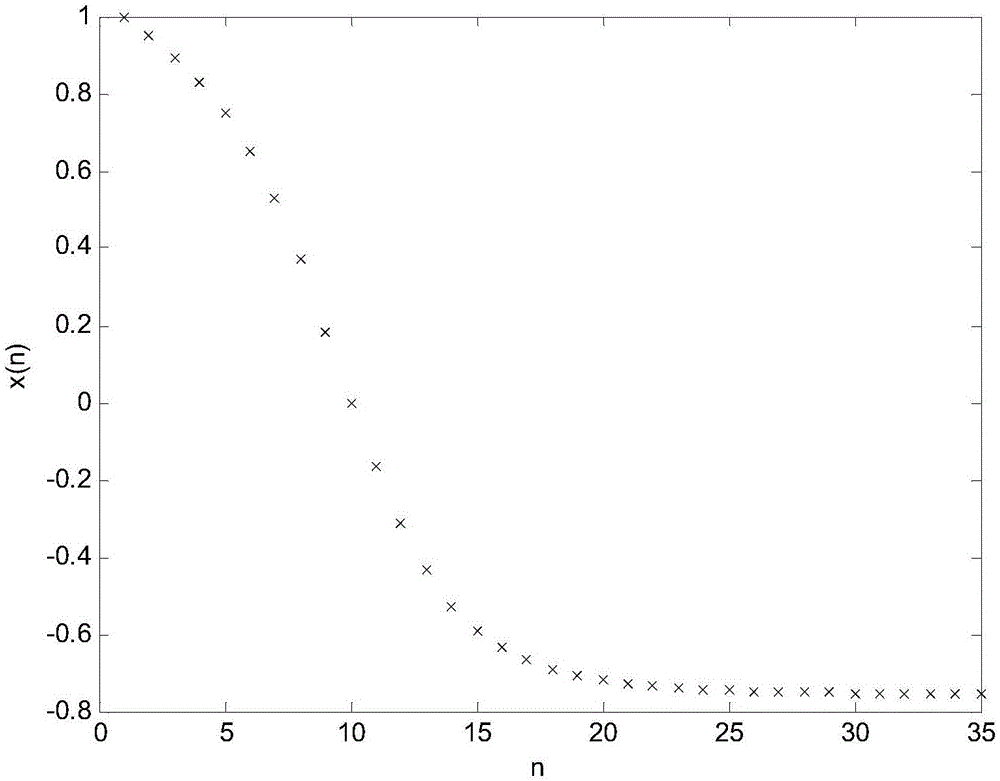
图2是根据本发明一个实施例的对方程F(x)＝x⁵+x+1＝0进行求解的仿真曲线示意图；

图3是根据本发明一个实施例的对方程F(x)＝x⁵-32＝0进行求解的仿真曲线示意图；

图4是根据本发明一个实施例的参数调整后的仿真曲线示意图。

具体实施方式

以下将结合附图及实施例来详细说明本发明的实施方式，借此对本发明如何应用技术手段来解决技术问题，并达成技术效果的实现过程能充分理解并据以实施。需要说明的是，只要不构成冲突，本发明中的各个实施例以及各实施例中的各个特征可以相互结合，所形成的技术方案均在本发明的保护范围之内。

同时，在以下说明中，出于解释的目的而阐述了许多具体细节，以提供对本发明实施例的彻底理解。然而，对本领域的技术人员来说显而易见的是，本发明可以不用这里的具体细节或者所描述的特定方式来实施。

另外，在附图的流程图示出的步骤可以在诸如一组计算机可执行指令的计算机系统中执行，并且，虽然在流程图中示出了逻辑顺序，但是在某些情况下，可以以不同于此处的顺序执行所示出或描述的步骤。

针对现有技术中所存在的上述问题，本实施例提供了一种新的用于工控领域的信号获取方法，该方法是一种基于柔化函数的非线性迭代搜索求根方法，图1示出了本实施例中该方法的实现流程图。

如图1所示，本实施例所提供的方法在步骤S101中获取工控领域中可测信号的数值，并在步骤S102中根据该可测信号与待求解信号的关系构建待求解高次方程模型。

在得到待求解高次方程模型后，该方法在步骤S103中根据该待求解高次方程模型构建柔化函数。具体地，在构建柔化函数的过程中，该方法优选地首先计算上述待求解高次方程的导数，随后根据上述待求解高次方程以及导数以及可调正参数来构建柔化函数。

具体地，本实施例中，该方法在步骤S103中优选地根据如下表达式来确定柔化函数：

其中，x表示待求解信号的数值，D(x)表示柔化函数，F′(x_n)表示待求解高次方程模型F(x_n)的导数，k和ε均表示用于调整迭代速率的可调正参数。其中，可调正参数k和ε关系着迭代递推模型的收敛速率。具体地，本实施例中，可调正参数k的取值越大，迭代递推模型收敛得越快。

对于各个迭代循环来说，其对应的柔化函数的取值可以根据如下表达式计算得到：

其中，x_n表示第n次迭代循环中待求解信号的数值，D(x_n)表示第n次迭代循环所对应的柔化函数的取值，k和ε均表示用于调整迭代速率的可调正参数，F′(x_n)表示第n次迭代循环所对应的待求解高次方程模型F(x_n)的导数。

例如，将待求解方程记为F(x)，例如选取F(x)＝x⁵+x+1，那么待求解方程的导数则为F′(x)＝5x⁴+1。

在得到柔化函数后，该方法将在步骤S104中根据步骤S103中所确定出的柔化函数来构建迭代递推模型。本实施例中，当前迭代循环中自变量的取值x_n+1为前一迭代循环中自变量的取值x_n与对应的柔化函数的取值之差，即存在：

x_n+1＝x_n-D(x_n) (3)

该方法在步骤S105中便可以利用步骤S104中所得到的迭代递推模型来进行循环迭代。本实施例中，迭代初始值(即待求解信号的初始值)以及确定预设迭代次数阈值可以事先设定。其中，本实施例中，待求解信号的初始值优选地可以随机设定，例如将待求解信号的初始值x₀设置为1。需要指出的是，在本发明的不同实施例中，上述预设迭代次数阈值的具体取值可以根据实际需要设定为不同的合理值，在此并不对该预设迭代次数阈值的具体取值进行限定。

在上述循环迭代过程中，该方法会在步骤S106中持续判断当前迭代循环是否满足跳出迭代循环条件。如果满足跳出迭代循环条件，该方法会在步骤S107中将当前迭代循环中自变量的取值来作为待求解方程的根，即将当前迭代循环中的待求解信号的数值作为该待求解信号的最终取值；而如果不满足跳出迭代循环条件，那么该方法则会继续执行步骤S105。

本实施例中，在判断当前迭代循环是否满足跳出迭代循环条件时，该方法会计算当前迭代循环中自变量(即待求解信号)的取值x_n+1与前一迭代循环中自变量的取值x_n的差值的绝对值Δ_n+1，即存在：

Δ_n+1＝|x_n+1-x_n| (4)

在得到绝对值Δ_n+1后，该方法会进一步判断该绝对值Δ_n+1是否小于或等于预设差值阈值ξ，即判断Δ_n+1≤ξ是否成立。如果绝对值Δ_n+1小于或等于预设差值阈值ξ，那么该方法则会判定此时满足跳出迭代循环条件；而如果绝对值Δ_n+1大于预设差值阈值ξ，那么该方法则会判定此时不满足跳出迭代循环条件，从而继续进行循环迭代。

本实施例中，在判断当前迭代循环是否满足跳出迭代循环条件时，该方法还会判断当前迭代循环是否达到预设迭代次数阈值，如果达到预设迭代次数阈值，那么则会判定次数满足迭代循环条件。

需要指出的是，在本发明的不同实施例中，上述预设迭代次数阈值可以根据实际需要配置为不同的合理值，本发明不限于此。

以如下程序为例，本实施例利用上述方法对方程F(x)＝x⁵+x+1＝0进行待求解信号的获取。

图2示出了利用本实施例所提供的方法对方程F(x)＝x⁵+x+1＝0进行求解的仿真曲线示意图。其中，可调正参数k的取值为0.5，可调正参数ε的取值为2。从图2中可以看出，对于该待求解方程来说，该方法在第35次迭代循环得到了该方程的解。

图3示出了利用本实施例所提供的方法对方程F(x)＝x⁵-32＝0进行求解的仿真曲线示意图。其中，可调正参数k的取值为0.5，可调正参数ε的取值为2。从图3中可以看出，对于该待求解方程来说，该方法大约经过90次的迭代得到了最终的正确结果2。

而如果进一步增大可调正参数k和ε的取值，例如将可调正参数k的取值调整为3，将可调正参数ε的取值调整为4，那么利用本方法可以得到如图4所示的仿真曲线示意图。对比图3和图4可以看出，通过增大可调正参数的取值，该方法在求解过程中所需要的迭代次数由90多次减少到了16次，因此通过增大可调正参数的取值能够有效提高迭代求根的速度，这也表明本实施例所提供的迭代求根方法是完全有效的。

本实施例所提供的信号获取方法还可以用于铂电阻测温领域。Pt100铂电阻通常与显示仪器、记录仪器以及电子计算机等设备配套使用，其可以直接测量各种工业生产控制过程中-200℃-850℃范围内的液体、蒸汽、气体等介质以及固体表面的温度。Pt100铂电阻具有抗震性能好、测温范围广、测量精度高、机械强度高以及耐压性能好等特点，并且其电阻率较大。

对于Pt100铂电阻来说，其电阻Rt与温度t之间的关系为正比例系数的单调函数，在实际测量中具有良好的重复性，因此其工业应用非常广泛。对于Pt100铂电阻来说，其电阻G与温度值x之间的关系可以表示为：

G＝R₀(1+Ax+Bx²)+C(x-100)x³ (5)

其中，R₀、A、B和C均表示已知计算系数。例如，已知计算系数R₀、A、B和C可以分别取值为100、3.9*10^-3、-5.8*10^-7和-4.273*10^-12。

在实际工程控制应用中，对于Pt100铂电阻来说通常是测量得到其电阻值G，再通过计算来根据电阻值G来得到阈值对应的温度值x。而计算温度值x的过程也可以视为计算表达式(5)的反函数。

对于本实施例所提供的方法来说，其获取到的可测信号的数值即为Pt100铂电阻的电阻值，而根据可测信号与待求解细腻好的关系所构建的待求解高次方程模型可以表示为：

F(x)＝R₀(1+Ax+Bx²)+C(x-100)x³-G (6)

其中，F(x)表示待求解高次方程模型，x表示温度值。

当某次试验测得Pt100铂电阻的阻值为84.3034时，那么利用本实施例所提供的方法可以将温度的求解过程转换为对上述待求解高次方程模型的求解过程，即计算使得F(x)＝0的情况下x的取值。利用本实施例所提供的方法最终可以求得温度值为-40.01，通过验证，该温度值与实际值相吻合。

需要指出的是，本实施例所提供的方法还可以应用于其他合理的工控场景下。例如，在本发明的其他实施例中，该方法不仅可以用于求解高炉物料平衡，还可以应用于软土路基沉降分析领域。高炉数学模型建立在反应动力学和传输现象理论基础之上，是详细分析炉内状态和精确预测高炉操作性能的有效工具。物料平衡建立在物质不灭的基础上，它可以用物料的平衡式来表示。

在对生产高炉建模和求解时，通常把已知的炉料、鼓风以及喷吹等数据当输入量，通过物料平衡和其它工艺计算来求出诸如铁水、炉渣、煤气等输出量。典型如在炉体模拟模型、硅预报模型、最小燃料比模型和质量与能量平衡模型等均要建立各化学元素的平衡求解铁水、炉渣数据等。如何有效地对建立的平衡等式进行求解，对问题解决的效率以及模型软件的成功建立至关重要。

在上述求解过程中，现有方法多采用牛顿迭代法来进行求解，然而这种方法存在搜索速度慢、迭代时间长以及迭代速率不可调等缺陷。而本实施例所提供的方法能够有效提高上述求解过程中搜索求根的速度，并且还能够有效缩短迭代时长。同时，通过调整可调正参数的取值，该方法还可以实现对迭代速率的调整。

从上述描述中可以看出，本实施例所提供的用于工控领域的信号获取方法是一种基于非线性柔化函数的迭代搜索求根方法，该方法根据待求根方程模型与其导数信息，构造了一种迭代速率可调的非线性迭代模型，最终可以通过迭代在初始值附近进行方程根的搜索，从而解决高次方程求根问题，这样便可以得到所需要的待求解信号的最终取值。

与现有技术相比，本实施例所提供的方法求解过程更加快速，通过还能够通过调节可调正参数的取值来调节迭代求根的速率。该方法可以解决目前采用牛顿迭代法进行计算机搜索求根所存在的搜索速度慢、迭代时间长且迭代速率不可调的缺陷。

应该理解的是，本发明所公开的实施例不限于这里所公开的特定结构或处理步骤，而应当延伸到相关领域的普通技术人员所理解的这些特征的等同替代。还应当理解的是，在此使用的术语仅用于描述特定实施例的目的，而并不意味着限制。

说明书中提到的“一个实施例”或“实施例”意指结合实施例描述的特定特征、结构或特性包括在本发明的至少一个实施例中。因此，说明书通篇各个地方出现的短语“一个实施例”或“实施例”并不一定均指同一个实施例。

虽然上述示例用于说明本发明在一个或多个应用中的原理，但对于本领域的技术人员来说，在不背离本发明的原理和思想的情况下，明显可以在形式上、用法及实施的细节上作各种修改而不用付出创造性劳动。因此，本发明由所附的权利要求书来限定。