一种金线键合工艺优化方法与流程

本发明涉及一种半导体的封装领域，特别是涉及一种金线键合工艺参数优化方法。

背景技术：

金线键合是实现半导体中多芯片组件电气互连的关键技术。在多芯片组件中，通常采用金线键合技术，实现单片微波集成电路(MMIC)、集总式电阻和电容等元器件与微带线、共面波导的互连，以及微波传输线之间或与射频接地面的互连。虽然倒装芯片和载带自动焊技术发展迅速，但金线键合具有工艺简单、价格低廉、热膨胀系数小等优点，在航空航天领域的微波多芯片组件中具有突出的应用价值。

金线键合质量的优劣直接决定半导体器件的可靠性、稳定性乃至整体电性能。键合质量受控于引线材料、键合面膜层质量、键合工艺参数等多方面因素，不同工艺参数的设置及匹配会对键合质量的形成构成显著影响。只有充分掌握工艺参数对键合质量的影响规律，才可能在实际操作中准确协调各工艺参数，使键合效果达到最佳状态。

技术实现要素：

有鉴于此，本发明的目的在于提供一种金线键合工艺优化方法。

本发明的目的是通过以下技术方案来实现的，一种金线键合工艺优化方法，包括以下步骤：S1，选取影响金线键合强度的关键因素；S2，为关键因素均选取水平参数；S3，对水平参数进行数字处理，设计正交试验组，用拉力测试结果检验试验结果；S4，将步骤S3中正交试验的结果进行数学分析；S5，建立预测模型，预测金线键合工艺参数对键合质量的影响；S6，获得工艺窗口，达到工艺参数优化效果。

进一步，键合对象的材质为纯度≥99％，直径25μm的金线，键合方式为热压楔型。

进一步，所述关键因素数量为4个；关键因素的水平参数的数量为5个。

进一步，所述正交试验的正交表为L25(5⁴)。

进一步，所述数学分析方法包括以下子步骤：

S41，方差分析：

计算每个因素各个水平对应的结果的均值：

K_iN＝(该因素N取水平i时的结果之和)/k

其中N是试验选取的因素标号，k是每个参数对应水平数目；

计算偏差平方和：

其中是所有试验结果的平均值；

计算自由度f_N：

f_N＝k-1；

得到方差V_N：

V_N＝S_N/f_N；

S42，极差分析：

R_N＝max|K_iN-K_jN|＝K_Nmax-K_Nmin，

其中N是试验选取的因素标号，k是每个参数对应水平数目。

进一步，所述预测模型采用多元非线性回归建模；金线键合工艺参数的实际模型如下：

y＝f(x₁,x₂,x₃,x₄)

其中y是拉力测试结果，x₁是键合压力，x₂是键合功率，x₃是键合时间，x₄是键合温度，f是输入量与输出量之间的非线性关系函数。

由于采用以上技术方案，本发明具有以下优点：

采用本发明的金线工艺优化方法，成本和工作量控制适中，有利于比较各参数对工艺质量的影响优先级，获得准确度高的预测模型，得到工艺参数窗口，达到工艺优化目的。

本发明有利于半导体封装，获得金线键合工艺窗口，并在此基础上，获得误差在5％以内的预测模型，从而可减少优化工艺参数的实验和人力成本。

附图说明

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作进一步的详细描述，其中：

图1是本发明的流程示意图；

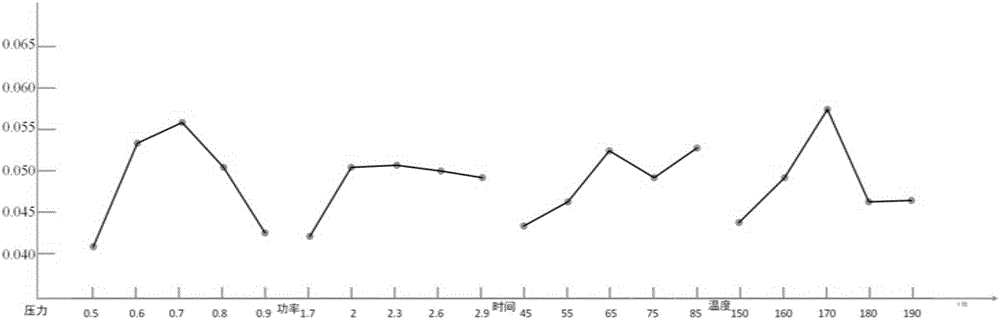
图2是本发明工艺参数正交试验的效应曲线的示意图。

具体实施方式

下面将结合附图，对本发明的优选实施例进行详细的描述。

为了实现本发明的上述目的，本发明提供了金线键合工艺优化方法，所述方法包括以下步 骤：

S1，选取影响金线键合强度的关键因素；

其中，本实施例所选取的关键因素数量为4个：键合功率，键合时间，键合压力，键合温度。

S2，为关键因素均选取水平参数：

其中，本实施例所选取的水平参数数量为5个：键合压力，超声功率，超声时间，键合温度，拉力强度。

S3，对水平参数进行数字处理，设计正交试验组，用拉力测试结果检验试验结果，如表1所示；

表1正交试验表示意图

S4，将步骤S3中正交试验的结果进行数学分析，如表2所示；

表2键合工艺参数与测试拉力值分析表

在本实施方式中，具体数据分析方法为：方差分析法和极差分析法。

方差分析法适用于分析两个或两个以上样本均值差别的显著性检验。由于多个因素的作用，所得的数据存在波动现象。造成波动的原因有两种，一种是不可控的随机因素，另一种则是研究中实验条件施加的可控因素。相较于平均值方法，方差更能反映数据的离散特征。方差分析是从观察变量的方差着手，研究众多控制变量中对结果的影响程度大小，通过分析研究不同来源的变异对于总变异的贡献大小，从而确定可控因素对研究结果的影响显著性。计算步骤如下：

计算每个因素各个水平对应的结果的均值：

K_iN＝(该因素N取水平i时的结果之和)/k，

其中N是试验选取的因素标号，k是每个参数对应水平数目。

计算偏差平方和：

其中是所有试验结果的平均值。

计算自由度：

f_N＝k-1。

计算方差：

V_N＝S_N/f_N。

极差分析法是用来表示统计资料中的变异量数，计算相对简单，可以表现出一组数据的离散程度。极差分析法可以通过对试验结果作少量的计算就能获得重要的信息，不仅可以直接比较各因素，还可以比较因素间的交互作用对试验指标的影响并从中选出最优的工艺参数。计算方法如下：

R_N＝max|K_iN-K_jN|＝K_Nmax-K_Nmin，

其中N是试验选取的因素标号，k是每个参数对应水平数目。

如表2和图2所示，从极差分析结果R值可以看出：影响旁路模块金线键合工艺拉力结果的因素排序依次为：键合压力，键合温度，超声功率，键合时间；工艺参数变化对拉力结果影响较大，表现为极差变化较大；而拉力的极差变化较小。考虑金线键合拉力测试值越大，键合质量越好，可以得出：5水平参数中相对最优的工艺参数为：键合压力0.7N，键合功率2W，键合时间85ms，键合温度170℃；从方差分析结果的V值可以看出：对拉力的工艺参数影响程度排序为：键合压力，键合温度，键合时间超声功率；这与直观分析结果有不同之处，但键合压力、温度都是排名前二的影响因素。

S5：建立拉力测试预测模型。

金线键合工艺参数之间相互耦合，之间有极其复杂的非线性关系，这都会影响金线键合质量，因此，本实施方式采用多元非线性回归建模。

本发明中，金线键合工艺参数的实际模型如下：

y＝f(x₁,x₂,x₃,x₄)

其中y是拉力测试结果，x₁是键合压力，x₂是键合功率，x₃是键合时间，x₄是键合温度，f是输入量与输出量之间的非线性关系函数。

本实施例选择工艺参数为键合压力、键合功率、键合时间和键合温度是基于键合工艺参数之间相互耦合，之间有极其复杂的非线性关系，各工艺参数对键和质量的影响难以用准确的数学模型表示。多元非线性回归建模，可以较准确揭示工艺参数与键合质量之间的内在联系。

本实施例中，四者共同作用时拉力强度与键合压力，键合功率和超声时间之间存在二次函数关系，即多元非线性回归模型为：

其中y是键合拉力强度，a,b,c,d是待求未知参数。

将正交实验结果代入，可以得到各个参数取值。首先对每组变量进行归一化处理，再采用SAS软件进行分析建模，建立多元非线性回归模型。

各个参数取值为：

a₁＝-7.564,a₂＝-6.033,a₃＝0.146,a₄＝-2.028；

b₁＝-0.158,b₂＝4.915,b₃＝-1.839,,b₄＝0.111,b₅＝-2.077,b₆＝1.608；

c₁＝-0.122,c₂＝2.857,c₃＝2.342,c₄＝1.572；

d＝14.739。

因此，回归模型为：

决定系数R²＝1-SSE/SST，

其中SSE为残差平方和，SST为总平方和。

如表3所示，模型的回归平方和远远大于残差平方和，说明自变量和因变量之间的相关性很好。

表3非线性回归模型数学分析

决定系数R²＝0.83048，说明得到的非线性回归模型可以解释83.05％的实验结果，因此该非线性回归模型拟合效果良好。

S6：获得工艺窗口，工艺优化；

验证该回归模型的误差，由于计算非线性回归模型时对数据进行了归一化处理，所以代入非线性回归模型验证误差时，要进行反归一化处理。额外选取5组非正交试验表中的数据进行检测。结果如表4所示。

表4实验实测值与非线性回归模型预测值对比

误差分析结果显示，模型的误差均小于5％，说明可以用于不同工艺参数设置时的键合拉力强度预测。

在本实施例中，工艺窗口参数为：键合压力0.7N，键合功率2W，键合时间85ms，键合温度170℃，此时拉力测试为0.71N。

最后说明的是，以上优选实施例仅用以说明本发明的技术方案而非限制，尽管通过上述优选实施例已经对本发明进行了详细的描述，但本领域技术人员应当理解，可以在形式上和细节上对其作出各种各样的改变，而不偏离本发明权利要求书所限定的范围。