基于ST‑UPFNN算法的高含硫天然气净化工艺的动态演化建模方法与流程

本发明涉及高含硫天然气净化技术领域，更为具体地，涉及一种基于ST-UPFNN算法的高含硫天然气净化工艺的动态演化建模方法。

背景技术：

高含硫天然气酸性组分含量比常规天然气高出数倍，其脱硫过程胺液循环量大、工艺流程复杂、能耗高。统计表明，脱硫单元能耗占高含硫天然气净化厂总能耗50％以上，其单位综合能耗高达1729.3MJ·t-1，属于高耗能单元。对大型净化厂而言，通过脱硫单元优化可降低能耗5％～10％。此外，高含硫天然气酸性组分浓度高，经过净化后的产品气量相对原料气流量有显著下降。为此，对高含硫天然气脱硫过程进行工艺优化，实现节能降耗，提高产率和气体加工经济效益是十分必要的。

技术实现要素：

鉴于上述问题，本发明的目的是提供一种基于ST-UPFNN算法的高含硫天然气净化工艺的动态演化建模方法，以解决上述背景技术所提出的问题。

本发明提供的基于ST-UPFNN算法的高含硫天然气净化工艺的动态演化建模方法，包括：

步骤S1：选择影响脱硫效率的工艺参数和脱硫单元的性能指标；其中，所述工艺参数包括进入尾气吸收塔的贫胺液流量、进入二级吸收塔的贫胺液流量、原料气处理量、尾气单元返回脱硫单元的半富胺液流量、一级吸收塔的胺液入塔温度、二级吸收塔的胺液入塔温度、闪蒸罐压力、一个重沸器的蒸汽消耗量、另一个重沸器的蒸汽消耗量和蒸汽预热器的蒸汽消耗量；所述脱硫单元的性能指标包括净化气中H₂S和CO₂的浓度以及净化气的产量；

步骤S2：采集预设时间的工艺参数和所述性能指标的数据，剔除误差样本后形成样本集[X,Y]；

步骤S3：对样本集[X,Y]进行归一化，形成归一化样本集取归一化样本集中前80％的样本作为训练样本，而剩余的20％样本作为测试样本；

步骤S4：基于训练样本构建神经网络模型和神经网络模型的初始状态变量X，以及，将训练样本中的作为神经网络模型的输入，将训练样本中的作为神经网络模型的输出；

其中，神经网络模型为：

其中，I_k为训练样本的矢量样本值，并作为神经网络模型的输入，为网络输入层到隐含层的神经元的连接权值，为网络输入层到隐含层的神经元的阈值，为隐含层到网络输出层的神经元的连接权值，为隐含层到网络输出层的神经元的阈值，其中，i＝1，2…S₀；j＝1，2…S₁；k＝1，2…S₂；S₀为网络输入层的神经元的数量，S₁为网络隐含层的神经元的数量，S₂为网络输出层的神经元的数量；

初始状态变量为：

步骤S5：利用ST-UPFNN算法估计神经网络模型的最优状态变量；

步骤S6：将最优状态变量作为神经网络模型的和对式(1)进行更新，获得训练样本更新后的神经网络模型；

步骤S7：将测试样本中的输入到更新后的神经网络模型，得到预测结果，将预测结果与测试样本中的实际输出进行比较，如果比较结果小于预设误差值，所构建的神经网络模型有效；否则重复上述步骤S1-S7，直至比较结果小于所述预设误差值为止。

本发明提供的基于ST-UPFNN算法的高含硫天然气净化工艺的动态演化建模方法，能够有效地跟踪装置的整个经济效益最优路线，有效克服过程干扰、设备性能变化、经济效益和生产目标的变化问题。

附图说明

通过参考以下结合附图的说明及权利要求书的内容，并且随着对本发明的更全面理解，本发明的其它目的及结果将更加明白及易于理解。在附图中：

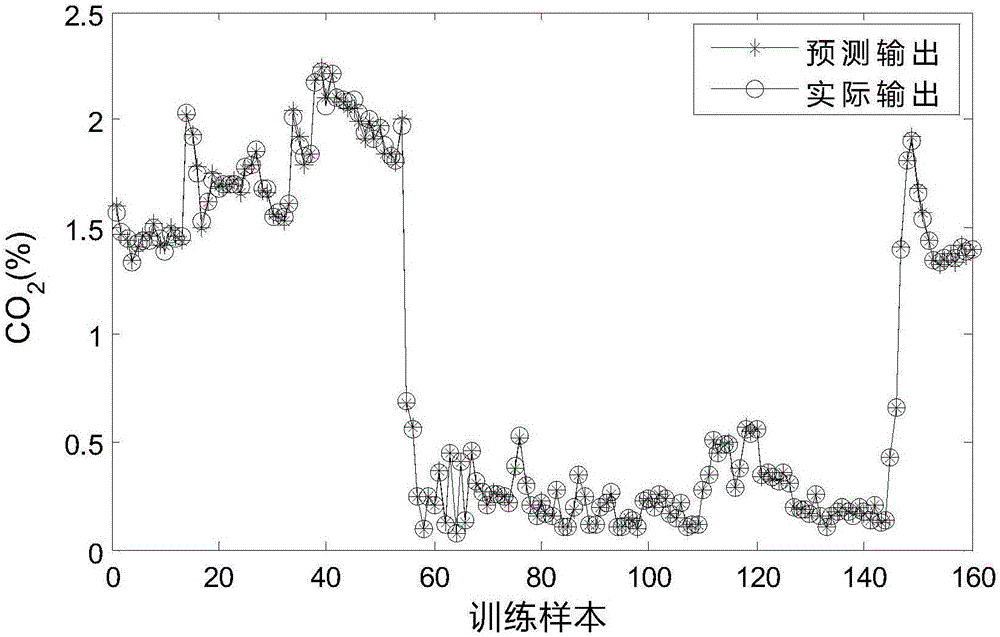
图1a-图1c为训练样本的拟合精度图；

图2a-图2c为测试样本的测试精度图；

图3为测试样本与训练样本的精度误差图。

具体实施方式

名称解释

ST-UKFNN：Strong TrackUnscentedKalman FilterNeural Network，强追踪无迹卡尔曼滤波神经网络；

ST-UPFNN：Strong TrackUnscentedParticle FilterNeuralNetwork，强追踪无迹粒子滤波神经网络，其将ST-UKFNN、粒子滤波(Particle Filter)、BP神经网络相结合。

本发明提供的基于ST-UPFNN算法的高含硫天然气净化工艺的动态演化建模方法，包括：

步骤S1：选择影响脱硫效率的工艺参数和脱硫单元的性能指标；其中，工艺参数包括进入尾气吸收塔贫的胺液流量、进入二级吸收塔的贫胺液流量、原料气处理量、尾气单元返回脱硫单元的半富胺液流量、一级吸收塔胺液入塔温度、二级吸收塔胺液入塔温度、闪蒸罐压力、一个重沸器的蒸汽消耗量、另一个重沸器的蒸汽消耗量和蒸汽预热器的蒸汽消耗量；脱硫单元的性能指标包括净化气中H₂S和CO₂的浓度以及净化气的产量。如表1所示：

表1

步骤S2：采集预设时间的工艺参数和性能指标的数据，剔除误差样本后形成样本集[X，Y]。样本集[X，Y]如下表2所示：

表2

步骤S3：对样本集[X，Y]进行归一化，形成归一化样本集取归一化样本集中前80％的样本作为训练样本，而剩余的20％样本作为测试样本。

步骤S4：基于训练样本构建神经网络模型和神经网络模型的初始状态变量X，以及，将训练样本中的作为神经网络模型的输入即将训练样本中的作为神经网络模型的输出即

其中，神经网络模型为：

其中，I_k为训练样本的矢量样本值，并作为神经网络模型的输入，为网络输入层到隐含层的神经元的连接权值，为网络输入层到隐含层的神经元的阈值，为隐含层到网络输出层的神经元的连接权值，为隐含层到网络输出层的神经元的阈值，其中，i＝1，2…S₀；j＝1，2…S₁；k＝1，2…S₂；S₀为网络输入层的神经元的数量，S₁为网络隐含层的神经元的数量，S₂为网络输出层的神经元的数量；

初始状态变量为：

步骤S5：利用ST-UPFNN算法估计神经网络模型的最优状态变量。

本发明利用ST-UPFNN算法估计所述神经网络模型的状态变量，以达到连接权值、阈值的不断调整，直到满足要求。将得到的最优状态变量作为上述所建立神经网络模型的连接权值、阈值。需要说明的是，该连接权值、阈值为通过ST-UPFNN算法调整后的连接权值、阈值，也是上述所建立的神经网络模型的全部连接权值与阈值，包括和

利用ST-UPFNN算法估计神经网络模型的最优状态变量的过程包括：

步骤S51：针对粒子滤波器设置粒子的数目N，并对抽样，得到初始粒子集并将所述初始粒子集中的每个粒子的权值均设为1/N。

其中，表示以x₀为均值、P₀为方差的正态分布采。

步骤S52：在获取(k+1)时刻的观测变量值后，利用ST-UKFNN算法对每个粒子进行(k+1)时刻的状态估计，得到最优状态估计值和协方差

利用ST-UKFNN算法对每个粒子进行状态估计的过程，包括：

步骤S521：对所述初始状态变量X进行Sigma采样，获得2n+1个采样点，初始化控制2n+1个采样点的分布状态参数α、待选参数κ，以及非负权系数β，对所述初始状态变量X的Sigma采样如下：

步骤S522：计算每个采样点的权重，每个采样点的权重如下：

其中，W_c为计算状态变量的协方差的权重，W_m为计算状态估计和观测预测时的权重，是的第一列，是的第一列。

步骤S523：通过离散时间非线性系统的状态方程将每个采样点的k时刻的最优状态变量的状态估计变换为(k+1)时刻的状态变量的状态估计以及，通过合并(k+1)时刻的状态估计的向量，获得(k+1)时刻的状态变量的状态先验估计和协方差P_k+1|k；其中，

(k+1)时刻的状态变量的状态估计为：

其中，表示k时刻的最优估计，w_k为过程噪声，其协方差矩阵Q_k为cov(w_k,w_j)＝Q_kδ_kj，

(k+1)时刻的状态变量的状态先验估计为：

(k+1)时刻的状态变量的协方差P_k+1|k为：

步骤S524：通过离散时间非线性系统的观测方程将获得的(k+1)时刻的状态变量的状态估计转化为(k+1)时刻的观测预测

其中，ν_k为观测噪声，其协方差矩阵R_k为cov(v_k,v_j)＝R_kδ_kj，

步骤S525：通过并估计(k+1)时刻的观测预测的向量，获得(k+1)时刻的先验观测预测并根据先验观测预测估计(k+1)时刻观测预测的协方差

(k+1)时刻的先验观测预测为：

(k+1)时刻观测预测的预测协方差为：

其中，在此处引入强追踪算法，即渐消因子λ_k+1增强模型的追踪能力以提高模型精度；

N_k+1＝V_k+1-βR_k+1 (12)

其中，β为弱化因子，β≥1；

步骤S526：计算(k+1)时刻的状态变量的状态先验估计与(k+1)时刻的先验观测预测之间的状态协方差状态协方差为：

步骤S527：通过建立状态协方差和预测协方差的关系，更新(k+1)时刻的状态变量的状态估计和协方差，分别获得(k+1)时刻的最优状态估计值和协方差

其中，建立的状态协方差和预测协方差的关系为：

其中，K_k+1为增益矩阵，以及，

更新后的(k+1)时刻的状态变量的状态估计为：

更新后的(k+1)时刻的状态变量的协方差P_k+1为：

将更新后的(k+1)时刻的状态变量的状态估计和协方差P_k+1分别作为(k+1)时刻的最优状态估计值和协方差

步骤S53：将最优状态估计值和初始化后的协方差作为粒子的重要性密度函数进行抽样，得到新粒子由所有新粒子组成的粒子集中的每个新粒子的正态分布概率密度值如下：

(rand为正态分布随机误差)

正态分布密度函数：

其中，N为每个新粒子的正态分布，x、μ、σ分别为正态分布函数的三个变量，p为每个新粒子的条件概率；

式(2)中，x,μ,σ分别一一对应

式(3)中，x,μ,σ分别一一对应

式(4)中，x,μ,σ分别一一对应

步骤S54：对新粒子的权值进行更新，并进行归一化处理；其中，

权值更新公式为：

权值归一化公式为：

步骤S55：根据新粒子归一化处理后的权值和重采样策略对粒子集进行重采样，获取新粒子集并求取新粒子集中每个新粒子的状态估计值

设变量u，令取u₁∈(0,1)

步骤S56：以粒子的数目N作为循环次数循环步骤S51-步骤S55的计算过程，将最后一次估计得到系统状态变量作为利用ST-UPFNN算法估计神经网络模型的最优状态变量；其中，将新粒子的状态估计值作为本时刻的最优估计付给进行下一时刻的状态估计。

神经网络模型的最优状态变量的结构参数如下：

步骤S6：将最优状态变量作为神经网络模型的和对式(1)进行更新，获得权值阈值更新后的神经网络模型。

步骤S7：将测试样本中的输入到更新后的神经网络模型，得到预测结果，将预测结果与测试样本中的实际输出进行比较，如果比较结果小于预设误差值，所构建的神经网络模型有效；否则重复上述步骤S1-S7，直至比较结果小于预设误差值为止。

本发明通过几组测试得到如下的技术效果：

图1a-图1c为训练样本的拟合精度图，其中，图1a影响脱硫效率的工艺参数为净化气H₂S浓度，图1b影响脱硫效率的工艺参数为净化气CO₂浓度，图1c影响脱硫效率的工艺参数为净化气产量。

图2a-图2c为测试样本的测试精度图，其中，图2a影响脱硫效率的工艺参数为净化气H₂S浓度，图2b影响脱硫效率的工艺参数为净化气CO₂浓度，图2c影响脱硫效率的工艺参数为净化气产量。

净化气H₂S浓度、净化气CO₂浓度和净化气产量相对误差均在2％以内，误差小于10％，故所建模有效。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应所述以权利要求的保护范围为准。