一种多孔材料隔热性能的优化控制方法与流程

本发明属于多孔材料技术领域。尤其涉及一种多孔材料隔热性能的优化控制方法。

背景技术：

在航空航天、建筑、冶金和能源等各个领域中，多孔材料中含有大量的气孔，具有密度小、比表面积大和热导率低等性能，得到广泛的应用。实际应用中，多孔材料往往是要求使用尽可能少的消耗材料达到所要求的隔热效果，同时由于多孔材料的使用环境对材料的强度有一定的要求，一般对多孔材料的气孔率有一定的范围限制。这就要求在高效利用多孔材料的隔热性能的同时，尽可能综合考虑材料的强度和使用温度等，从而实现多孔材料的多目标优化。根据实际应用对多孔材料进行设计，能更加符合应用环境，使得多孔材料的隔热性能得到更有效的利用。

国内外对多孔材料气孔分布的研究主要集中于多孔材料梯度孔的制备，如“一种梯度多孔莫来石陶瓷的制备方法”(201510875948.6)和“一种梯度多孔荃青石陶瓷的制备方法”(201510875347.5)专利技术，都是通过叠层装填，不同种混合料按其所含生物质粉的碳硅比依次增加或生物质材料自身孔结构的依次增大来装填，从而得到孔径梯度分布的梯度多孔材料，但对于如何控制梯度孔缺乏通用的技术指导。

对于多孔材料气孔的分布方面的研究(Hao J H，Chen Q，Hu K.Porosity distribution optimization of insulation materials by the variational method[J].International Journal of Heat&Mass Transfer，2016，92:1-7.)以火积耗散极值原理作为理论依据，用变分的方法研究了氧化铝质多孔纤维材料隔热性能最优时的材料密度比分布，研究基于纤维多孔材料提出，对无序排列的多孔材料不具有适用性，且缺乏相关实验和物理模型的验证。谷沁洋(谷沁洋.非均质多孔泡沫材料导热性能的研究[D].重庆大学，2013.)利用计算机程序自动建模，建立了气孔分布几何模型，在仅考虑固相导热的情况下，研究了气孔分布的非均匀性对多孔材料隔热性能的影响，由于研究过程忽略了气相导热和辐射的影响，研究规律不适用于高温条件，且未提出气孔率的控制方法。

技术实现要素：

本发明旨在克服现有技术缺陷，目的在于提供一种适应性强、符合实际和结果可靠的多孔材料隔热性能的优化控制方法，优化后的多孔材料隔热性能改善显著。

为实现上述目的，本发明采用的技术方案包括如下步骤：

步骤1、建立一维气孔率分布与热流的数学模型

设温度沿多孔材料的传热方向呈线性分布，多孔材料的导热系数K为传热方向的函数，多孔材料的一维气孔率分布与热流q的数学模型f为

式(1)中：

n表示多孔材料在传热方向设定的离散点的总数；

i表示多孔材料在传热方向设定的离散点的序号；

x_i表示多孔材料在传热方向的第i个离散点的关于气孔率P_i的数值解，-1≤x_i≤1；

R表示多孔材料气孔率P_i的连续性控制系数，R≥0，R值越小对应的相邻离散点气孔率P_i连续性越低，反之亦然；

L表示多孔材料在传热方向的长度，m；

△x表示多孔材料在传热方向设定的相邻离散点间的距离，

q表示多孔材料在传热方向的热流，W/m²；

式(2)中：

T₁表示多孔材料的高温端温度，K；

T₂表示多孔材料的低温端温度，K；

T_i表示多孔材料在传热方向的第i个离散点的温度，K；

e表示多孔材料固相气孔壁的辐射率；

r表示多孔材料的气孔半径，m；

δ为波尔兹曼常数，δ＝5.67×10^-8W/(m²·K⁴)；

Ka_i表示第i个离散点的多孔材料的空气导热系数，W·m^-1·K^-1；

Ka_i＝2.3×10^-9×T_i²+4.9×10^-5×T_i+0.03

Kc_i表示第i个离散点的多孔材料的固相导热系数，W·m^-1·K^-1；

P_min表示多孔材料气孔率的最小值；

P_max表示多孔材料气孔率的最大值；

P_i表示多孔材料在传热方向第i个离散点的气孔率；

步骤2、建立目标函数和约束条件

目标函数：取式(1)的数学模型f的最小值。

约束条件：

式(4)中：x_i表示多孔材料在传热方向上第i个离散点的数值解，-1≤x_i≤1；

σ为常数，

步骤3、设定变量

设定下述三种变量中的一种为变量：

1)、设定连续性控制系数R为变量

当多孔材料的第i个离散点的气孔率P_i变化范围、总气孔率P、气孔半径r、固相导热系数K_c为定值时，调节式(1)中气孔率的连续性控制系数R。

2)、设定最高气孔率P_max和最低气孔率P_min为变量

当材料的气孔率连续性控制系数R、总气孔率P、气孔半径r、固相导热系数K_c为定值时，调节式(1)中最高气孔率P_max和最低气孔率P_min。

3)、设定固相导热系数K_c为变量

当材料的最高气孔率P_max和最低气孔率P_min、气孔率连续性控制系数R、气孔率P、气孔半径r为定值时，调节式(1)中固相导热系数K_c。

步骤4、用MATLAB软件进行优化

利用MATLAB软件，对步骤2所述的目标函数和约束条件分别编写MATLAB文件，将所编写的MATLAB文件分别添加到MATLAB的优化路径中，然后对步骤3所设定的变量，分别建立调用优化工具箱中f_mincon函数的命令文件，将所述命令文件复制到MATLAB命令窗口中运行求解，得到式(1)的数学模型f的最小值和各离散点的x_i值。

步骤5、用式(3)将步骤4得到的各离散点的数值解x_i转化为各离散点的气孔率P_i

所述第i个离散点的多孔材料的固相导热系数Kc_i或从文献中获知，或对固相导热系数Kc_i未知的多孔材料进行致密压片处理，测试致密压片后的多孔材料在各温度下的导热系数，然后将测试得到的导热系数拟合成温度的函数，得到第i个离散点的多孔材料的固相导热系数Kc_i。

由于采用上述技术方案，本发明与现有技术相比具有如下积极效果；

1本发明对多孔材料气孔分布的指导不仅仅局限于某一种多孔材料，具有普遍的应用意义，适用性强。

2本发明综合考虑了导热和辐射传热对多孔材料隔热性能的影响，导热传热的模型采用并联模型λ_c＝(1-P)×Kc+P×Ka，辐射传热的模型采用λ_r＝8/3PerδT³，更加符合多孔材料的实际传热情况。

3本发明用实验和数值建模的方法分别进行了验证，结果可靠，隔热性能显著改善。

用添加造孔剂法分别制备了总气孔率P为0.5的均匀分布和优化分布的氧化铝质多孔材料，用平板导热法测试了两种试样的导热系数，在1173K时，总气孔率P为0.5的均匀分布的氧化铝质多孔材料的导热系数为0.87，而总气孔率P为0.5的优化分布的氧化铝质多孔材料的导热系数为0.74，隔热性能的改善率达到14.9％；而本发明结果的改善率为16.1％，误差为7.5％，在合理范围内，总体趋势一致。

用数值模拟的方法分别建立了总P气孔率为0.5的均匀分布和优化分布的氧化铝质多孔材料模型，并计算了材料的有效导热系数，计算结果表明在两端温度分别为1273K和1073K时，总气孔率P为0.5的均匀分布的氧化铝质多孔材料模型计算得到的导热系数为0.84，而总气孔率P为0.5的优化分布的氧化铝质多孔材料模型计算得到的导热系数为0.70，隔热性能的改善率达到16.7％，而本发明结果的改善率为16.1％，误差为4.3％，在合理范围内，总体趋势一致。

因此，本发明具有适应性强、符合实际和结果可靠的特点，优化后的多孔材料隔热性能显著改善。

附图说明

图1为本发明的一种流程图；

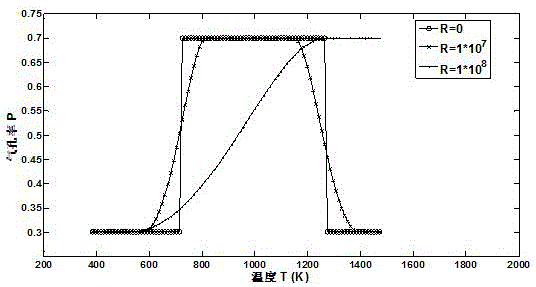
图2为莫来石Al₆Si₂O₁₃质多孔材料取不同连续性控制系数R值时的气孔率优化分布图；

图3为多孔材料取不同固相导热系数Kc_i时的气孔率优化分布图；

图4为氧化铝质多孔材料取不同气孔率波动范围(P_min，P_max)时的气孔率优化分布图。

具体实施方法

下面结合附图和具体实施方式对本发明作进一步描述，并非对本发明的保护范围的限制。

实施例1

一种莫来石Al₆Si₂O₁₃质多孔材料隔热性能的优化控制方法。本实施例所述优化控制方法如图1所示：

步骤1、建立一维气孔率分布与热流的数学模型

设温度沿莫来石Al₆Si₂O₁₃质多孔材料传热方向呈线性分布，莫来石Al₆Si₂O₁₃质多孔材料的导热系数K为传热方向的函数，莫来石Al₆Si₂O₁₃质多孔材料的一维气孔率分布与热流q的数学模型f为

式(1)中：

n表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向设定的离散点的总数，n＝100；

i表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向设定的离散点的序号；

x_i表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向的第i个离散点的关于气孔率P_i的数值解，-1≤x_i≤1；

R表示莫来石Al₆Si₂O₁₃质多孔材料气孔率P_i的连续性控制系数，R值越小对应的相邻离散点气孔率P_i连续性越低，反之亦然；

L表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向的长度，L＝0.2m；

△x表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向设定的相邻离散点间的距离，△x＝2×10^-3m；

q表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向的热流，W/m²；

式(2)中：

T₁表示莫来石Al₆Si₂O₁₃质多孔材料的高温端温度，T₁＝1473K；

T₂表示莫来石Al₆Si₂O₁₃质多孔材料的低温端温度，T₂＝373K；

T_i表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向的第i个离散点的温度，

e表示莫来石Al₆Si₂O₁₃质多孔材料固相气孔壁的辐射率，e＝0.8；

r表示莫来石Al₆Si₂O₁₃质多孔材料的气孔半径，r＝1×10^-6m；

δ为波尔兹曼常数，δ＝5.67×10^-8W/(m²·K⁴)；

Ka_i表示第i个离散点的莫来石Al₆Si₂O₁₃质多孔材料的空气导热系数，Ka_i＝2.3×10^-9×T_i²+4.9×10^-5×T_i+0.03，W·m^-1·K^-1；

Kc_i表示第i个离散点的莫来石Al₆Si₂O₁₃质多孔材料的固相导热系数；

P_min表示莫来石Al₆Si₂O₁₃质多孔材料气孔率的最小值，P_min＝0.3；

P_max表示莫来石Al₆Si₂O₁₃质多孔材料气孔率的最大值，P_max＝0.7；

P_i表示莫来石Al₆Si₂O₁₃质多孔材料在传热方向第i个离散点的气孔率，

本实施例所述第i个离散点的莫来石Al₆Si₂O₁₃质多孔材料的固相导热系数Kc_i是：将莫来石Al₆Si₂O₁₃质多孔材料进行致密压片处理，测试致密压片后的莫来石Al₆Si₂O₁₃质多孔材料在各温度下的导热系数，然后将测试得到的导热系数拟合成温度的函数，得到第i个离散点的莫来石Al₆Si₂O₁₃质多孔材料的固相导热系数Kc_i

Kc_i＝-2.28×10^-9T_i³+9.11×10^-6T_i²-1.2×10^-2T_i+9.01,W·m^-1·K^-1。

步骤2、建立目标函数和约束条件

目标函数：取式(1)的数学模型f的最小值。

约束条件：取总气孔率P＝0.5，所以

步骤3、设定变量

本实施例设定连续性控制系数R为变量。当莫来石Al₆Si₂O₁₃质多孔材料的第i个离散点的气孔率P_i变化范围、总气孔率P、气孔半径r和各离散点的莫来石Al₆Si₂O₁₃质多孔材料的固相导热系数Kc_i取本实施例式(1)中对应的数值时，调节式(1)中气孔率的连续性控制系数R，分别取R＝0、R＝1×10⁷和R＝1×10⁸。

步骤4、利用MATLAB软件进行优化

利用MATLAB软件，对步骤2所述的目标函数和约束条件分别编写MATLAB文件，将所编写的MATLAB文件分别添加到MATLAB的优化路径中；然后对步骤3所设定的3个不同的连续性控制系数R，分别建立调用优化工具箱中f_mincon函数的命令文件，将所述命令文件复制到MATLAB命令窗口中运行求解：

当R＝0时，得到式(1)的数学模型f的最小值f_min和各离散点的x_i值：

f_min＝10144.3。

x₁＝-1；x₂＝-1；x₃＝-1；…；x₉₈＝-1；x₉₉＝-1；x₁₀₀＝-1。

当R＝1×10⁷时，得到式(1)的数学模型f的最小值f_min和各离散点的x_i值：

f_min＝10837.2。

x₁＝-1；x₂＝-1；x₃＝-1；…；x₉₈＝-1；x₉₉＝-1；x₁₀₀＝-1。

当R＝1×10⁸时，得到式(1)的数学模型f的最小值f_min和各离散点的x_i值：

f_min＝11400.5。

x₁＝1；x₂＝1；x₃＝1；…；x₉₈＝-1；x₉₉＝-1；x₁₀₀＝-1。

步骤5、用式(3)将步骤4得到的各离散点的数值解x_i转化为各离散点对应的气孔率P_i。

当R＝0时：

P₁＝0.3；P₂＝0.3；P₃＝0.3；…；P₉₈＝0.3；P₉₉＝0.3；P₁₀₀＝0.3。

当R＝1×10⁷时：

P₁＝0.3；P₂＝0.3；P₃＝0.3；…；P₉₈＝0.3；P₉₉＝0.3；P₁₀₀＝0.3。

当R＝1×10⁸时：

P₁＝0.7；P₂＝0.7；P₃＝0.7；…；P₉₈＝0.3；P₉₉＝0.3；P₁₀₀＝0.3。

根据各离散点莫来石Al₆Si₂O₁₃质多孔材料的温度T_i和各离散点气孔率P_i，得到如图2所示的莫来石Al₆Si₂O₁₃质多孔材料取不同连续性控制系数R值时的气孔率优化分布图。由图2可知，优化隔热性能后的莫来石Al₆Si₂O₁₃质多孔材料的气孔分布趋于：高温端高气孔率分布，低温端低气孔率分布；随着连续性控制系数R值的增大，隔热性能的改善率降低。

实施例2

一种不同固相基质多孔材料隔热性能的优化控制方法。本实施例所述优化控制方法如图1所示：

步骤1、建立一维气孔率分布与热流的数学模型

设温度沿不同固相基质多孔材料传热方向呈线性分布，不同固相基质多孔材料的导热系数K为传热方向的函数，不同固相基质多孔材料的一维气孔率分布与热流q的数学模型f为

式(1)中：

n表示不同固相基质多孔材料在传热方向设定的离散点的总数，n＝50；

i表示不同固相基质多孔材料在传热方向设定的离散点的序号；

x_i表示不同固相基质多孔材料在传热方向的第i个离散点的关于气孔率P_i的数值解,-1≤x_i≤1；

R表示不同固相基质多孔材料气孔率P_i的连续性控制系数，R值越小对应的相邻离散点气孔率P_i连续性越低，反之亦然，R＝1×10⁷；

L表示不同固相基质多孔材料在传热方向的长度，L＝0.4m；

△x表示不同固相基质多孔材料在传热方向设定的相邻离散点间的距离，△x＝8×10^-3m；

q表示不同固相基质多孔材料在传热方向的热流，W/m²；

式(2)中：

T₁表示不同固相基质多孔材料的高温端温度，T₁＝1673K；

T₂表示不同固相基质多孔材料的低温端温度，T₂＝973K；

T_i表示不同固相基质多孔材料在传热方向的第i个离散点的温度，

e表示不同固相基质多孔材料固相气孔壁的辐射率，e＝0.9；

r表示不同固相基质多孔材料的气孔半径，r＝1×10^-5m；

δ为波尔兹曼常数，δ＝5.67×10^-8W/(m²·K⁴)；

Ka_i表示第i个离散点的不同固相基质多孔材料的空气导热系数，从文献知：Ka_i＝2.3×10^-9×T_i²+4.9×10^-5×T_i+0.03，W·m^-1·K^-1；

Kc_i表示第i个离散点的不同固相基质多孔材料的固相导热系数，W·m^-1·K^-1；

P_min表示不同固相基质多孔材料气孔率的最小值，P_min＝0.25；

P_max表示不同固相基质多孔材料气孔率的最大值，P_max＝0.65；

P_i表示不同固相基质多孔材料在传热方向第i个离散点的气孔率；

步骤2、建立目标函数和约束条件

目标函数：取式(1)的数学模型f的最小值；

约束条件：取总气孔率P＝0.4，所以

步骤3、设定变量

本实施例设定各离散点的不同固相基质多孔材料的固相导热系数Kc_i为变量。当不同固相基质多孔材料的最高气孔率P_max和最低气孔率P_min、气孔率连续性控制系数R、总气孔率P和气孔半径r取本实施例式(1)中对应的数值时，调节式(1)中各离散点的不同固相基质多孔材料的固相导热系数Kc_i，分别取各离散点的橄榄石质多孔材料的固相导热系数Kc_i＝-3.139×10^-9T_i³+1.187×10^-5T_i²-1.563×10^-2T_i+9.635、各离散点的橄榄石质多孔材料的固相导热系数Kc_i＝-5.8×10^-9T_i³+2.4×10^-5T_i²-0.035T_i+21和各离散点的氧化锆质多孔材料的固相导热系数Kc_i＝4.59×10^-8T_i²+3.06×10^-4T_i+1.82。

步骤4、用MATLAB软件进行优化

利用MATLAB软件，对步骤2所述的目标函数和约束条件分别编写MATLAB文件，将所编写的MATLAB文件分别添加到MATLAB的优化路径中，然后对步骤3所设定的各离散点的3个不同固相基质多孔材料的固相导热系数Kc_i，分别建立调用优化工具箱中f_mincon函数的命令文件，将所述命令文件复制到MATLAB命令窗口中运行求解：

当各离散点的橄榄石质多孔材料的固相导热系数

Kc_i＝-3.139×10^-9T_i³+1.187×10^-5T_i²-1.563×10^-2T_i+9.635时，式(1)的数学模型f的最小值f_min和各离散点的x_i值为：

f_min＝2313.07。

x₁＝1；x₂＝1；x₃＝1；…；x₄₈＝-1；x₄₉＝-1；x₅₀＝-1。

当各离散点的氧化铝质多孔材料的固相导热系数

Kc_i＝-5.8×10^-9T_i³+2.4×10^-5T_i²-0.035T_i+21时，式(1)的数学模型f的最小值f_min和各离散点的x_i值为：

f_min＝3009.7。

x₁＝1；x₂＝1；x₃＝1；…；x₄₈＝-1；x₄₉＝-1；x₅₀＝-1。

当各离散点的氧化锆质多孔材料的固相导热系数Kc_i＝4.59×10^-8T_i²+3.06×10^-4T_i+1.82时，得到式(1)的数学模型f的最小值f_min和各离散点的x_i值：

f_min＝2230.63。

x₁＝-1；x₂＝-1；x₃＝-1；…；x₄₈＝1；x₄₉＝1；x₅₀＝1。

步骤5、用式(3)将步骤4得到的各离散点的数值解x_i转化为各离散点对应的气孔率P_i

当各离散点的橄榄石质多孔材料的固相导热系数

Kc_i＝-3.139×10^-9T_i³+1.187×10^-5T_i²-1.563×10^-2T_i+9.635时：

P₁＝0.65；P₂＝0.65；P₃＝0.65；…；P₄₈＝0.25；P₄₉＝0.25；P₅₀＝0.25。

当各离散点的氧化铝质多孔材料的固相导热系数

Kc_i＝-5.8×10^-9T_i³+2.4×10^-5T_i²-0.035T_i+21时：

P₁＝0.65；P₂＝0.65；P₃＝0.65；…；P₄₈＝0.25；P₄₉＝0.25；P₅₀＝0.25。

当各离散点的氧化锆质多孔材料的固相导热系数Kc_i＝4.59×10^-8T_i²+3.06×10^-4T_i+1.82时：

P₁＝0.25；P₂＝0.25；P₃＝0.25；…；P₄₈＝0.65；P₄₉＝0.65；P₅₀＝0.65。

根据各离散点不同固相基质多孔材料的温度T_i和各离散点气孔率P_i，可得到如图3所示各离散点的不同固相基质多孔材料取不同固相导热系数Kc_i时的气孔率优化分布图。由图3可知，优化隔热性能后的氧化铝质和橄榄石质多孔材料的气孔分布趋于：高温端高气孔率分布，低温端低气孔率分布；优化隔热性能后的氧化锆质多孔材料气孔的气孔分布趋于：高温端低气孔率分布，低温端高气孔率分布。

实施例3

一种氧化铝质多孔材料隔热性能的优化控制方法。本实施例所述优化控制方法如图1所示：

步骤1、建立一维气孔率分布与热流的数学模型

设温度沿氧化铝质多孔材料传热方向呈线性分布，氧化铝质多孔材料的导热系数K为传热方向的函数，氧化铝质多孔材料的一维气孔率分布与热流q的数学模型f为

式(1)中：

n表示氧化铝质多孔材料在传热方向设定的离散点的总数，n＝60；

i表示氧化铝质多孔材料在传热方向设定的离散点的序号；

x_i表示氧化铝质多孔材料在传热方向的第i个离散点的关于气孔率P_i的数值解，

-1≤x_i≤1；

R表示氧化铝质多孔材料气孔率P_i的连续性控制系数，R值越小对应的相邻离散点气孔率P_i连续性越低，反之亦然，R＝1×10⁶；

L表示氧化铝质多孔材料在传热方向的长度，L＝0.3m；

△x表示氧化铝质多孔材料在传热方向设定的相邻离散点间的距离，△x＝5×10^-3m；

q表示氧化铝质多孔材料在传热方向的热流，W/m²；

式(2)中：

T₁表示氧化铝质多孔材料的高温端温度，T₁＝1573K；

T₂表示氧化铝质多孔材料的低温端温度，T₂＝873K；

T_i表示氧化铝质多孔材料在传热方向的第i个离散点的温度，

e表示氧化铝质多孔材料固相气孔壁的辐射率，e＝0.9；

r表示氧化铝质多孔材料的气孔半径，r＝1×10^-6m；

δ为波尔兹曼常数，δ＝5.67×10^-8W/(m²·K⁴)；

Ka_i表示第i个离散点的氧化铝质多孔材料的空气导热系数，

Ka_i＝2.3×10^-9×T_i²+4.9×10^-5×T_i+0.03，W·m^-1·K^-1；

Kc_i表示第i个离散点的氧化铝质多孔材料的固相导热系数，从文献知：

Kc_i＝-5.8×10^-9T_i³+2.4×10^-5T_i²-0.035T_i+21,W·m^-1·K^-1；

P_min表示氧化铝质多孔材料气孔率的最小值；

P_max表示氧化铝质多孔材料气孔率的最大值；

P_i表示氧化铝质多孔材料在传热方向第i个离散点的气孔率，

步骤2、建立目标函数和约束条件

目标函数：取式(1)的数学模型f的最小值；

约束条件：取总气孔率P＝0.5，所以

步骤3、设定变量

本实施例设定氧化铝质多孔材料的最高气孔率P_max和最低气孔率P_min为变量。当氧化铝质多孔材料的气孔率连续性控制系数R、总气孔率P、气孔半径r和第i个离散点的氧化铝质多孔材料的固相导热系数Kc_i取本实施例式(1)中对应的数值时，调节式(1)中最高气孔率P_max和最低气孔率P_min，分别取P_max＝0.55、P_min＝0.45，P_max＝0.60、P_min＝0.40，P_max＝0.65、P_min＝0.35。

步骤4、用MATLAB软件进行优化

利用MATLAB软件，对步骤2所述的目标函数和约束条件分别编写MATLAB文件，将所编写的MATLAB文件分别添加到MATLAB的优化路径中，然后对步骤3所设定的氧化铝质多孔材料的3个不同最高气孔率P_max和最低气孔率P_min，分别建立调用优化工具箱中f_mincon函数的命令文件，将所述命令文件复制到MATLAB命令窗口中运行求解：

当氧化铝质多孔材料的最高气孔率P_max＝0.55和最低气孔率P_min＝0.45时，式(1)的数学模型f的最小值f_min和各离散点的x_i值为：

f_min＝12681.0。

x₁＝1；x₂＝1；x₃＝1；…；x₅₈＝-1；x₅₉＝-1；x₆₀＝-1。

当氧化铝质多孔材料的最高气孔率P_max＝0.60和最低气孔率P_min＝0.40时，式(1)的数学模型f的最小值f_min和各离散点的x_i值为：

f_min＝12011.1。

x₁＝1；x₂＝1；x₃＝1；…；x₅₈＝-1；x₅₉＝-1；x₆₀＝-1。

当氧化铝质多孔材料的最高气孔率P_max＝0.65和最低气孔率P_min＝0.35时，式(1)的数学模型f的最小值f_min和各离散点的x_i值为：

f_min＝11154.5。

x₁＝1；x₂＝1；x₃＝1；…；x₅₈＝-1；x₅₉＝-1；x₆₀＝-1。

步骤5、用式(3)将步骤4得到的各离散点的数值解x_i转化为各离散点对应的气孔率P_i

当氧化铝质多孔材料的最高气孔率P_max＝0.55和最低气孔率P_min＝0.45时：

P₁＝0.55；P₂＝0.55；P₃＝0.55；…；P₅₈＝0.45；P₅₉＝0.45；P₆₀＝0.45。

当氧化铝质多孔材料的最高气孔率P_max＝0.60和最低气孔率P_min＝0.40时：

P₁＝0.60；P₂＝0.60；P₃＝0.60；…；P₅₈＝0.40；P₅₉＝0.40；P₆₀＝0.40。

当氧化铝质多孔材料的最高气孔率P_max＝0.65和最低气孔率P_min＝0.35时：

P₁＝0.65；P₂＝0.65；P₃＝0.65；…；P₅₈＝0.35；P₅₉＝0.35；P₆₀＝0.35。

根据各离散点的氧化铝质多孔材料的温度T_i和各离散点气孔率P_i，得到如图4所示的氧化铝质多孔材料取不同气孔率波动范围(P_min，P_max)时的气孔率优化分布图。由图4可知，优化隔热性能后的氧化铝质多孔材料的气孔分布趋于：高温端高气孔率分布，低温端低气孔率分布；随着气孔率波动范围(P_min，P_max)的增大，隔热性能的改善率增加。

本具体实施方式与现有技术相比具有如下积极效果；

1本具体实施方式对多孔材料气孔分布的指导不仅仅局限于某一种材料，具有普遍的应用意义，适用性强。

2本具体实施方式综合考虑了导热和辐射传热对多孔材料隔热性能的影响，导热传热的模型采用并联模型λ_c＝(1-P)×Kc+P×Ka，辐射传热的模型采用λ_r＝8/3PerδT³，更加符合多孔材料的实际传热情况。

3本具体实施方式用实验和数值建模的方法分别进行了验证，具有真实可靠性。

用添加造孔剂法分别制备了总气孔率P为0.5的均匀分布和优化分布的氧化铝质多孔材料，并用平板导热法测试了两种试样的导热系数，在1173K时，总气孔率P为0.5的均匀分布的氧化铝质多孔材料的导热系数为0.87，而总气孔率P为0.5的优化分布的氧化铝质多孔材料的导热系数为0.74，隔热性能的改善率达到14.9％；而本具体实施方式结果的改善率为16.1％，误差为7.5％，在合理范围内，总体趋势一致。

用数值模拟的方法分别建立了总P气孔率为0.5的均匀分布和优化分布的氧化铝质多孔材料模型，并计算了材料的有效导热系数，计算结果表明在两端温度分别为1273K和1073K时，总气孔率P为0.5的均匀分布的氧化铝质多孔材料模型计算得到的导热系数为0.84，而总气孔率P为0.5的优化分布的氧化铝质多孔材料模型计算得到的导热系数为0.70，隔热性能的改善率达到16.7％，而本具体实施方式结果的改善率为16.1％，误差为4.3％，在合理范围内，总体趋势一致。

因此，本具体实施方式具有应用普遍，贴合实际，适用性强，真实可靠等特点。