基于半监督子块联合回归的单样本人脸识别方法与流程

本发明涉及单样本人脸识别方法，特别是涉及每个待识别对象仅有一幅训练图像的基于半监督子块联合回归的单样本人脸识别方法，属于人脸识别技术领域。

背景技术：

过去四十年中，人脸识别技术取得了显著进展，可控条件下的人脸识别技术已经基本成熟。然而在非可控条件下，由于受光照、表情、姿态、噪声、遮挡等因素的影响，人脸识别仍然是一个很有挑战性的研究问题。解决这些问题的最直接方法就是加大训练样本，但在实际应用中如身份证识别、护照识别、司法确认、准入控制等诸多实际应用中，通常只有一个训练样本可被获取，这种情况下的人脸识别问题被称之为单样本人脸识别问题(Single Sample per Person，SSPP)，其进一步加剧了非可控条件下人脸识别的难度。

从技术上讲，单样本人脸识别更加凸显了训练样本少与图像数据维数高之间的矛盾，使得许多现有的人脸识别技术要么出现严重的性能下降，要么根本无法工作，因而被公认为是最具挑战性的研究课题之一。但从实用角度讲，每人单张图像本身却具有采集容易、存储代价小、便于大范围推广等许多突出优点。因此，单样本人脸识别问题不仅具有很强的学术研究价值，而且也是人脸识别系统走向实用化过程中无可回避、必须解决的问题，解决这一问题具有重大的现实意义。

为了克服单样本识别时类内变化无法估计的问题，通用学习法(generic learning)额外引入了一个含有每人多张人脸的通用训练集(generic set)。由于人脸具有相似的类内变化，因此有可能将generic set上学习到的人脸图像变化规律用于分析单训练样本集(gallery set)中人脸图像的变化。基于上述假设，Wang等人首先提出了一个通用学习的框架(J.Wang,K.N.Plataniotis,J.Lu,A.N.Venetsanopoulos,“On solving the face recognition problem with one training sample per subject”.Pattern Recognition,2006,39(9):1746-1762)，接着Su(S.Yu,S.Shan,X.Chen,W.Gao,“Adaptive Generic Learning for Face Recognition from a Single Sample per Person”IEEE Computer Vision and Pattern Recognition.San Francisco,CA,June 2010:2699-2706)提出的自适应通用学习(Adaptive Generic Learning，AGL)方法试图利用一个从通用训练集上学到的预测模型进一步完善该假设。Kan等人(M.Kan,S.Shan,Y.Su,et al.“Adaptive discriminant learning for face recognition”.Pattern Recognition,2013,46(9):2497-2509)提出的自适应判别分析(Adaptive Discriminant Analysis)方法则基于上述自适应通用学习的思想，利用与测试样本邻近的通用集内的若干训练样本去估计测试样本的类内散度矩阵。最近，为解决单样本识别问题，文献(B.Wang,F.Zhou,W.Li,Z.Li,Q.Liao“Combining Specific Learning and Generic Learning for Single-Sample Face Recognition,”5th International Congress on Image and Signal Processing,Chongqing,Oct.2012:1219-1223)将具体学习(Specific Learning)和通用学习(Generic Learning)相结合，而Deng等人(W.Deng,J.Hu,X.Zhou,et al.“Equidistant prototypes embedding for single sample based face recognition with generic learning and incremental learning,”Pattern Recognition,2014,47(12):3738-3749)则基于“等距原型嵌入”原理提出了一种线性回归分析(linear regression Analysis，LRA)方法，并引入通用学习来提升该方法的泛化能力。

近年来，尽管通用学习方法能在一定程度上缓解单样本识别时类内变化无法估计的困境，但其依据的一般假设却并非在所有情况下都适用，例如当两个集合中的人属于不同的种族或具有不同的肤色或年龄时，以及当generic set中的类内变化无法全部覆盖gallery set中的类内变化时。因此如何找到一个能更好覆盖gallery set中类内变化的generic set，以及如何有效挖掘出两个集合中样本间的类内变化规律都是进一步研究需要考虑的问题。

技术实现要素：

本发明所要解决的技术问题是：提供基于半监督子块联合回归的单样本人脸识别方法，为单样本人脸识别问题提供了一种简单有效的解决方案。

本发明为解决上述技术问题采用以下技术方案：

基于半监督子块联合回归的单样本人脸识别方法，包括如下步骤：

步骤1，用大小相等的正方形窗口对所有类的训练人脸图像和测试人脸图像进行分块，正方形窗口滑过图像的每个像素点，在图像的每一个像素点处得到对应的一个正方形块，第k个类的训练人脸图像像素i处的正方形块所对应的向量表示为k＝1,…,K，K表示训练人脸图像的总个数或总类别数；

步骤2，利用所有类的训练人脸图像像素i处对应的正方形块构建块训练样本集其所对应的类别标签矩阵为利用所有测试人脸图像像素i处对应的正方形块构建块测试样本集Zⁱ，设其所对应的类别标签矩阵为N表示测试人脸图像的总个数；设定块训练样本集Xⁱ和块测试样本集Zⁱ到其类别标签矩阵Y和Yunlabeled的映射矩阵为Wi，联合所有像素i处对应的块训练样本集和块测试样本集，从而得到基于半监督的联合回归模型；

步骤3，通过非严格的增广拉格朗日乘法求解步骤2基于半监督的联合回归模型，得到所有像素i处的块训练样本集和块测试样本集对应的映射矩阵Wi；

步骤4，根据映射矩阵Wi，对每个测试人脸图像的各正方形块进行分类；

步骤5，识别每个测试人脸图像的各正方形块的类别后，通过投票的方式确定测试人脸图像所属的类别。

作为本发明的一种优选方案，所述步骤1的具体过程为：

1.1定义图像中任意一个像素i为中心、半径为r、大小为(2r+1)×(2r+1)的正方形块作为像素i对应的正方形块；

1.2采用边缘像素境像的方法处理图像的边缘像素，得到以图像的边缘像素为中心的正方形块。

作为本发明的一种优选方案，步骤2所述基于半监督的联合回归模型为：

其中，表示块测试样本集Zⁱ映射到[1,1,…,1]^T∈R^K时产生的误差，E＝[E¹；E²；…；E^M]，Eⁱ表示误差，W＝[W1；W2；…；WM]，α表示的误差项系数，i＝1,…,M，M表示各训练人脸图像或测试人脸图像分成的正方形块的总块数，λ表示||W||2,1的正则项系数，||·||2,1表示2,1范数，T表示转置。

作为本发明的一种优选方案，所述步骤3的具体过程为：

3.1将步骤2的基于半监督的联合回归模型转化为如下形式：

其中，W＝[W1；W2；…；WM]，Yα＝[Y,αYu]，i＝1,…,M，M表示各训练人脸图像或测试人脸图像分成的正方形块的总块数，λ表示||W||2,1的正则项系数，||·||2,1表示2,1范数，T表示转置；

3.2为3.1的目标函数引入一个辅助变量J，得到：

3.3将3.2的目标函数转换为增广拉格朗日函数L：

其中，J＝[J1；J2；…；JM]，G,H均表示拉格朗日乘子，G＝[G1；G2；…；GM]，H＝[H1；H2；…；HM]，Tr(·)表示矩阵的迹，||·||F表示F范数，μ为大于0的惩罚参数；

3.4Eα,J,W,G,H初始化为0，μ＝0.5，固定其他未知数，更新W，则模型的目标函数转化为如下求W的目标函数：

3.5求解3.4的目标函数获得W的更新公式如下：

其中，t表示迭代次数，I为单位阵；

3.6固定其他未知数，更新J，获得如下的拉格朗日子问题：

将该目标函数转化成的形式，其中，S＝J；其有如下的闭合解：

3.7固定其他未知数，通过如下方式更新Eα：

3.8上述3.7中目标函数分解为如下的M个子问题：

将该目标函数转化成的形式，其中，其有如下的闭合解：

3.9更新拉格朗日乘子：

3.10更新参数μ：μ＝min(ρμ,μmax)，其中ρ＝1.1，μmax＝10¹⁰；

3.11检查是否满足以下收敛条件：

||J^t+1-W^t+1||∞<ε

其中，ε＝10^-8，当不满足上述收敛条件时，重复3.4-3.11，直至满足收敛条件。

作为本发明的一种优选方案，步骤4所述分类的公式为：

其中，z表示一个测试人脸图像，zⁱ表示测试人脸图像像素i对应的正方形块的向量表示，label(zⁱ)表示zⁱ所属的类别标签，表示利用像素i处对应的映射矩阵Wi将zⁱ映射到其所对应的类别向量，并取类别向量中值最大的一项最为最终的类别标签，k＝1,2,…,K，K表示训练人脸图像的总个数或总类别数，T表示转置。

本发明采用以上技术方案与现有技术相比，具有以下技术效果：

1、本发明单样本人脸识别方法，一方面由于引入了更多的无标签样本来刻画类内变化，对表情、光照变化和遮挡等具有很好的鲁棒性，因而具有较高的识别精度；另一方面由于无标签的样本映射到[1,1,…,1]^T∈R^K，其在标签坐标空间中距离每一类的距离相等，并不会影响模型的判别能力。

2、本发明单样本人脸识别方法，无需特征提取，分类简单易行；且充分利用了有标签和无标签样本的信息。

附图说明

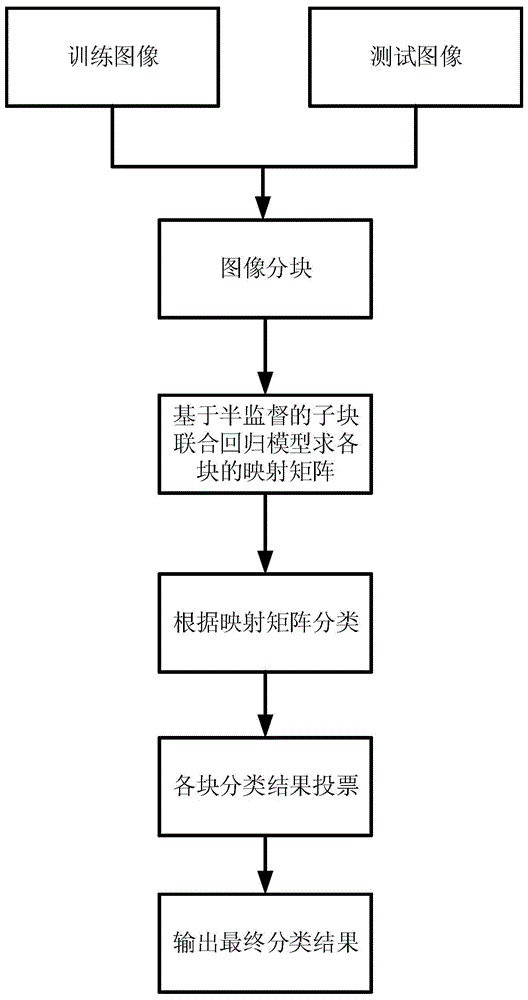
图1是本发明基于半监督子块联合回归的单样本人脸识别方法的流程图。

图2是本发明基于半监督子块联合回归的单样本人脸识别方法中图像分块示意图。

图3是本发明基于半监督子块联合回归的单样本人脸识别方法中无标签的测试样本在标签坐标空间中的几何解释示意图。

具体实施方式

下面详细描述本发明的实施方式，所述实施方式的示例在附图中示出。下面通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。

人脸变化信息实际上包含于无标签的测试人脸图像中，因此在单样本人脸识别中充分考虑无标签的测试人脸图像，可以有效学习人脸图像变化，从而避免通用学习方法对通用训练样本集的依赖以及限制。基于这一想法，本发明提出一种基于半监督子块联合回归的单样本人脸识别方法。

如图1所示，本发明基于半监督子块联合回归的单样本人脸识别方法，包括以下步骤：

1、用大小相等的正方形窗口对所有类的训练人脸图像和测试人脸图像进行分块，正方形窗口滑过图像的每个像素点，在图像的每一个像素点处得到对应的一个正方形块，具体如下：

(1)将所有单训练样本和测试样本的人脸图像划分为多个重叠的块，每个块中心对应图像的一个像素点，以该像素点为中心、半径为r的正方形窗口进行分块。也就是说图像任意一个像素i，对应一个以该像素为中心大小为(2r+1)×(2r+1)的正方形块，表示成向量形式为其中k表示第k类的样本。对所有训练人脸图像和测试人脸图像使用上述固定大小的正方形块进行分块，块中心对应图像中的像素点，如图2所示。

(2)对于图像边缘像素，采用边缘像素境像的方法来处理因大块超出图像边缘而导致其内部部分像素值缺失的现象，得到以图像边缘像素为中心的大块。

2、利用所有类的训练人脸图像像素i处对应的正方形块构建块训练样本集Xⁱ，其所对应的类别标签为Y∈R^K×K，R^K×K表示K×K的空间，假设块训练集Xⁱ到其类别标签矩阵Y的映射矩阵为Wi，通过回归模型联合求解所有子块对应的映射矩阵Wi，具体步骤如下：

(1)块训练样本集其中表示第k个或类训练人脸图像在像素i处对应的正方形块，k＝1,2,…,K，K表示训练人脸图像的总个数或总类别数；

(2)将块训练样本集对应的类别标签定义为Y∈R^K×K，假设块训练集Xⁱ到其类别标签矩阵Y的映射矩阵为Wi，该子块对应的回归模型可以表示为：Y^T＝(Xⁱ)^TWi+Eⁱ，其中Eⁱ表示误差；

(3)使用如下目标函数联合求解所有子块的映射矩阵Wi：

其中，E＝[E¹；E²；…；E^M]，W＝[W1；W2；…；WM]，i＝1,2,…,M，M表示子块个数，λ表示||W||2,1的正则项系数，||·||2,1表示2,1范数，可以有效的抑制噪声和野值。

3、取所有无标签的测试样本在像素i处的和训练样本中相同大小的子块，构成块测试样本集Zⁱ，这些测试样本的类别标签是未知的，但由于步骤2中回归模型只使用了唯一的单训练样本，无法充分学习到人脸的变化信息，因此本发明将块测试集Zⁱ映射到从而得到基于半监督的联合回归模型，该模型可以充分利用人脸的变化信息，同时所有测试样本都映射到[1,1,…,1]^T∈R^K可以保证无标签的测试样本在标签坐标空间中距离每一类的距离是相等的，这样可以在充分利用人脸变化信息的同时保证这些样本的无标签属性，其在标签坐标空间中的几何解释如图3所示。该基于半监督的子块联合回归模型如下：

其中，N表示测试样本个数，表示块测试集Zⁱ映射到[1,1,…,1]^T∈R^K时产生的误差，α表示||Eunlabeled||2,1的误差项系数。

4、通过非严格的增广拉格朗日乘法求解步骤3的半监督联合回归模型，得到所有子块对应的映射矩阵Wi，具体步骤如下：

(1)将步骤3的基于半监督的联合回归模型转化为如下形式：

其中，Yα＝[Y,αYunlabeled]，W＝[W1；W2；…；WM]，λ表示||W||2,1的正则项系数，||·||2,1表示2,1范数；

(2)为(1)的目标函数引入一个辅助变量J：

(3)将(2)的目标函数转换为增广拉格朗日函数L：

其中，Tr(·)表示矩阵的迹，J＝[J1；J2；…；JM]，G,H表示拉格朗日乘子，G＝[G1；G2；…；GM]，H＝[H1；H2；…；HM]，T表示转置，μ为大于0的惩罚参数；

(4)首先将Eα,J,W,G,H初始化为0，μ＝0.5，μmax＝10¹⁰，ρ＝1.1，ε＝10-⁸；

(5)使用交替最小化来更新Eα,J,W,G,H，固定其他未知数，更新W，则模型的目标函数可以转化为如下求W的目标函数：

(6)求解(5)的目标函数可以获得W的更新公式如下：

其中I为单位阵，t表示迭代次数；

(7)固定其他未知数，可以获得如下的拉格朗日子问题：

该目标函数可以转化成的形式，其中，S＝J；其有如下的闭合解：

通过上述公式更新J；

(8)固定其他未知数，通过如下方式更新Eα：

(9)上述(8)中目标函数可以分解为如下的M个子问题：

该目标函数也可以转换成的形式，其中，有如下的闭合解：

(10)更新拉格朗日乘子：

G^t+1＝G^t+μ(J^t+1-W^t+1)

(11)更新参数μ：μ＝min(ρμ,μmax)；

(12)检查是否满足以下收敛条件：

||J^t+1-W^t+1||∞<ε

其中，ε＝10^-8，当不满足上述收敛条件时，重复(5)-(12)，直至满足收敛条件。

5、根据每个子块位置的映射矩阵Wi，对每个测试人脸图像的各正方形块进行分类，分类公式如下：

其中，z表示一个测试样本，zⁱ表示测试人脸图像的像素i对应的正方形块的向量表示，label(zⁱ)表示zⁱ所属的类别标签，表示利用像素i处对应的映射矩阵Wi将zⁱ映射带其所对应的类别向量，并取类别向量中值最大的一项最为最终的类别标签。

6、识别每个测试人脸块的类别之后，通过投票的方法最终确定测试人脸图像所属的类别。

本发明基于半监督子块联合回归的单样本人脸识别方法，每块的分类可以并行操作，本发明方法对光照变化具有很强的鲁棒性，可以在不依赖于额外训练样本集的条件下仍然获得较好的性能，同时对光照、表情、遮挡、时间变化都具有很好的鲁棒性。

以上实施例仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明保护范围之内。