一种高精度亚像元位移产生方法与流程

本发明属于光学成像领域，涉及一种高精度亚像元位移产生方法。

背景技术：

对于成像系统来说，在探测器像元与成像距离一定的情况下，要提升分辨率，增大焦距或增加F#是最直接的选择。然而，焦距的增大必然引起系统口径、质量、体积与成本的增加以及研制难度的增大。F#的增大可以在高分辨与轻小型化之间找到平衡点，然而其所带来的静态传递函数MTF(Modulation Transfer Function)和信噪比的下降除了对成像品质带来影响之外，也对相机的研制加工水平提出了更高的要求。因此，在不改变成像系统的硬件配置，尤其是不改变光学系统形式以及探测器像素物理大小的前提下实现分辨率的提升就成为了一种高性价比技术手段，而亚像元成像技术就是代表之一。

2002年5月4日，由阿丽亚娜四号火箭成功发射的SPOT-5卫星是法国航天局设计，与比利时和瑞典合作完成的地球资源卫星SPOT系列中性能最优的一颗。该卫星轨道为太阳同步轨道，轨道高度为832km。相机采用折反射式光学系统，焦距580mm，CCD像元大小6.5um、线阵像元个数12000。法国国家空间技术研究中心(CNES)提出了一个全新的概念——亚像元成像处理技术。通过将两片12000个像元的线阵CCD封装在同一芯片内，并且两排线阵CCD的位置排布彼此错位半个像元，之后利用焦平面上两排彼此错位半个像素的线阵CCD使相机在同一瞬间拍摄两幅影像。由于两幅影像包含不同的信息，对其进行计算机处理就可以合成高分辨率影像，以此使卫星相机的空间分辨率从5m提升至约3m。

2003年6月26日，OrbitView-3卫星发射成功，是由美国OrbitImage公司(轨道成像公司)所拥有的高分辨率商用光学卫星。卫星轨道为太阳同步轨道，轨道高度为470km，成像幅宽为8km，星载相机可以提供1m分辨率的全色影像和4m分辨率的多光谱影像。卫星焦平面的排布方式与SPOT-5卫星相似，也是由两排彼此错位半个像元的线阵CCD组成，获取的两幅低分辨率图像经过后续图像处理得到高分辨率图像数据。此外，由德国宇航中心研制的BIRD卫星红外遥感器HSRS(Hot Spot Recognition Sensors)和Leica公司的数字航空相机ADS40也采用了类似的亚像元采样超分辨重建技术实现分辨率的提升。

除了航天航空应用之外，亚像元成像技术也在工业相机以及消费数码相机领域开始得到应用。韩国Vieworks公司的VN系列像素位移相机专为超高分辨率拍摄静止物体而设计，也采用亚像元成像，其先进的像素位移技术是基于精确的压电位移控制。其产品系列中的VN-11MC相机能以9900万像素的高分辨率抓取图像，而VN-29MC相机可以达到更高的分辨率2亿6000万像素。同样，奥林巴斯公司在2015年的2月份发布的一款新的商用单反数码相机E-M5Mark II，也应用了亚像元超分辨重建技术。该相机在正常模式下可以实现1600万像素分辨率的成像，而进入超模式以后，可以在一次曝光中最多移动8次焦面并借此实现4000万像素甚至更高的分辨率成像效果。

尽管已经在高中低端领域得到了一定的应用，但是依然有大量的科研工作者在围绕亚像元成像技术开展理论研究工作，而如何产生高精度的具有亚像元位移量的序列图像对于超分辨重建算法的验证以及重建算法对亚像元位移控制精度偏差的敏感性研究至关重要。

由傅里叶变换的特性可知，如果图像在空间域产生一个平移，那么其所对应的傅里叶频谱就会被乘以一个与平移量有关的线性相位因子。因此，首先在傅里叶变换域对参考图像的频谱乘以一个由平移量构建的线性相位因子，之后利用傅里叶反变换就能够获得与参考图像之间相差确定平移量的另外一幅图像。基于傅里叶变换的平移变换其机理易于理解，不但能够产生整像素数目的像移，而且也能够产生亚像素级别的位移。然而研究表明，这种方式在产生亚像元位移时，其控制精度与图像行列的奇偶性，加窗是否得当等因素息息相关。在不加校正的情况下，这种方法产生的亚像元位移存在较大的偏差。

具体而言，基于傅里叶变换平移特性的亚像元产生模型是通过给参考图像的傅里叶频谱乘以一个与平移有关的线性相位因子，之后再对其进行傅里叶反变换就能够获得与参考图像具有相对位移量的新图像。这一过程的一维示例数学表达如下式所示：

其中，x_i代表参考图像的某一行(i＝0,1…L-1，L为一行的像素数目)；X_m为序列x_i的傅里叶频谱(m＝0,1…L-1)；k代表亚像素的位移量；y_m和Y_m分别代表与参考图像某一行x_i相比具有相对位移量k的新图像及其傅里叶频谱；FFT和FFT^-1分别代表正向傅里叶变换和傅里叶逆变换。

尽管基于傅里叶变换的亚像元位移产生模型物理意义明确，操作简便，但是研究表明，该模型在产生亚像元位移的时候通常存在一定的偏差。如果以实际输出的亚像元位移序列与理想位移序列之间的偏差的均方根误差作为评价依据，那么均方根误差通常都比较大，而且随着位移的增加变得更大。这一现象的存在对利用该方法精确模拟亚像元位移带来了较大的障碍。

技术实现要素：

为了解决利用傅里叶变换产生亚像元位移时存在的位移控制精度低的技术问题，本发明提供一种高精度亚像元位移产生方法。

本发明的技术解决方案是：一种高精度亚像元位移产生方法，其特殊之处在于：包括以下步骤：

1】位移初始化；

1.1】设定理想位移序列Si，其中i＝0,1,2…n；

1.2】以Si作为位移输入序列Xm，利用傅里叶变换产生具有相对位移的图像序列Ym，其中m＝0,1,2…n；

1.3】利用位移检测算法获得序列图像Ym中每一幅图像相对于初始图像的实际位移序列Si’；

1.4】计算实际位移序列Si’与理想位移序列Si之间的偏差均方根误差Ccost；

2】迭代计算偏差校正系数；

2.1】设定迭代次数iter和退火初始温度T，设定偏差校正系数初始值Di(i＝0,1,2…n)；

2.2】为当前的偏差校正系数Di增加扰动；

2.3】产生修正后的位移输入序列：Xm＝Xm+Di；利用傅里叶变换产生具有相对位移的图像序列Ym；

2.4】利用位移检测算法获得序列图像Ym中每一幅图像相对于初始图像的实际位移序列Si’；

2.5】计算实际位移序列Si’与理想位移序列Si之间的偏差均方根误差Ncost；

2.6】判断Ncost是否小于Ccost；若是，则执行步骤2.7】；若否，则执行步骤2.9】；

2.7】令Ccost＝Ncost，t＝t+1；

2.8】判断t是否大于iter；若是，则输出偏差校正系数Di，执行步骤3】；若否，则降低退火温度T并返回步骤2.2】；

2.9】计算接受率r＝exp((Ncost-Ccost)/T)，并判断r是否大于rand的当前值；若是，则执行步骤2.7】；若否，则执行步骤2.10】；其中，rand是可随机产生0～1之间的任意数值的随机函数；

2.10】令t＝t+1并判断t是否大于iter；若是，则输出偏差校正系数Di，执行步骤3】；若否，则降低退火温度T并返回步骤2.2】；

3】以Si+Di作为输入，产生接近理想位移序列Si的高精度亚像元位移。

降低退火温度T的方法是：令T＝ω*T，其中ω是一个大于0.9且小于1的常数。

偏差校正系数Di增加扰动的方法是：令Di＝Di+(-Δ+2Δ*(rand))；其中，0﹤Δ﹤0.1，rand是可随机产生0～1之间的任意数值的随机函数。

步骤3】中产生的高精度亚像元位移数值与理想位移序列Si之间的偏差均方根误差小于0.1像元。

本发明的有益效果在于：

(1)本发明将傅里叶变换亚像元位移产生与位相相关亚像素精度位移检测嵌入到模拟退火算法全局优化框架中，通过迭代搜索获得用于校正亚像素位移产生偏差的系数，以此来提升傅里叶变换模型所产生的亚像元位移精度。

(2)本发明通过获取偏差校正系数可以大幅提升亚像元位移序列的产生精度，使后期研究超分辨重建算法以及位移控制偏差对重建效果的影响有高精度仿真数据作为保证。

附图说明

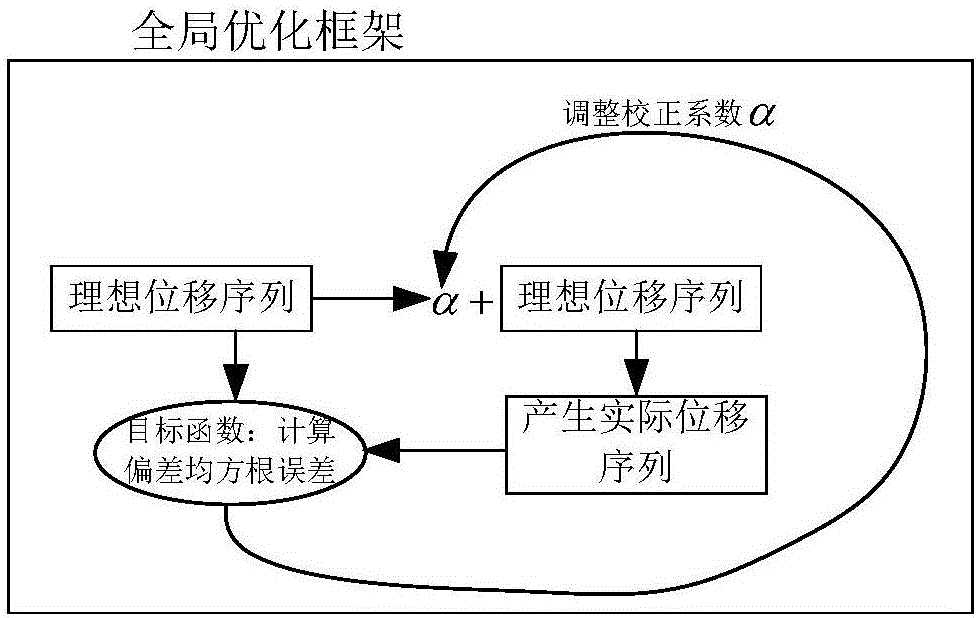
图1为本发明所提出的亚像元位移产生方法的基本原理示意图。

图2为产生高精度亚像元位移的较佳方法流程图。

图3为第一组实验模拟结果示意图；

图4为第二组实验模拟结果示意图；

图5为第三组实验模拟结果示意图；

图6为第四组实验模拟结果示意图；

具体实施方式

本发明所提出的方法是，通过将偏差校正系数作为待求解的变量，以理想位移序列与实际输出的位移序列之间的偏差均方根误差作为目标函数，利用全局优化在高维空间中搜索来获得最优的偏差校正系数，基本流程如图1所示。

在图2中，给出了由傅里叶变换亚像元位移生成模块与高精度的亚像元位移检测模块所组成的最优偏差校正系数生成算法流程。两者作为核心计算单元，在模拟退火全局优化算法框架的支持下通过不断迭代并最终收敛到最优的偏差校正系数。其中，高精度的亚像元位移检测模块采用经典位相相关算法，该算法具有优于0.5个像元的位移检测精度。

之所以采用模拟退火作为获得最优亚像元位移偏差校正系数的框架，是因为模拟退火方法是一种已经被证明的能够以概率1收敛于全局最优的优化方法，物理意义清晰，使用简单，应用非常广泛。模拟退火方法最大的特点在于，允许以动态计算的概率来接受中间迭代过程产生的劣解，从而帮助方法从局部极值中跳出。

模拟退火算法的运作流程由以下六个步骤组成：

第一、初始化。给定温度T的变化范围，并对其进行初始化，对解S进行初始化，并计算初始化解S所对应的当前目标函数值E(S)——这是模拟退火算法迭代的起点。

第二、设置一个整数t用来记录每一温度T下迭代已进行的次数，在每一温度T下，循环t次第三～第六步。

第三、产生一个新的解S’，根据目标函数分别计算当前解S和新解S’所对应的E(S)和E(S’)，并计算增量ΔE＝E(S’)-E(S)。

第四、如果ΔE<0，则新解S’替代当前解S作为当前的新解，新解对应的E(S’)作为新的当前目标函数值；如果ΔE>0，则需要计算新解的接受率r＝exp(-ΔE/kT)，若结果r>rand，则可以接受S’作为新的当前解，这里说得rand为一个自动生成介于[0，1]之间的随机数。

第五、如果迭代满足终止条件，则输出当前解作为最有解。终止条件通常取已设定的迭代次数或连续若干个新解都没有被接受或温度达到终止条件。

第六、逐渐减低温度控制参数T。如果T依然大于0，则转至第二步继续进行，直至满足终止条件为止。

模拟退火算法的全局搜索性能与退火速度(温度降低策略)以及以当前解为基础的产生临时新解的扰动机制密切相关。

首先，常见的温度控制策略有对数降温策略、快速降温策略、直线降温策略以及指数降温策略四种。温度下降过快，可能错过极值点；温度下降过慢，则会大大降低算法的收敛速度。在四种降温策略中，由于指数降温策略中温度的降低较有规律，所以这里采用指数降温策略，即如图2中所给出的T＝ωT，其中ω是一个接近于1的小数。

其次，按照特定的机制以当前解为基础产生新解是模拟退火算法得以迭代下去的关键。通常，随机地将微量的扰动叠加到当前解上来产生新的解，但是需要注意的是：扰动强度过大，有可能使算法的进程出现反复；扰动强度过小，算法可能需要花费很长的时间才能跳出局部极值。本发明中，选取扰动量(-Δ+2Δ*(rand))(其中Δ位于0～0.1之间，rand代表可随机产生0～1之间的任意数值的随机函数)可以很好地兼顾搜索速度与搜索的准确性。

图3～图6给出了四组典型的实施示例，用以证明本发明所提出的仿真模型在提升位移输出精度方面的能力。其中，每一幅图的(a)对应于未引入全局优化时理想位移与实际位移之间的偏差，而(b)则对应于引入全局优化以后的位移输出的改善情况。

在图3中，理想的拟产生的位移序列为0～1.5个像素，间隔0.15个像素。可以看到，未引入全局优化时，x和y方向上实际输出的位移序列与理想位移序列之间均具有较大的偏差，偏差均方根误差分别为0.8597和0.9609。在引入全局优化以后，x方向上实际输出的位移序列与理想位移序列之间的偏差显著减小，偏差均方根误差下降到约0.0599的水平；而y方向的改善略小，偏差均方根误差约为0.1左右。

在图4中，理想的拟产生的位移序列为0～2个像素，间隔0.2个像素。可以看到，未引入全局优化时，x和y方向上实际输出的位移序列与理想位移序列之间均具有较大的偏差，偏差均方根误差分别为1.2253和1.3811。在引入全局优化以后，x方向上实际输出的位移序列与理想位移序列之间的偏差显著减小，偏差均方根误差下降到约0.0592的水平；而y方向的改善略小，偏差均方根误差约为0.1左右。

在图5中，理想的拟产生的位移序列为0～3个像素，间隔0.3个像素。可以看到，未引入全局优化时，x和y方向上实际输出的位移序列与理想位移序列之间均具有较大的偏差，偏差均方根误差分别为1.9073和1.9985。在引入全局优化以后，x方向上实际输出的位移序列与理想位移序列之间的偏差显著减小，偏差均方根误差下降到约0.0671的水平；而y方向的改善略小，偏差均方根误差约为0.098左右。

在图6中，理想的拟产生的位移序列为0～5个像素，间隔0.5个像素。可以看到，未引入全局优化时，x和y方向上实际输出的位移序列与理想位移序列之间均具有较大的偏差，偏差均方根误差分别为3.3928和3.3589。在引入全局优化以后，x方向上实际输出的位移序列与理想位移序列之间的偏差显著减小，偏差均方根误差下降到约0.0840的水平；而y方向的改善略小，偏差均方根误差约为0.095左右。

由图3～图6可知，本发明所提出的仿真模型所产生的位移序列要更加接近于理想数值，即偏差均方根误差更小。x方向位移控制精度的提升要好于y方向，但是偏差的均方根误差均小于0.1，与为引入全局优化的数值相比大幅提高。